13.1.2平方根
图片预览









文档简介
课件31张PPT。13.1.2 算术平方根莆田南门学校 八年(3)(5)班 一个正数x的平方等于a,即 x2= a,这个正数x叫做a的算术平方根读作“根号a”x2 = a (x为正数)规定0的算术平方根是0,记作被开方数a≥01、什么是算术平方根30.110-3461.251.填空:1313±1.41.41.4±1112.下列说法错误的是( )A.(-3)2的算术平方根是3B.(-3)2的算术平方根是-3C.-(-16)的算术平方根是4D. |-4|的算术平方根是2E. 72的算术平方根是7F. -72的算术平方根是-7G. 5是25的算术平方根H.(-2)4 的算术平方根是8BFH3.计算 16270.0420058归纳无限不循环小数有限小数无限不循环小数无限不循环小数有限小数巩固 你能举出一些无限不循环小数
的例子吗? 下列各数是无限不循环小数吗?有限小数0.252.57.91250.79179.1250从运算结果可以发现:被开方数扩大(缩小)100倍,
它的算术平方根扩大(缩小)10倍.解:巩固5、已知 , ,
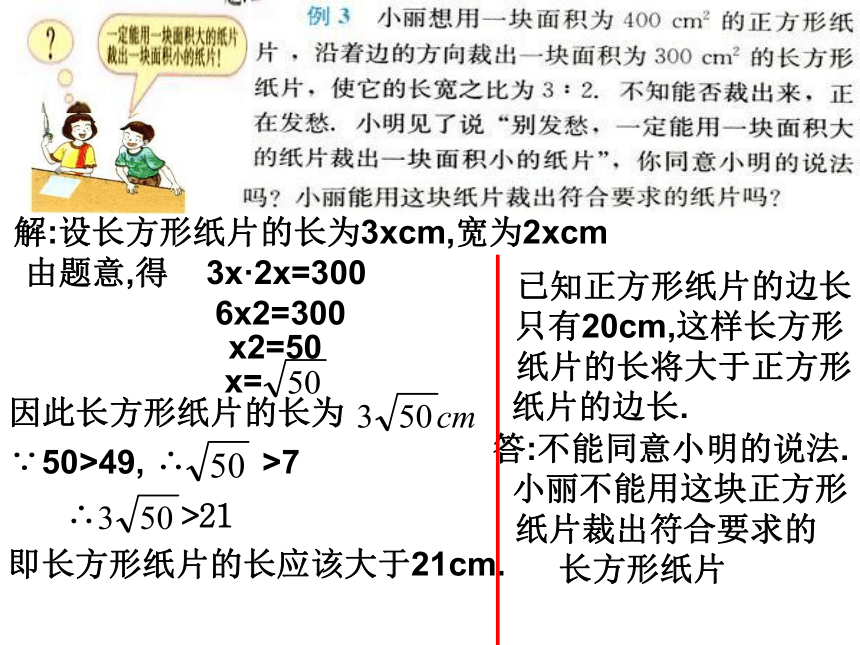
求 、 的值。解:设长方形纸片的长为3xcm,宽为2xcm由题意,得 3x·2x=300 6x2=300 x2=50即长方形纸片的长应该大于21cm. 已知正方形纸片的边长
只有20cm,这样长方形
纸片的长将大于正方形
纸片的边长. 答:不能同意小明的说法.
小丽不能用这块正方形
纸片裁出符合要求的
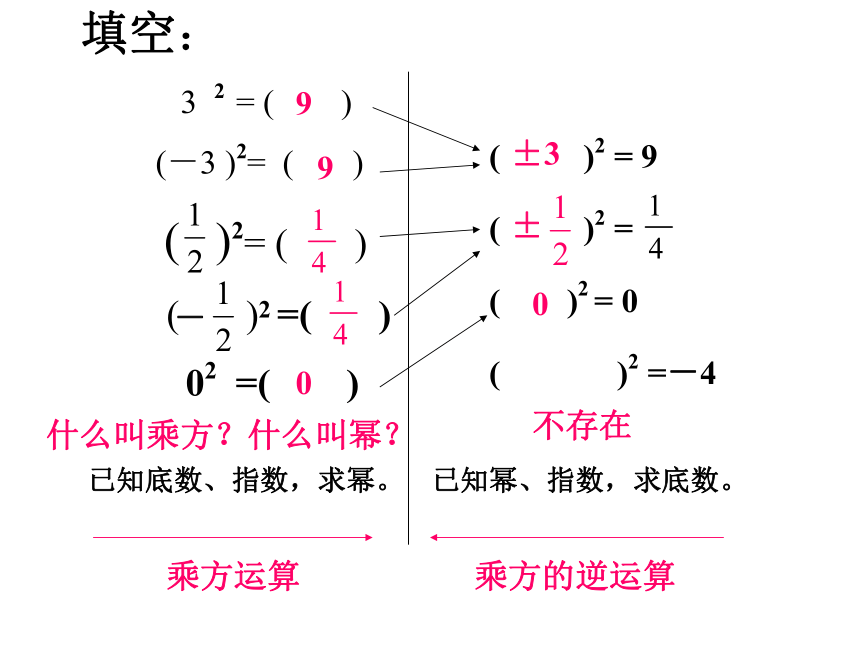
长方形纸片±0.8±3±4±1±6±7?X2 =9这个数X是多少?X2=a,这个数X是多少?已知底数、指数,求幂。已知幂、指数,求底数。( )2 = 9
( )2 =
( )2 = 0
( )2 =-4填空:
3 2 = ( )
(-3 )2= ( )
( )2= ( )
( )2 =( )
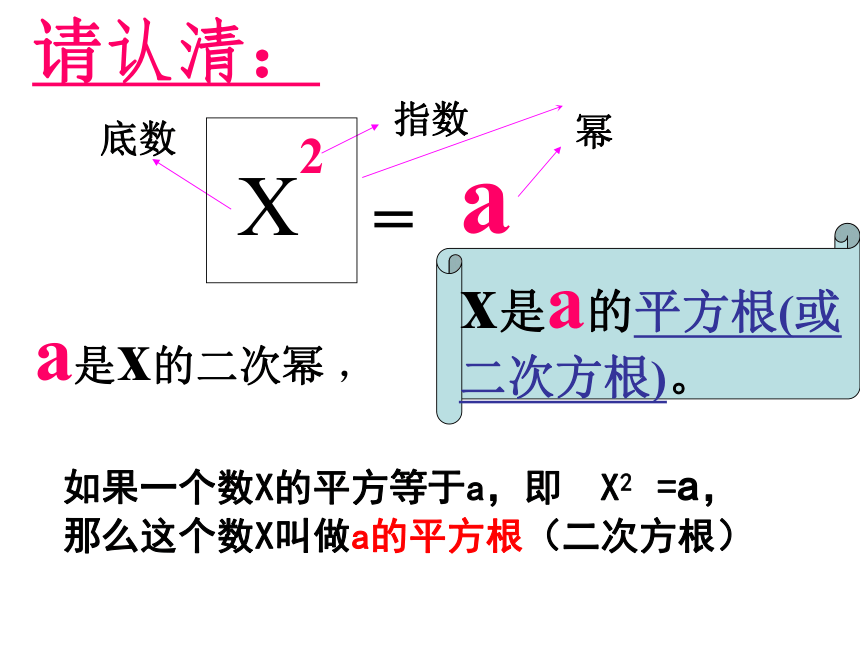
02 =( )990±30不存在乘方运算乘方的逆运算什么叫乘方?什么叫幂?请认清: a是x的二次幂 ,x是a的平方根(或二次方根)。如果一个数X的平方等于a,即 X2 =a,
那么这个数X叫做a的平方根(二次方根)如果一个数X的平方等于a,即 X2 = a,
那么这个数X叫做a的平方根(二次方根)a的平方根表示为x2 = a求数a的平方根的运算叫做开平方求一个数a的平方根的运算,叫做开平方。149+1-1+2-2+3-3149+1-1+2-2+3-3开平方平方±63±2得出:( )2 = 9
( )2 =
( )2 = 0
( )2 =-4
3 2 = ( )
(-3 )2= ( )
( )2= ( )
( )2 =( )
02 =( )990±30不存在请同学们概括一个数的平方根的性质:一个正数有两个平方根,它们互为相
反数;零有一个平方根,它是零本身;
负数没有平方根。
正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。a的一个平方根是3,则另一个平方根是 ,a= 。-393a-22和2a-3是m的两个平方根,
试求m的值。解:由题意得:3a-22=-(2a-3)
解得:a=5
∴3a-22=3×5-22=-7
∴m=49开平方:
求一个数a(a≥0)的平方根的运算,叫做开平
方,开平方运算是已知指数和幂,求底数。是不是所有的数都能进行开平方运算?不是,只有正数和零才能进行开平方运算。 由于平方与开平方互为逆运算,因此可以通过
平方运算来求一个数的平方根,也可以通过平方运
算来检验一个数是不是另一个数的平方根。复习3、面积为9的正方形的边长是 。5、如果 ,那么x = 。4、如果 ,那么x = 。例:估计大小小数部分=原数-整数部分探究你能比较下列两个数的大小吗?与与化根号法估算法作业1、比较大小: (1) 与 (2) 与1、知识方面:这节课我们学习了平方根的概念、表 示方法、求法及平方根的性质。
2、思维方法:平方运算和开平方运算互为逆运算,可以互相检验。
3、探究策略:由特殊到一般,再由一般到特殊,是发现问题和解决问题的基本方法和途径。
4、用定义解决问题也是的常用方法和有力工具。
本节课你学习了哪些知识?在 探索知识的过程中,你用了哪些方法?对你今后的学习有什么帮助?探究:4或-2a≤21、老师出了一道题:化简 。
同学甲马上解出结果为:
同学乙想了想,说甲解错了。你有什么
看法?补充练习;213256≥0-5互为相反数思考: 你能求出下列各式中的未知数x吗?
(1) 3x2-6.75=0(2)(x-1)2=4解: (1) x2=2.25
(2) x-1=±2
(3) x=49 (4) x-1=9
∴x=10∴x=±1.5 ∴x=3或x=-1 我们已学习了3种非负数,即绝对值、偶数次方、算术平方根。几个非负数的和为零,它们就同时为零,然后转化为方程(或方程组)来解。例:估计大小小数部分=原数-整数部分再见
的例子吗? 下列各数是无限不循环小数吗?有限小数0.252.57.91250.79179.1250从运算结果可以发现:被开方数扩大(缩小)100倍,
它的算术平方根扩大(缩小)10倍.解:巩固5、已知 , ,
求 、 的值。解:设长方形纸片的长为3xcm,宽为2xcm由题意,得 3x·2x=300 6x2=300 x2=50即长方形纸片的长应该大于21cm. 已知正方形纸片的边长
只有20cm,这样长方形
纸片的长将大于正方形
纸片的边长. 答:不能同意小明的说法.
小丽不能用这块正方形
纸片裁出符合要求的
长方形纸片±0.8±3±4±1±6±7?X2 =9这个数X是多少?X2=a,这个数X是多少?已知底数、指数,求幂。已知幂、指数,求底数。( )2 = 9
( )2 =
( )2 = 0
( )2 =-4填空:
3 2 = ( )
(-3 )2= ( )
( )2= ( )
( )2 =( )
02 =( )990±30不存在乘方运算乘方的逆运算什么叫乘方?什么叫幂?请认清: a是x的二次幂 ,x是a的平方根(或二次方根)。如果一个数X的平方等于a,即 X2 =a,
那么这个数X叫做a的平方根(二次方根)如果一个数X的平方等于a,即 X2 = a,
那么这个数X叫做a的平方根(二次方根)a的平方根表示为x2 = a求数a的平方根的运算叫做开平方求一个数a的平方根的运算,叫做开平方。149+1-1+2-2+3-3149+1-1+2-2+3-3开平方平方±63±2得出:( )2 = 9
( )2 =
( )2 = 0
( )2 =-4
3 2 = ( )
(-3 )2= ( )
( )2= ( )
( )2 =( )
02 =( )990±30不存在请同学们概括一个数的平方根的性质:一个正数有两个平方根,它们互为相
反数;零有一个平方根,它是零本身;
负数没有平方根。
正数有2个平方根,它们互为相反数;
0的平方根是0;
负数没有平方根。a的一个平方根是3,则另一个平方根是 ,a= 。-393a-22和2a-3是m的两个平方根,
试求m的值。解:由题意得:3a-22=-(2a-3)
解得:a=5
∴3a-22=3×5-22=-7
∴m=49开平方:
求一个数a(a≥0)的平方根的运算,叫做开平
方,开平方运算是已知指数和幂,求底数。是不是所有的数都能进行开平方运算?不是,只有正数和零才能进行开平方运算。 由于平方与开平方互为逆运算,因此可以通过
平方运算来求一个数的平方根,也可以通过平方运
算来检验一个数是不是另一个数的平方根。复习3、面积为9的正方形的边长是 。5、如果 ,那么x = 。4、如果 ,那么x = 。例:估计大小小数部分=原数-整数部分探究你能比较下列两个数的大小吗?与与化根号法估算法作业1、比较大小: (1) 与 (2) 与1、知识方面:这节课我们学习了平方根的概念、表 示方法、求法及平方根的性质。
2、思维方法:平方运算和开平方运算互为逆运算,可以互相检验。
3、探究策略:由特殊到一般,再由一般到特殊,是发现问题和解决问题的基本方法和途径。
4、用定义解决问题也是的常用方法和有力工具。
本节课你学习了哪些知识?在 探索知识的过程中,你用了哪些方法?对你今后的学习有什么帮助?探究:4或-2a≤21、老师出了一道题:化简 。
同学甲马上解出结果为:
同学乙想了想,说甲解错了。你有什么
看法?补充练习;213256≥0-5互为相反数思考: 你能求出下列各式中的未知数x吗?
(1) 3x2-6.75=0(2)(x-1)2=4解: (1) x2=2.25
(2) x-1=±2
(3) x=49 (4) x-1=9
∴x=10∴x=±1.5 ∴x=3或x=-1 我们已学习了3种非负数,即绝对值、偶数次方、算术平方根。几个非负数的和为零,它们就同时为零,然后转化为方程(或方程组)来解。例:估计大小小数部分=原数-整数部分再见
