13.2.1立方根
图片预览





文档简介
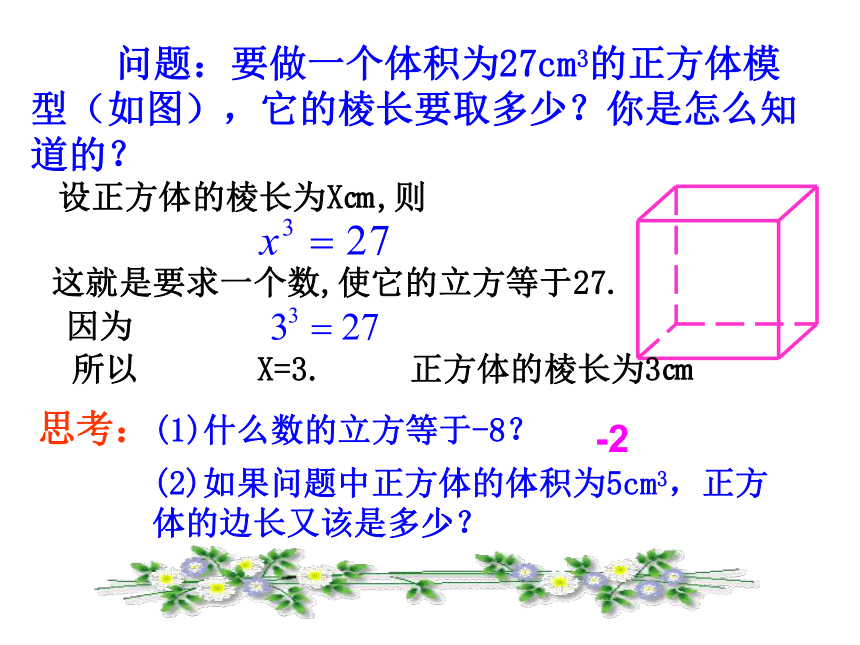
课件24张PPT。13.2.1 立方根莆田南门学校 八年(3)(5)班 问题:要做一个体积为27cm3的正方体模型(如图),它的棱长要取多少?你是怎么知道的?
思考:(1)什么数的立方等于-8?
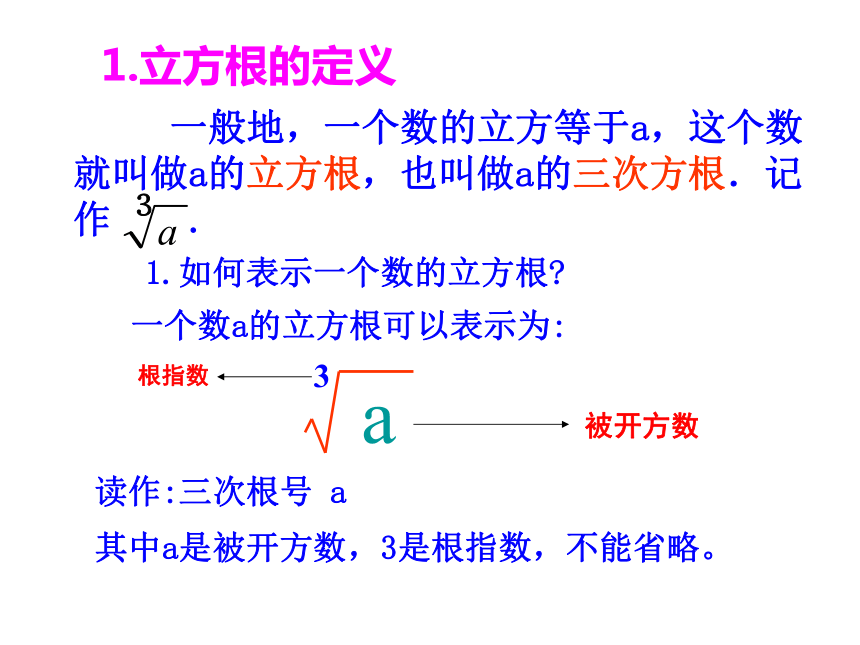
(2)如果问题中正方体的体积为5cm3,正方体的边长又该是多少?设正方体的棱长为X㎝,则这就是要求一个数,使它的立方等于27.因为 所以 X=3. 正方体的棱长为3㎝-21.立方根的定义1.如何表示一个数的立方根?一个数a的立方根可以表示为:根指数被开方数其中a是被开方数,3是根指数,不能省略。读作:三次根号 a思考:如果正方体的体积为5cm3,正方体的边长又该是多少?设正方体的边长为X,则 2.求一个数的立方根的运算,叫做开立方立方开立方互逆到现在我们学了几种运算?+,-,x,÷,乘方,开方(开平方,开立方)例1 求下列各数的立方根(1) 27 (2)-27 (3) (4)-0.064 (5) 0解:(1)∵ ∴27的立方根是3即(2)∵
∴-27的立方根是-3即(3)∵3(4) -0.064
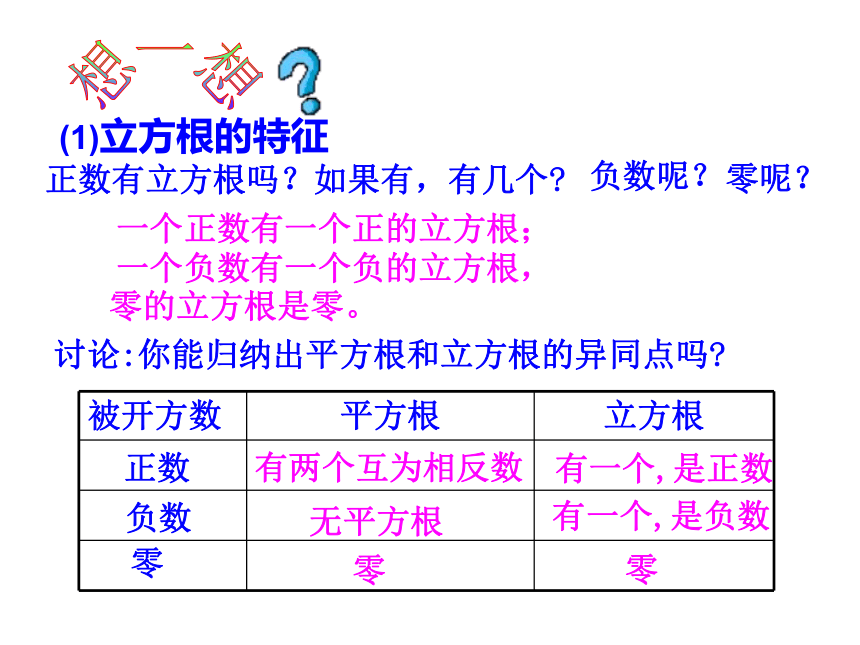
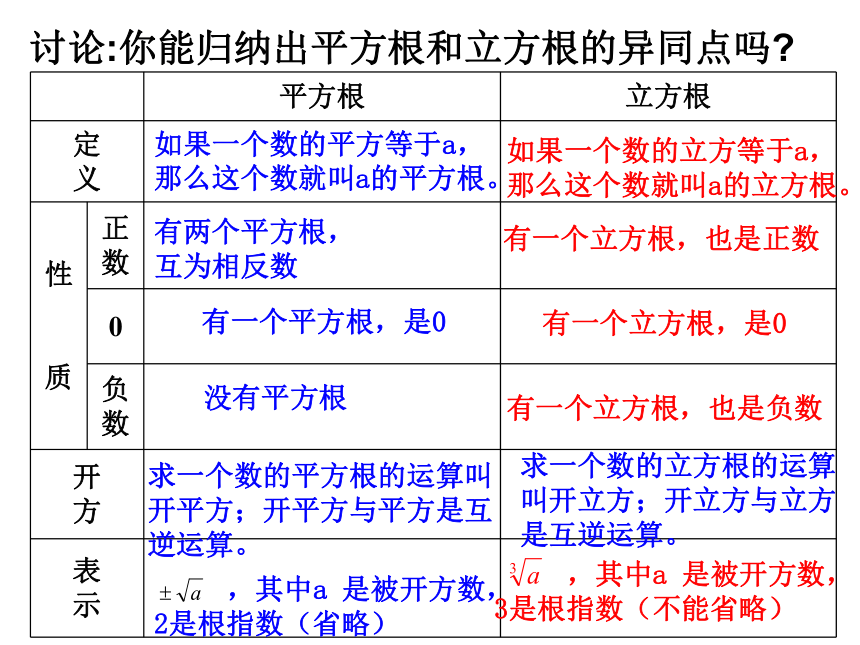
∴-0.064的立方根是-0.4∴0的立方根是0解∵(5) 02.立方根的性质探究1. 根据立方根的意义填空. 因为 =8,所以8的立方根是( ) 因为( ) =0.125,所以0.125的立方是( )因为( ) =0,所以0的立方根是( )因为 ( ) =-8,所以-8的立方根是( )因为( ) =- ,所以- 的立方( ) 02-20-2你能看出正数,0,负数的立方根各有什么特点?正数有立方根吗?如果有,有几个?想一想负数呢?零呢?一个正数有一个正的立方根;一个负数有一个负的立方根,零的立方根是零。(1)立方根的特征讨论:你能归纳出平方根和立方根的异同点吗?有两个互为相反数有一个,是正数无平方根零有一个,是负数零正数负数零如果一个数的平方等于a,
那么这个数就叫a的平方根。 如果一个数的立方等于a,
那么这个数就叫a的立方根。 有两个平方根,
互为相反数 有一个平方根,是0 没有平方根 求一个数的平方根的运算叫开平方;开平方与平方是互逆运算。 ,其中a 是被开方数,
2是根指数(省略) 求一个数的立方根的运算
叫开立方;开立方与立方
是互逆运算。 有一个立方根,也是负数 有一个立方根,是0 有一个立方根,也是正数 ,其中a 是被开方数,
3是根指数(不能省略) 讨论:你能归纳出平方根和立方根的异同点吗?练一练1.判断下列说法是否正确,并说明理由x(2) 25的平方根是5x(3) -64没有立方根x(4) -4的平方根是x(5) 0的平方根和立方根都是0√立方根是它本身的数有那些?有1, -1, 0平方根是它本身的数呢?只有0想一想引伸探究2猜一猜:你能从上述问题中总结出互为相反数的两个数a与-a的立方根的关系吗?=-2-2=-3-3例:求下列各式的值解:归纳: 求一个负数的立方根,可以先求出这个负数绝对值的立方根,然后再取它的相反数.探究3先填写下表,再回答问题:0.010.1110100从上面表格中你发现什么?归纳: 被开方数扩大(缩小)1000倍时,它的立方根扩大(缩小)10倍.练习:请同学们完成教材第171页的第1题,第4题. 已知半径为r 的球,其体积 的计 算公式为 . 如果甲、乙两球 体积的比为1 :8,则甲、乙两球的半径比为 .Rr乙甲 5.跳一跳:1.1110600.622、一个正方体的水晶砖,体积为100cm3,
它的棱长大约在 ( )A、4㎝~5㎝之间C、6㎝~7㎝之间B、5cm~6cm之间D、7㎝~8㎝之间1、估计68的立方根的大小在( )A、2与3之间B、3与4之间C、4与5之间D、5与6之间CA课堂练习2:3.你能求出下列各式中的未知数x吗?
(1) x3=343 (2)(x-1)3=125解:∴x=7∴x-1=5
X=6(3)(4)∴X=66∴x=8
(1)1的平方根是______;立方根为______;算术平方根为_________.
(2)平方根是它本身的数是__________.
(3)立方根是其本身的数是___________.
(4)算术平方根是其本身的数是________.(5) 的立方根为 . (6) 的平方根为 . (7) 的立方根为 . 填空练习:±1110±1 , 01 , 0-2±2-2课堂小结相同点:
①0的平方根、立方根都有一个是0
②平方根、立方根都是开方的结果。
不同点:
①定义不同
②个数不同
③表示方法不同
④被开方数的取值范围不同1.立方根的定义,性质,计算.2.立方根与平方根的异同小结你有哪些收获?表示方法的取值性质≥正数的立方根是正数;负数的立方根是负数;0的立方根是0.负数没有平方根0的平方根是0;正数有两个平方根,它们是互为相反数;求一个数的平方根的运算叫开平方;开平方与平方是互逆运算。 开方求一个数的立方根的运算叫开立方;开立方与立方是互逆运算。 0.06993-324.6-0.150722803280003、下列各组数中互为相反数的一组是( )4、要使 成立,则a必须满足A( D ) 的整数部分是( ),小数部分是( ) 的整数部分是( ),小数部分是( )5.6、比较大小活学活用再见
思考:(1)什么数的立方等于-8?
(2)如果问题中正方体的体积为5cm3,正方体的边长又该是多少?设正方体的棱长为X㎝,则这就是要求一个数,使它的立方等于27.因为 所以 X=3. 正方体的棱长为3㎝-21.立方根的定义1.如何表示一个数的立方根?一个数a的立方根可以表示为:根指数被开方数其中a是被开方数,3是根指数,不能省略。读作:三次根号 a思考:如果正方体的体积为5cm3,正方体的边长又该是多少?设正方体的边长为X,则 2.求一个数的立方根的运算,叫做开立方立方开立方互逆到现在我们学了几种运算?+,-,x,÷,乘方,开方(开平方,开立方)例1 求下列各数的立方根(1) 27 (2)-27 (3) (4)-0.064 (5) 0解:(1)∵ ∴27的立方根是3即(2)∵
∴-27的立方根是-3即(3)∵3(4) -0.064
∴-0.064的立方根是-0.4∴0的立方根是0解∵(5) 02.立方根的性质探究1. 根据立方根的意义填空. 因为 =8,所以8的立方根是( ) 因为( ) =0.125,所以0.125的立方是( )因为( ) =0,所以0的立方根是( )因为 ( ) =-8,所以-8的立方根是( )因为( ) =- ,所以- 的立方( ) 02-20-2你能看出正数,0,负数的立方根各有什么特点?正数有立方根吗?如果有,有几个?想一想负数呢?零呢?一个正数有一个正的立方根;一个负数有一个负的立方根,零的立方根是零。(1)立方根的特征讨论:你能归纳出平方根和立方根的异同点吗?有两个互为相反数有一个,是正数无平方根零有一个,是负数零正数负数零如果一个数的平方等于a,
那么这个数就叫a的平方根。 如果一个数的立方等于a,
那么这个数就叫a的立方根。 有两个平方根,
互为相反数 有一个平方根,是0 没有平方根 求一个数的平方根的运算叫开平方;开平方与平方是互逆运算。 ,其中a 是被开方数,
2是根指数(省略) 求一个数的立方根的运算
叫开立方;开立方与立方
是互逆运算。 有一个立方根,也是负数 有一个立方根,是0 有一个立方根,也是正数 ,其中a 是被开方数,
3是根指数(不能省略) 讨论:你能归纳出平方根和立方根的异同点吗?练一练1.判断下列说法是否正确,并说明理由x(2) 25的平方根是5x(3) -64没有立方根x(4) -4的平方根是x(5) 0的平方根和立方根都是0√立方根是它本身的数有那些?有1, -1, 0平方根是它本身的数呢?只有0想一想引伸探究2猜一猜:你能从上述问题中总结出互为相反数的两个数a与-a的立方根的关系吗?=-2-2=-3-3例:求下列各式的值解:归纳: 求一个负数的立方根,可以先求出这个负数绝对值的立方根,然后再取它的相反数.探究3先填写下表,再回答问题:0.010.1110100从上面表格中你发现什么?归纳: 被开方数扩大(缩小)1000倍时,它的立方根扩大(缩小)10倍.练习:请同学们完成教材第171页的第1题,第4题. 已知半径为r 的球,其体积 的计 算公式为 . 如果甲、乙两球 体积的比为1 :8,则甲、乙两球的半径比为 .Rr乙甲 5.跳一跳:1.1110600.622、一个正方体的水晶砖,体积为100cm3,
它的棱长大约在 ( )A、4㎝~5㎝之间C、6㎝~7㎝之间B、5cm~6cm之间D、7㎝~8㎝之间1、估计68的立方根的大小在( )A、2与3之间B、3与4之间C、4与5之间D、5与6之间CA课堂练习2:3.你能求出下列各式中的未知数x吗?
(1) x3=343 (2)(x-1)3=125解:∴x=7∴x-1=5
X=6(3)(4)∴X=66∴x=8
(1)1的平方根是______;立方根为______;算术平方根为_________.
(2)平方根是它本身的数是__________.
(3)立方根是其本身的数是___________.
(4)算术平方根是其本身的数是________.(5) 的立方根为 . (6) 的平方根为 . (7) 的立方根为 . 填空练习:±1110±1 , 01 , 0-2±2-2课堂小结相同点:
①0的平方根、立方根都有一个是0
②平方根、立方根都是开方的结果。
不同点:
①定义不同
②个数不同
③表示方法不同
④被开方数的取值范围不同1.立方根的定义,性质,计算.2.立方根与平方根的异同小结你有哪些收获?表示方法的取值性质≥正数的立方根是正数;负数的立方根是负数;0的立方根是0.负数没有平方根0的平方根是0;正数有两个平方根,它们是互为相反数;求一个数的平方根的运算叫开平方;开平方与平方是互逆运算。 开方求一个数的立方根的运算叫开立方;开立方与立方是互逆运算。 0.06993-324.6-0.150722803280003、下列各组数中互为相反数的一组是( )4、要使 成立,则a必须满足A( D ) 的整数部分是( ),小数部分是( ) 的整数部分是( ),小数部分是( )5.6、比较大小活学活用再见
