13.3.1实数
图片预览







文档简介
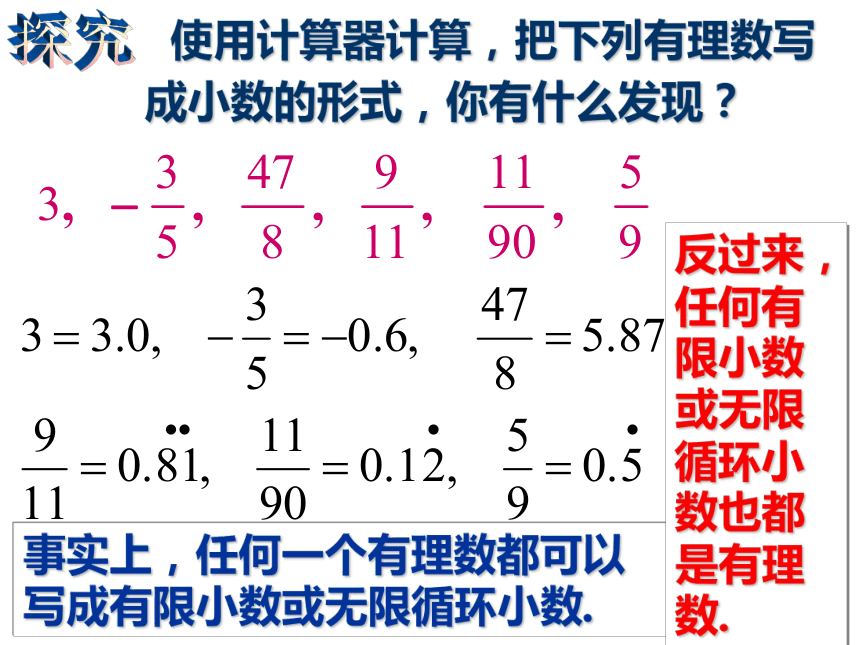
课件27张PPT。13.3.1 实数莆田南门学校 八年(3)(5)班 使用计算器计算,把下列有理数写成小数的形式,你有什么发现?探究事实上,任何一个有理数都可以写成有限小数或无限循环小数.反过来,任何有限小数或无限循环小数也都是有理数. 无限不循环的小数叫做无理数.你能举出一些无理数吗?无理数也有正负之分,例如:正无理数:
负无理数:——把下列各数分别填入相应的集合内: 有理数集合 无理数集合1.圆周率 及一些含有 的数2.开不尽方的数3.有一定的规律,但
不循环的无限小数。无理数的特征:注意:带根号的数不一定是无理数
有理数和无理数统称实数.无限不循环小数叫做无理数
( 强调: 无限 、 不循环.)
无理数常见的4种典型:注意:(3)、无限不循环小数:0.101001000…(两个
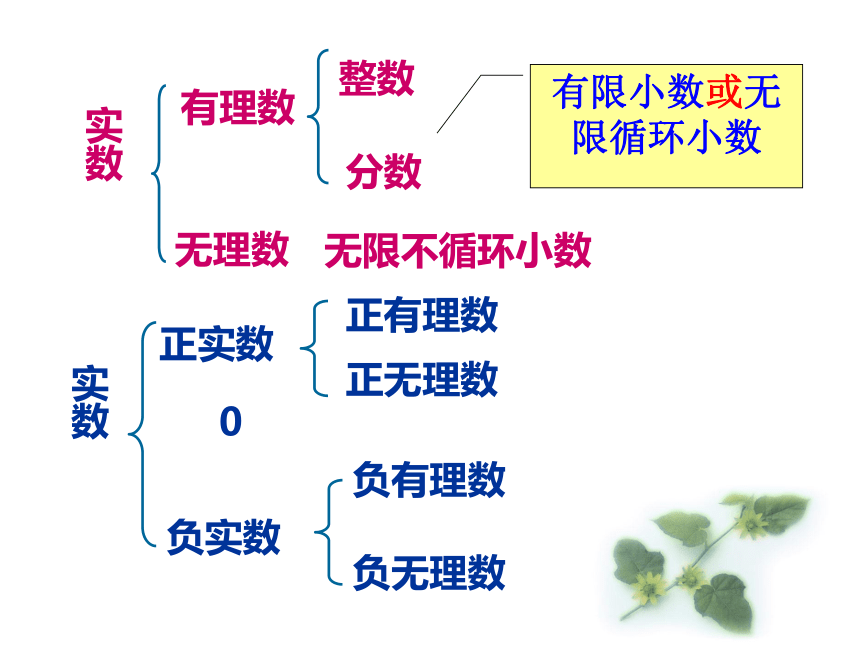
“1”之间依次多一个0)(4)、三角函数型:tan60°,sin45 °... 实数实数有理数无理数整数分数无限不循环小数正实数 0负实数正有理数正无理数负有理数负无理数有限小数或无限循环小数一、判断:1.实数不是有理数就是无理数。( )2.无理数都是无限不循环小数。( )3.无理数都是无限小数。( )4.带根号的数都是无理数。( )5.无理数一定都带根号。( )6.两个无理数之积不一定是无理数。( )7.两个无理数之和一定是无理数。( )×××8.有理数与无理数之和一定是无理数 ( )练一练把下列各数填入相应的集合内:(1)有理数集合:(2)无理数集合:(3)整数集合:(4)负数集合:(5)分数集合:(6)实数集合:每个有理数都可以用数轴上的点表示,那么无理数 是否也可以用数轴上的点来表示呢? 你能在数轴上找到表示 这样的无理数的点吗?π直径为1的圆(1)如下图,以单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正、负半轴的交点分别为点A和点B,数轴上A点和B点对应的数是什么?
(2)如果将所有有理数都标到数轴上,那么数轴 填满吗?BA每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一点都表示一个实数。即实数和数轴上的点是一一对应的。C在数轴上表示的两个实数,右边的数总比左边的数大。数轴上的点有些
表示有理数,有
些表示无理数. 在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。它本身0它的相反数练习2、填空:
(1) 的相反数是__________ (5) 绝对值是 _________ (2) 的倒数是____,(3)| |=___________(4)绝对值等于 的数是 _________ 的平方 是___ .二、填空5、在实数 中,
整数有
有理数有
无理数有
实数有它本身0它的相反数6.在实数范围内,下列判断正确的是( )
(A)若|x|=|y|,则x=y. (B)若x>y,则x2>y2.
(C)若|x|=( )2,则x=y. (D)若 ,则x=y5.在数轴上一个点到原点的距离为 ,则这个数点
表示的数为( )DD例.求下列各数的相反数、倒数、绝对值:若a、b互为相反数,c、d互为倒数,则1引入合并算术平方根性质乘法交换律
结合律范例例1、计算下列各式的值:(2)(1)注意:(1)计算题解题格式;(2)根指数、被开方数都分别相
同的无理数要合并。巩固1、计算:(1)(2)(3)范例例2、计算:(1)(2)注意:(1)先去括号、绝对值;(2)再合并。巩固2、计算:(1)(2)探究 例3、计算:(1) (精确到0.01)(2) (结果保留3个有效数字)注意:(1)无理数近似值多取1位;(2)结果按要求取近似值。巩固 3、计算:(1) (精确到0.01)(2) (保留3个有效数字)范例例4、解方程:(1)(2)注意:(1)将括号看作一个整体;(2)开平方有两个值,开立方只
有一个值。(3)巩固5、解方程:(1)(2)(3)2、(结果保留3个有效数字)注意:计算过程中要多保留一位!解:(3)原式=
===18.94≈18.9再见
负无理数:——把下列各数分别填入相应的集合内: 有理数集合 无理数集合1.圆周率 及一些含有 的数2.开不尽方的数3.有一定的规律,但
不循环的无限小数。无理数的特征:注意:带根号的数不一定是无理数
有理数和无理数统称实数.无限不循环小数叫做无理数
( 强调: 无限 、 不循环.)
无理数常见的4种典型:注意:(3)、无限不循环小数:0.101001000…(两个
“1”之间依次多一个0)(4)、三角函数型:tan60°,sin45 °... 实数实数有理数无理数整数分数无限不循环小数正实数 0负实数正有理数正无理数负有理数负无理数有限小数或无限循环小数一、判断:1.实数不是有理数就是无理数。( )2.无理数都是无限不循环小数。( )3.无理数都是无限小数。( )4.带根号的数都是无理数。( )5.无理数一定都带根号。( )6.两个无理数之积不一定是无理数。( )7.两个无理数之和一定是无理数。( )×××8.有理数与无理数之和一定是无理数 ( )练一练把下列各数填入相应的集合内:(1)有理数集合:(2)无理数集合:(3)整数集合:(4)负数集合:(5)分数集合:(6)实数集合:每个有理数都可以用数轴上的点表示,那么无理数 是否也可以用数轴上的点来表示呢? 你能在数轴上找到表示 这样的无理数的点吗?π直径为1的圆(1)如下图,以单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正、负半轴的交点分别为点A和点B,数轴上A点和B点对应的数是什么?
(2)如果将所有有理数都标到数轴上,那么数轴 填满吗?BA每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一点都表示一个实数。即实数和数轴上的点是一一对应的。C在数轴上表示的两个实数,右边的数总比左边的数大。数轴上的点有些
表示有理数,有
些表示无理数. 在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。它本身0它的相反数练习2、填空:
(1) 的相反数是__________ (5) 绝对值是 _________ (2) 的倒数是____,(3)| |=___________(4)绝对值等于 的数是 _________ 的平方 是___ .二、填空5、在实数 中,
整数有
有理数有
无理数有
实数有它本身0它的相反数6.在实数范围内,下列判断正确的是( )
(A)若|x|=|y|,则x=y. (B)若x>y,则x2>y2.
(C)若|x|=( )2,则x=y. (D)若 ,则x=y5.在数轴上一个点到原点的距离为 ,则这个数点
表示的数为( )DD例.求下列各数的相反数、倒数、绝对值:若a、b互为相反数,c、d互为倒数,则1引入合并算术平方根性质乘法交换律
结合律范例例1、计算下列各式的值:(2)(1)注意:(1)计算题解题格式;(2)根指数、被开方数都分别相
同的无理数要合并。巩固1、计算:(1)(2)(3)范例例2、计算:(1)(2)注意:(1)先去括号、绝对值;(2)再合并。巩固2、计算:(1)(2)探究 例3、计算:(1) (精确到0.01)(2) (结果保留3个有效数字)注意:(1)无理数近似值多取1位;(2)结果按要求取近似值。巩固 3、计算:(1) (精确到0.01)(2) (保留3个有效数字)范例例4、解方程:(1)(2)注意:(1)将括号看作一个整体;(2)开平方有两个值,开立方只
有一个值。(3)巩固5、解方程:(1)(2)(3)2、(结果保留3个有效数字)注意:计算过程中要多保留一位!解:(3)原式=
===18.94≈18.9再见
