《多项式与多项式相乘》教案
文档属性
| 名称 | 《多项式与多项式相乘》教案 |  | |
| 格式 | rar | ||
| 文件大小 | 20.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-05 22:23:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
《多项式与多项式相乘》教案
教学内容
本节课主要内容是探究多项式与多项式相乘的法则.
教学目标
1.知识与技能
让学生理解多项式乘以多项式的运算法则,能够按多项式乘法步骤进行简单的乘法运算.
2.过程与方法
经历探索多项式与多项式相乘的运算法则的推理过程,体会其运算的算理.
3.情感、态度与价值观
通过推理,培养学生计算能力,发展有条理的思考,逐步形成主动探索的习惯.
重、难点与关键
1.重点:多项式与多项式的乘法法则的理解及应用.
2.难点:多项式与多项式的乘法法则的应用.
3.关键:多项式的乘法应先转化为单项式与多项式相乘而后再应用已学过的运算法则解决.
教具准备
投影仪、硬纸片、剪刀.
教学方法
采用“情境──探索”教学方法,让学生在设置的情境中,通过操作感知多项式与多项式乘法的内涵.
教学过程
一、创设情境,操作感知
【动手操作】
首先,在你的硬纸板上用直尺画出一个矩形,并且分成如下图1所示的四部分,标上字母.
【学生活动】拿出准备好的硬纸板,画出上图1,并标上字母.
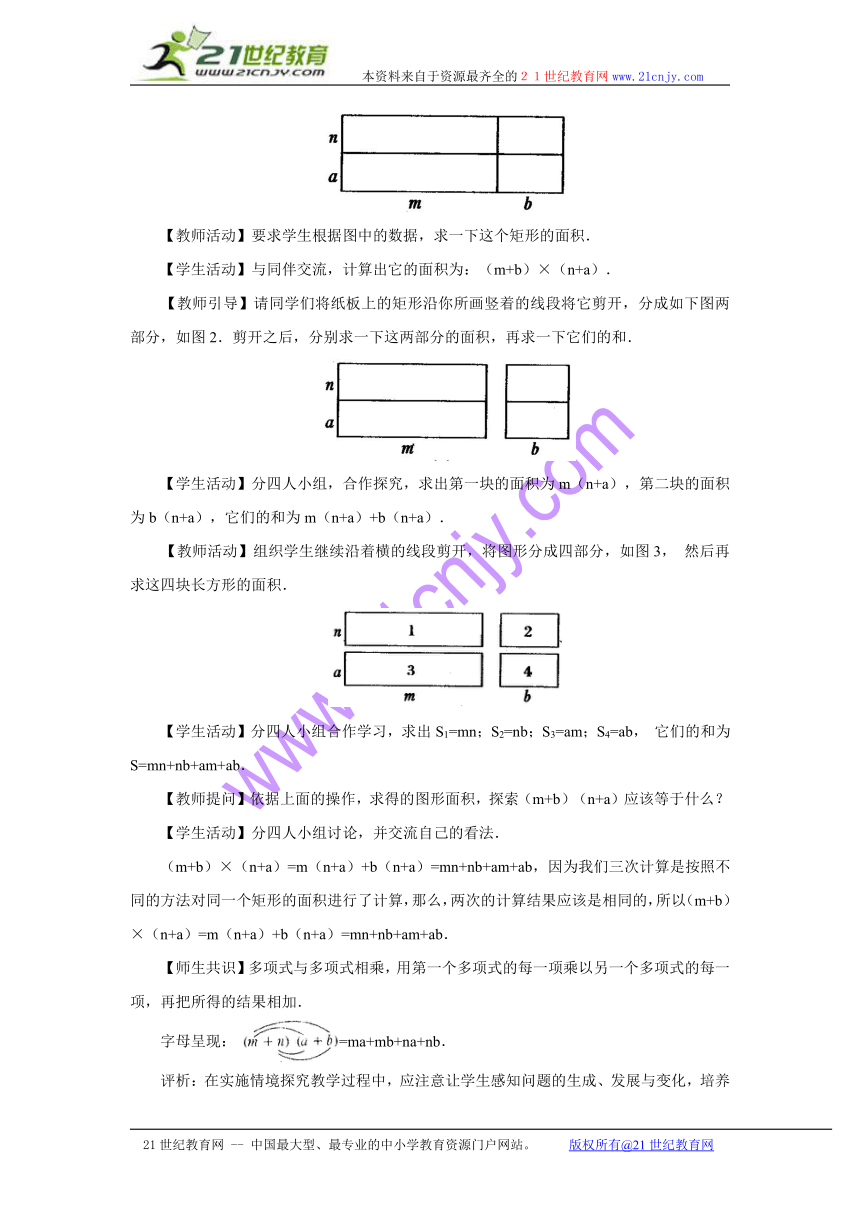
【教师活动】要求学生根据图中的数据,求一下这个矩形的面积.
【学生活动】与同伴交流,计算出它的面积为:(m+b)×(n+a).
【教师引导】请同学们将纸板上的矩形沿你所画竖着的线段将它剪开,分成如下图两部分,如图2.剪开之后,分别求一下这两部分的面积,再求一下它们的和.
【学生活动】分四人小组,合作探究,求出第一块的面积为m(n+a),第二块的面积为b(n+a),它们的和为m(n+a)+b(n+a).
【教师活动】组织学生继续沿着横的线段剪开,将图形分成四部分,如图3,然后再求这四块长方形的面积.
【学生活动】分四人小组合作学习,求出S1=mn;S2=nb;S3=am;S4=ab,它们的和为S=mn+nb+am+ab.
【教师提问】依据上面的操作,求得的图形面积,探索(m+b)(n+a)应该等于什么?
【学生活动】分四人小组讨论,并交流自己的看法.
(m+b)×(n+a)=m(n+a)+b(n+a)=mn+nb+am+ab,因为我们三次计算是按照不同的方法对同一个矩形的面积进行了计算,那么,两次的计算结果应该是相同的,所以(m+b)×(n+a)=m(n+a)+b(n+a)=mn+nb+am+ab.
【师生共识】多项式与多项式相乘,用第一个多项式的每一项乘以另一个多项式的每一项,再把所得的结果相加.
字母呈现: =ma+mb+na+nb.
评析:在实施情境探究教学过程中,应注意让学生感知问题的生成、发展与变化,培养学生善于发现的科学精神以及合作交流的精神和创新意识.
二、范例学习,应用所学
【例1】计算:
(1)(x+2)(x-3) (2)(3x-1)(2x+1)
【思路点拨】例1有两个特点:①两因式项数相同;②每个因式的项的最高次数都是1,应用多项式的乘法法则相乘时应注意x·x=x1+1=x2,还应注意符号.
【例2】计算:
(1)(x-3y)(x+7y) (2)(2x+5y)(3x-2y)
【思路点拨】教学中要强调多项式与多项式相乘的基本法则,提醒学生注意多项式的每一项都应该带上它前面的正负号.多项式是单项式的和,每一项都包括前面的符号,在计算时一定要注意确定积中各项的符号.
【例3】先化简,再求值:
(a-3b)2+(3a+b)2-(a+5b)2+(a-5b)2,其中a=-8,b=-6.
【思路点拨】本题碰到乘方的运算问题,应先将(a-3b)2转化为(a-3b)(a-3b),然后再运用多项式乘法法则进行计算.
【教师活动】操作投影仪,呈现例1~例3,启发学生参与到例题所设置的计算问题中去.
【学生活动】参与其中,领会多项式乘法的运用方法以及注意的问题.
三、随堂练习,巩固新知
课本P148练习第1、2题.
【探究时空】
一块长m米,宽n米的玻璃,长宽各裁掉a米后恰好能铺盖一张办公桌台面(玻璃与台面一样大小),问台面面积是多少?
四、课堂总结,发展潜能
1.多项式与多项式相乘,应充分结合导图中的问题来理解多项式与多项式相乘的结果,利用乘法分配律来理解(m+n)与(a+b)相乘的结果,导出多项式乘法的法则.
2.多项式与多项式相乘,第一步要先进行整理,在用一个多项式的每一项去乘另一个多项式的每一项时,要“依次”进行,不重复,不遗漏,且各个多项式中的项不能自乘,多项式是几个单项式的和,每一项都包括前面的符号,在计算时要正确确定积中各项的符号.
五、布置作业,专题突破
1.课本P149习题15.1第5、6、7(2)、9、10题.
2.选用第七课时作业设计.
板书设计
把黑板分成三份,左边部分板书多项式乘法法则,中间和右边部分板书例题.
疑难解析
计算:8x2-(x-2)(3x+1)-2(x+1)(x-5)
解法1:原式=8x2+(-1)(x-2)(3x+1)+(-2)(x+1)(x-5)
=8x2+(-1)(3x2-5x-2)+(-2)(x2-4x-5)
=8x2+(-3x2+5x+2)+(-2x2+8x+10)
=8x2-3x2+5x+2-2x2+8x+10
=3x2+13x+12.
解法2:原式=8x2+(-1)(x-2)(3x+1)+(-2)(x+1)(x-5)
=8x2+(-x+2)(3x+1)+(-2x-2)(x-5)
=8x2+(-3x2+5x+2)+(-2x2+8x+10)(以下略)
解法3:原式=8x2-[(x-2)(3x+1)]-[2(x+1)(x-5)]
=8x2-(3x2-5x-2)-[(2x+2)(x-5)]
=8x2-(3x2-5x-2)-(2x2-8x-10)(以下略)
从上述解答可以看出:当多项式相乘前面是负号时,处理负号可以采用以下方法:①将负号视为(-1)与之相乘(解法一和解法二均是这样处理);②将负号后面的多项式结合在一起先乘,然后利用去括号法则(如解法三的处理方法).
第七课时作业设计
一、选择题:
1.下列各式计算中,正确的是( ).
A.(x-1)(x+2)=x2-3x-2 B.(a-3)(a+2)=a2-a+6
C.(x+4)(x-5)=x2-20x-1 D.(x-3)(x-1)=x2-4x+3
2.计算(5x+2)(2x-1)的结果是( ).
A.10x2-2 B.10x2-x-2
C.10x2+4x-2 D.10x2-5x-2
3.以下计算:
(1)(x-y)(x-2y)=x2-3xy+2y2
(2)(1+2x)(1-2x)=1-4x+4x2
(3)(2a-3b)(2a+3b)=4a2-9b2
(4)(x+y)(2x-3y)=2x2-3xy+9y2中正确的有( )个.
A.1 B.2 C.3 D.4
二、计算.
4.(2x-3)(3x-4)
5.2(a-4)(a+3)-(2a+1)(a-3)
三、先化简再求值.
6.(x-2y)(x+3y)-2(x-y)(x-4y),其中x=-1,y=2.
7.(x-3)(x2-6x+1)-x(x2-x-3),其中x=-1.
四、解下列方程(组).
8.(x-2)(x-3)=(x+4)(x-1)-20
9.
答案:
一、1.D 2.B 3.B
二、4.6x2-17x+2 5.3a-21
三、6.-79 7.-33
四、8.x= 9.略
育星教育网 www. ( http: / / www.21cnjy.com / )
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
《多项式与多项式相乘》教案
教学内容
本节课主要内容是探究多项式与多项式相乘的法则.
教学目标
1.知识与技能
让学生理解多项式乘以多项式的运算法则,能够按多项式乘法步骤进行简单的乘法运算.
2.过程与方法
经历探索多项式与多项式相乘的运算法则的推理过程,体会其运算的算理.
3.情感、态度与价值观
通过推理,培养学生计算能力,发展有条理的思考,逐步形成主动探索的习惯.
重、难点与关键
1.重点:多项式与多项式的乘法法则的理解及应用.
2.难点:多项式与多项式的乘法法则的应用.
3.关键:多项式的乘法应先转化为单项式与多项式相乘而后再应用已学过的运算法则解决.
教具准备
投影仪、硬纸片、剪刀.
教学方法
采用“情境──探索”教学方法,让学生在设置的情境中,通过操作感知多项式与多项式乘法的内涵.
教学过程
一、创设情境,操作感知
【动手操作】
首先,在你的硬纸板上用直尺画出一个矩形,并且分成如下图1所示的四部分,标上字母.
【学生活动】拿出准备好的硬纸板,画出上图1,并标上字母.
【教师活动】要求学生根据图中的数据,求一下这个矩形的面积.
【学生活动】与同伴交流,计算出它的面积为:(m+b)×(n+a).
【教师引导】请同学们将纸板上的矩形沿你所画竖着的线段将它剪开,分成如下图两部分,如图2.剪开之后,分别求一下这两部分的面积,再求一下它们的和.
【学生活动】分四人小组,合作探究,求出第一块的面积为m(n+a),第二块的面积为b(n+a),它们的和为m(n+a)+b(n+a).
【教师活动】组织学生继续沿着横的线段剪开,将图形分成四部分,如图3,然后再求这四块长方形的面积.
【学生活动】分四人小组合作学习,求出S1=mn;S2=nb;S3=am;S4=ab,它们的和为S=mn+nb+am+ab.
【教师提问】依据上面的操作,求得的图形面积,探索(m+b)(n+a)应该等于什么?
【学生活动】分四人小组讨论,并交流自己的看法.
(m+b)×(n+a)=m(n+a)+b(n+a)=mn+nb+am+ab,因为我们三次计算是按照不同的方法对同一个矩形的面积进行了计算,那么,两次的计算结果应该是相同的,所以(m+b)×(n+a)=m(n+a)+b(n+a)=mn+nb+am+ab.
【师生共识】多项式与多项式相乘,用第一个多项式的每一项乘以另一个多项式的每一项,再把所得的结果相加.
字母呈现: =ma+mb+na+nb.
评析:在实施情境探究教学过程中,应注意让学生感知问题的生成、发展与变化,培养学生善于发现的科学精神以及合作交流的精神和创新意识.
二、范例学习,应用所学
【例1】计算:
(1)(x+2)(x-3) (2)(3x-1)(2x+1)
【思路点拨】例1有两个特点:①两因式项数相同;②每个因式的项的最高次数都是1,应用多项式的乘法法则相乘时应注意x·x=x1+1=x2,还应注意符号.
【例2】计算:
(1)(x-3y)(x+7y) (2)(2x+5y)(3x-2y)
【思路点拨】教学中要强调多项式与多项式相乘的基本法则,提醒学生注意多项式的每一项都应该带上它前面的正负号.多项式是单项式的和,每一项都包括前面的符号,在计算时一定要注意确定积中各项的符号.
【例3】先化简,再求值:
(a-3b)2+(3a+b)2-(a+5b)2+(a-5b)2,其中a=-8,b=-6.
【思路点拨】本题碰到乘方的运算问题,应先将(a-3b)2转化为(a-3b)(a-3b),然后再运用多项式乘法法则进行计算.
【教师活动】操作投影仪,呈现例1~例3,启发学生参与到例题所设置的计算问题中去.
【学生活动】参与其中,领会多项式乘法的运用方法以及注意的问题.
三、随堂练习,巩固新知
课本P148练习第1、2题.
【探究时空】
一块长m米,宽n米的玻璃,长宽各裁掉a米后恰好能铺盖一张办公桌台面(玻璃与台面一样大小),问台面面积是多少?
四、课堂总结,发展潜能
1.多项式与多项式相乘,应充分结合导图中的问题来理解多项式与多项式相乘的结果,利用乘法分配律来理解(m+n)与(a+b)相乘的结果,导出多项式乘法的法则.
2.多项式与多项式相乘,第一步要先进行整理,在用一个多项式的每一项去乘另一个多项式的每一项时,要“依次”进行,不重复,不遗漏,且各个多项式中的项不能自乘,多项式是几个单项式的和,每一项都包括前面的符号,在计算时要正确确定积中各项的符号.
五、布置作业,专题突破
1.课本P149习题15.1第5、6、7(2)、9、10题.
2.选用第七课时作业设计.
板书设计
把黑板分成三份,左边部分板书多项式乘法法则,中间和右边部分板书例题.
疑难解析
计算:8x2-(x-2)(3x+1)-2(x+1)(x-5)
解法1:原式=8x2+(-1)(x-2)(3x+1)+(-2)(x+1)(x-5)
=8x2+(-1)(3x2-5x-2)+(-2)(x2-4x-5)
=8x2+(-3x2+5x+2)+(-2x2+8x+10)
=8x2-3x2+5x+2-2x2+8x+10
=3x2+13x+12.
解法2:原式=8x2+(-1)(x-2)(3x+1)+(-2)(x+1)(x-5)
=8x2+(-x+2)(3x+1)+(-2x-2)(x-5)
=8x2+(-3x2+5x+2)+(-2x2+8x+10)(以下略)
解法3:原式=8x2-[(x-2)(3x+1)]-[2(x+1)(x-5)]
=8x2-(3x2-5x-2)-[(2x+2)(x-5)]
=8x2-(3x2-5x-2)-(2x2-8x-10)(以下略)
从上述解答可以看出:当多项式相乘前面是负号时,处理负号可以采用以下方法:①将负号视为(-1)与之相乘(解法一和解法二均是这样处理);②将负号后面的多项式结合在一起先乘,然后利用去括号法则(如解法三的处理方法).
第七课时作业设计
一、选择题:
1.下列各式计算中,正确的是( ).
A.(x-1)(x+2)=x2-3x-2 B.(a-3)(a+2)=a2-a+6
C.(x+4)(x-5)=x2-20x-1 D.(x-3)(x-1)=x2-4x+3
2.计算(5x+2)(2x-1)的结果是( ).
A.10x2-2 B.10x2-x-2
C.10x2+4x-2 D.10x2-5x-2
3.以下计算:
(1)(x-y)(x-2y)=x2-3xy+2y2
(2)(1+2x)(1-2x)=1-4x+4x2
(3)(2a-3b)(2a+3b)=4a2-9b2
(4)(x+y)(2x-3y)=2x2-3xy+9y2中正确的有( )个.
A.1 B.2 C.3 D.4
二、计算.
4.(2x-3)(3x-4)
5.2(a-4)(a+3)-(2a+1)(a-3)
三、先化简再求值.
6.(x-2y)(x+3y)-2(x-y)(x-4y),其中x=-1,y=2.
7.(x-3)(x2-6x+1)-x(x2-x-3),其中x=-1.
四、解下列方程(组).
8.(x-2)(x-3)=(x+4)(x-1)-20
9.
答案:
一、1.D 2.B 3.B
二、4.6x2-17x+2 5.3a-21
三、6.-79 7.-33
四、8.x= 9.略
育星教育网 www. ( http: / / www.21cnjy.com / )
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
