相似三角形的判定(一)导学稿
图片预览
文档简介
磁涧二中九年级数学导学稿
第22章 图形的相似 第五课时相似三角形的判定(一)
执笔人:梁希阳 审核人:姚小伟 使用时间:2010 年 月 日
导学目标:1、经历两个三角形相似的探索过程;
2、能说出识别两个三角形相似的方法:有两个角分别相等的两个三角形相似;
2、会用这种方法判断两个三角形是否相似。
导学重难点:掌握相似三角形的判定定理,并能熟练地运用时重点也是难点 。
导学过程:
一、想一想,填一填:
1、判定两个三角形全等有哪些方法;判定两个三角形相似是否一定要知道他们的对应角相等,对应角成比例呢?
二、学一学,做一做。
1、学习56—57页内容,解决下列问题:
(1)如果一个三角形的 角分别与另一个三角形的 角对应相等,那么这两个三角形相似.
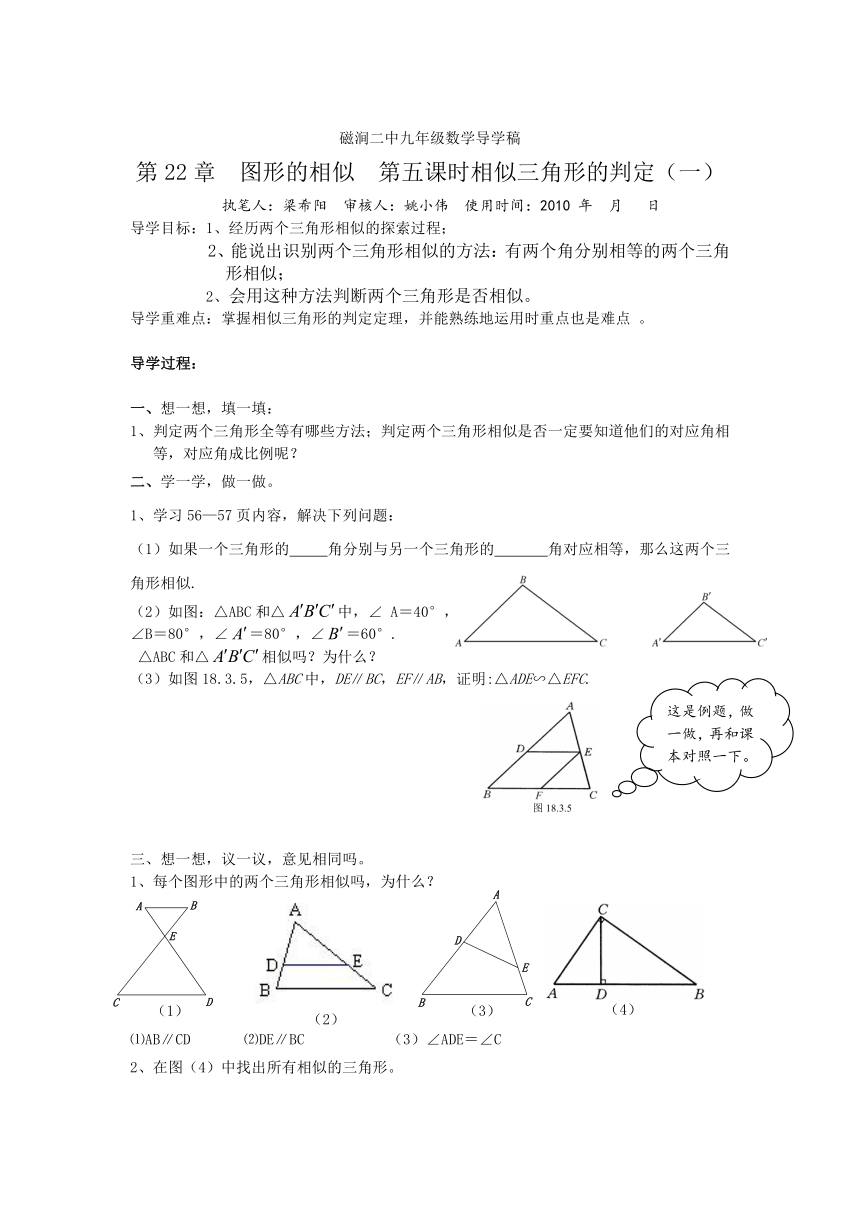
(2)如图:△ABC和△中,∠ A=40°,
∠B=80°,∠=80°,∠=60°.
△ABC和△相似吗?为什么?
(3)如图18.3.5,△ABC中,DE∥BC,EF∥AB,证明:△ADE∽△EFC.
三、想一想,议一议,意见相同吗。
1、每个图形中的两个三角形相似吗,为什么?
⑴AB∥CD ⑵DE∥BC (3)∠ADE=∠C
2、在图(4)中找出所有相似的三角形。
四、学完这节课,我知道了:
五、课堂测评:
1、下列各组三角形一定相似的是( )
A.两个直角三角形 B.两个钝角三角形 C.两个等腰三角形 D.两个等边三角形
2、△ABC的两个角分别是60°和72°,和△的两个角分别是
60°和48°,△ABC和△
3、如图,D是△ABC的边AC 上一点,连接BD,△ABC∽△BDC,则需
要添加的条件是
4、如图,E、F分别是△ABC的边BC上的点,DE∥AB,DF∥AC ,
求证:△ABC∽△DEF.
5、如图,已知△ABC与△ADE的边DE、AB相交于O,
且∠1=∠2=∠3.
(1) 试证明△ADO∽△EBO.
(2)证明△ADE∽△ABC.
这是例题,做一做,再和课本对照一下。
(1)
(2)
(3)
(4)
总结一下吧。
A
B
C
D
E
F
第4题
O
第5题
第22章 图形的相似 第五课时相似三角形的判定(一)
执笔人:梁希阳 审核人:姚小伟 使用时间:2010 年 月 日
导学目标:1、经历两个三角形相似的探索过程;
2、能说出识别两个三角形相似的方法:有两个角分别相等的两个三角形相似;
2、会用这种方法判断两个三角形是否相似。
导学重难点:掌握相似三角形的判定定理,并能熟练地运用时重点也是难点 。
导学过程:
一、想一想,填一填:
1、判定两个三角形全等有哪些方法;判定两个三角形相似是否一定要知道他们的对应角相等,对应角成比例呢?
二、学一学,做一做。
1、学习56—57页内容,解决下列问题:
(1)如果一个三角形的 角分别与另一个三角形的 角对应相等,那么这两个三角形相似.
(2)如图:△ABC和△中,∠ A=40°,
∠B=80°,∠=80°,∠=60°.
△ABC和△相似吗?为什么?
(3)如图18.3.5,△ABC中,DE∥BC,EF∥AB,证明:△ADE∽△EFC.
三、想一想,议一议,意见相同吗。
1、每个图形中的两个三角形相似吗,为什么?
⑴AB∥CD ⑵DE∥BC (3)∠ADE=∠C
2、在图(4)中找出所有相似的三角形。
四、学完这节课,我知道了:
五、课堂测评:
1、下列各组三角形一定相似的是( )
A.两个直角三角形 B.两个钝角三角形 C.两个等腰三角形 D.两个等边三角形
2、△ABC的两个角分别是60°和72°,和△的两个角分别是
60°和48°,△ABC和△
3、如图,D是△ABC的边AC 上一点,连接BD,△ABC∽△BDC,则需
要添加的条件是
4、如图,E、F分别是△ABC的边BC上的点,DE∥AB,DF∥AC ,
求证:△ABC∽△DEF.
5、如图,已知△ABC与△ADE的边DE、AB相交于O,
且∠1=∠2=∠3.
(1) 试证明△ADO∽△EBO.
(2)证明△ADE∽△ABC.
这是例题,做一做,再和课本对照一下。
(1)
(2)
(3)
(4)
总结一下吧。
A
B
C
D
E
F
第4题
O
第5题
