新博初中九年级数学22.4-22.5测验题
文档属性
| 名称 | 新博初中九年级数学22.4-22.5测验题 | 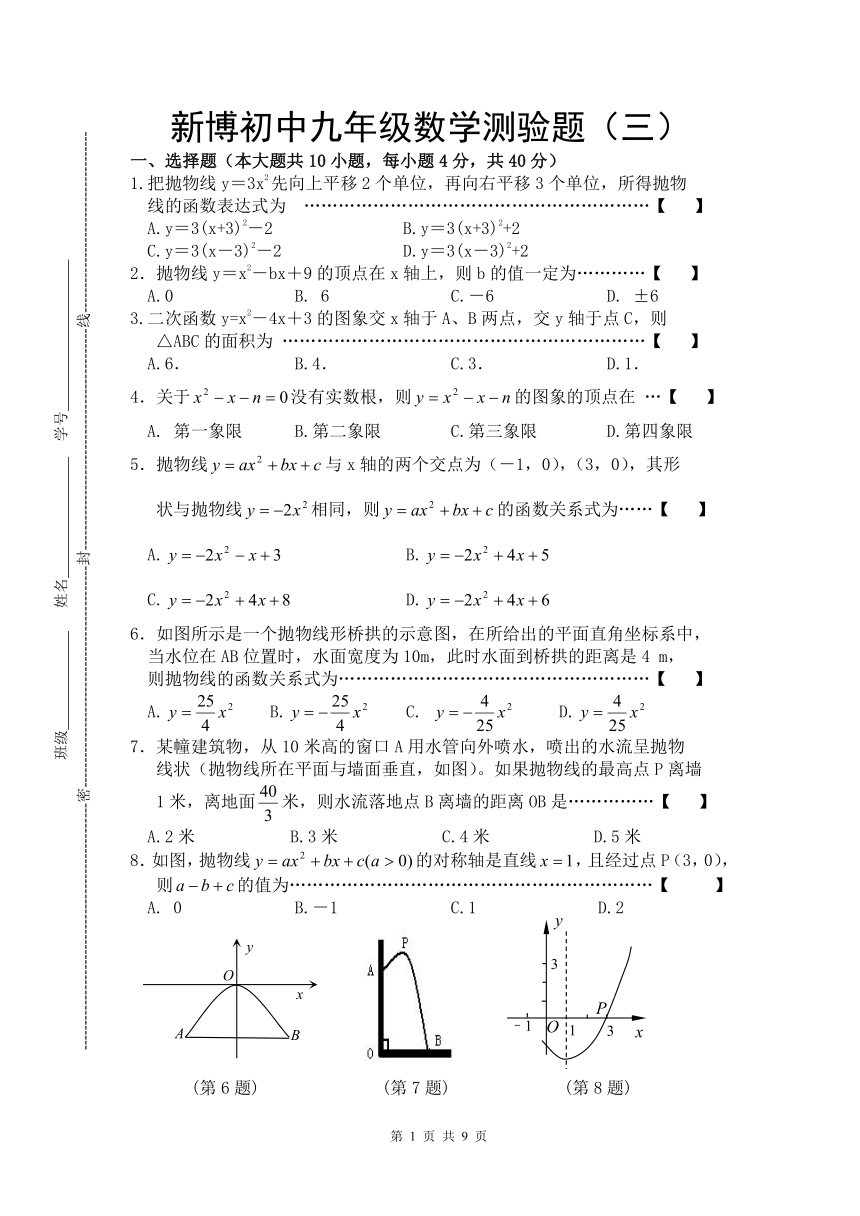 | |
| 格式 | rar | ||
| 文件大小 | 102.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-08 11:30:00 | ||
图片预览



文档简介
新博初中九年级数学测验题(三)
一、选择题(本大题共10小题,每小题4分,共40分)
1.把抛物线y=3x2先向上平移2个单位,再向右平移3个单位,所得抛物
线的函数表达式为 ……………………………………………………【 】
A.y=3(x+3)2-2 B.y=3(x+3)2+2
C.y=3(x-3)2-2 D.y=3(x-3)2+2
2.抛物线y=x2-bx+9的顶点在x轴上,则b的值一定为…………【 】
A.0 B. 6 C.-6 D. ±6
3.二次函数y=x2-4x+3的图象交x轴于A、B两点,交y轴于点C,则
△ABC的面积为 ………………………………………………………【 】
A.6. B.4. C.3. D.1.
4.关于没有实数根,则的图象的顶点在 …【 】
A. 第一象限 B.第二象限 C.第三象限 D.第四象限
5.抛物线与x轴的两个交点为(-1,0),(3,0),其形
状与抛物线相同,则的函数关系式为……【 】
A. B.
C. D.
6.如图所示是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,
当水位在AB位置时,水面宽度为10m,此时水面到桥拱的距离是4 m,
则抛物线的函数关系式为………………………………………………【 】
A. B. HYPERLINK "http://www./Index.html" C. D.
7.某幢建筑物,从10米高的窗口A用水管向外喷水,喷出的水流呈抛物
线状(抛物线所在平面与墙面垂直,如图)。如果抛物线的最高点P离墙
1米,离地面米,则水流落地点B离墙的距离OB是……………【 】
A.2米 B.3米 C.4米 D.5米
8.如图,抛物线的对称轴是直线,且经过点P(3,0),则的值为………………………………………………………【 】
A. 0 B.-1 C.1 D.2
(第6题) (第7题) (第8题)
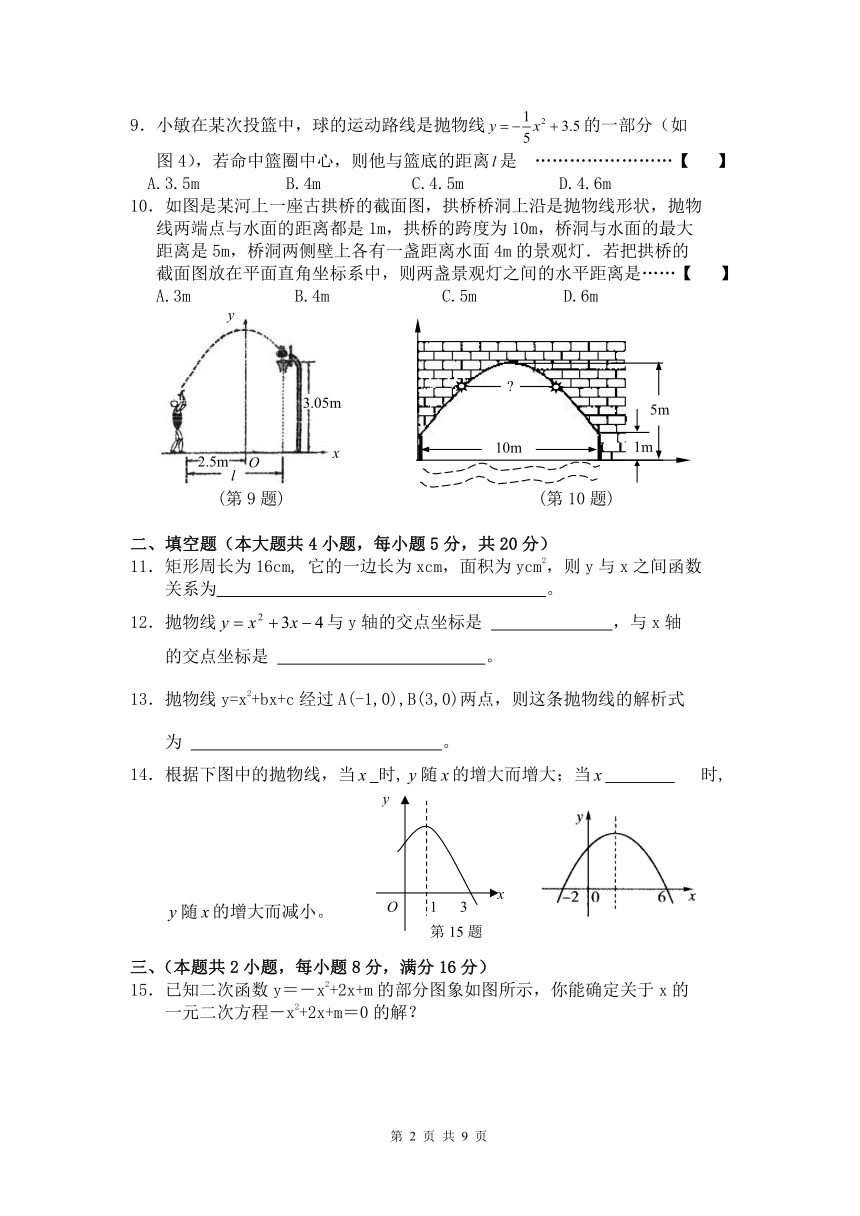
9.小敏在某次投篮中,球的运动路线是抛物线 HYPERLINK "http://www./Index.html" 的一部分(如
图4),若命中篮圈中心,则他与篮底的距离是 ……………………【 】
A.3.5m B.4m C.4.5m D.4.6m
10.如图是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物
线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大
距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.若把拱桥的
截面图放在平面直角坐标系中,则两盏景观灯之间的水平距离是……【 】
A.3m B.4m C.5m D.6m
(第9题) (第10题)
二、填空题(本大题共4小题,每小题5分,共20分)
11.矩形周长为16cm, 它的一边长为xcm,面积为ycm2,则y与x之间函数
关系为 。
12.抛物线与y轴的交点坐标是 ,与x轴
的交点坐标是 。
13.抛物线y=x2+bx+c经过A(-1,0),B(3,0)两点,则这条抛物线的解析式
为 。
根据下图中的抛物线,当 时,随的增大而增大;当 时,
随的增大而减小。
三、(本题共2小题,每小题8分,满分16分)
15.已知二次函数y=-x2+2x+m的部分图象如图所示,你能确定关于x的
一元二次方程-x2+2x+m=0的解?
16.竖直向上发射物体的高度h(m)满足关系式h=-5t2+v0·t,其中
t(s)是物体运动的时间,v0(m/s)是物体被发射时的速度。某公园
计划设计园内喷泉,喷水的最大高度要求达到15m,那么喷水的速度应
该达到多少?(结果精确到0.01m/s)
四、(本题共2小题,每小题8分,满分16分)
17.已知二次函数。
(1)求证:对于任意实数m,该二次函数图象与x轴总有公共点;
(2)若该二次函数图象与x轴有两个公共点A,B,且A点坐标为
(1,0),求B点坐标。
18.二次函数y=ax2+bx+c(a≠0,a,b,c是常数)中,自变量x与函数y
的对应值如下表:
x -1 - 0 1 2 3
y -2 - 1 2 1 - -2
(1)判断二次函数图象的开口方向,并写出它的顶点坐标。
(2)一元二次方程ax2+bx+c=0(a≠0,a,b,c是常数)的两个根x1,x2的取值范围是下列选项中的哪一个 。
①-<x1<0, HYPERLINK "http://www./Index.html" <x2<2 ;②-1<x1<-,2<x2<;③-<x1<0,2<x2<;④-1<x1<-,<x2<2。
五、(本题共2小题,每小题10分,满分20分)
19.某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克。经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克。
(1)现该商场要保证每天盈利6000元,同时又要顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
20.施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系(如图1所示)。
(1)直接写出点M及抛物线顶点P的坐标;
(2)求出这条抛物线的函数关系式;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”CDAB,使A、D点在抛物线上,B、C点在地面OM上.为了筹备材料,需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少?
六、(本大题满分12分)
21.二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
(1)写出方程ax2+bx+c=0的两个根。
(2)写出不等式ax2+bx+c>0的解集。
(3)写出y随x的增大而减小的自变量x的取值范围。
(4)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围。
七、(本大题满分12分)
22.一座隧道的截面由抛物线和长方形构成,长方形的长为,宽为,
隧道最高点P位于AB的中央且距地面,建立如图所示的坐标系:
(1)求抛物线的解析式;
(2)一辆货车高,宽,能否从该隧道内通过,为什么?
(3)如果隧道内设双行道,那么这辆货车是否可以顺利通过,为什么?
八、(本大题满分14分)
23.(1)把二次函数HYPERLINK "http://www./Index.html"化成y=a(x-h)2+k的形式.;
(2)写出抛物线的顶点坐标和对称轴,并说明该
抛物线是由哪一条形如y=ax2的抛物线经过怎样的变换得到的?
(3)如果抛物线 HYPERLINK "http://www./Index.html" 中,x的取值范围是0≤x≤3,请
画出图象,并试着给该抛物线编一个具有实际意义的情境(如喷水、
掷物、投篮等)。
答案
一、选择题(本大题共10小题,每小题4分,共40分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D D C A D C B A B C
二、填空题(本大题共4小题,每小题5分,共20分)
11. y=-x2+8x 12.(0,-4);(1,0),(-4,0)
13. y=x2-2x-3 14.<2;>2
三、(本题共2小题,每小题8分,满分16分)
15.解 因为抛物线的对称轴x1=1,与x轴的一个交点坐标是(3,0),
所以抛物线与x轴的一个交点坐标是(-1,0),
所以关于x的一元二次方程-x2+2x+m=0的解为x1=-1,x2=3.
说明 设二次函数y=ax2+bx+c的图象上两点(x1,y),(x2,y),则抛
物线的对称轴方程是x= HYPERLINK "http://www./Index.html" 。
16.解:y=-5t2+v0·t,其对称轴为t=- HYPERLINK "http://www./Index.html" 。
∴当t=时,ymax=-5·()2+v0·==15,v=300,
∴v0=10=17.32(m/s)。
答:喷水的速度应该达到17.23m/s。
四、(本题共2小题,每小题8分,满分16分)
17.(1),
∵,∴。
∴对于任意实数,该二次函数图象与轴总有公共点。
(2)把(1,0)代入二次函数关系式,得,
∴,,
,B(-2,0),,(,0)。
18.观察表中的数据特征,对应的点坐标是关于x=1对称,且开口向下,
并且顶点坐标(1,2),从而可以进一步求解。
(1)因为对应的点坐标都是关于直线x=1对称,并由点坐标的特征可
知二次函数图象的开口向下,且顶点坐标(1,2)。
(2)由此-<x1<0,2<x2< HYPERLINK "http://www./Index.html" .所以两个根x1,x2的取值范围是③。
五、(本题共2小题,每小题10分,满分20分)
19.(1)设每千克应涨价x元,则(10+x)(500-20x)=6000
解得x=5或x=10,
为了使顾客得到实惠,所以x=5。
(2)设涨价x元时总利润为y,则
y=(10+x)(500-20x)= -20x2+300x+5000=-20(x-7.5) 2+6125
当x=7.5时,y取得最大值,最大值为6125。
答:(1)要保证每天盈利6000元,同时又使顾客得到实惠,那么每千克
应涨价5元;(2)若该商场单纯从经济角度看,每千克这种水
果涨价7.5元,能使商场获利最多。
20.解:(1)M(12,0),P(6,6).
(2)设这条抛物线的函数关系式为:y=a(x-6)2+6 , ·
∵抛物线过0(0,0),∴a(0-6)2+6=0,解得,
∴这条抛物线的函数关系式为:y=-(x-6)2+6,即.
(3)设OB=m,米,则点A的坐标为(m, -m2+2m),
∴AB=DC=.
根据抛物线的轴对称,可得:OB=CM=m,所以BC=12-2m, 即AD=12-2m,
∴=AB+AD+DC=
==,
∴当m=3,即OB=3米时,三根木杆长度之和l的最大值为15米。
六、(本大题满分12分)
21.(1)由题意可知抛物线的顶点坐标(4,6),
设抛物线的方程为,
又因为点A(0,2)在抛物线上,
所以有 HYPERLINK "http://www./Index.html" .所以a=。
因此有: HYPERLINK "http://www./Index.html" 。
(2)令,则有 。
解得 HYPERLINK "http://www./Index.html" 。
。
∴货车可以通过。
(3)由(2)可知 HYPERLINK "http://www./Index.html" ,
∴货车可以通过。
七、(本大题满分12分)
22.解(1)因为二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点坐标
是(1,0)(3,0),所以方程ax2+bx+c=0的两个根为x1=1,x2=3。
(2)因为抛物线的开口向下,所以x轴的上方都满足ax2+bx+c>0,即
不等式ax2+bx+c>0的解集为1<x<3。
(3)因为抛物线的对称轴方程是x=2,且a<0,所以当x>2时,y
随x的增大而减小。
(4)因为抛物线的顶点的纵坐标是2,所以要使方程ax2+bx+c=k有两
个不相等的实数根,只要k<2。
(本大题满分14分)
23.解:(1) HYPERLINK "http://www./Index.html" EMBED Equation.DSMT4
HYPERLINK "http://" EMBED Equation.DSMT4 。
(2)由上式可知抛物线的顶点坐标为,其对称轴为直线x=1,该
抛物线是由抛物线向右平移1个单位,再向上平移3个单位
(或向上平移3个单位,再向右平移1个单位)得到的.(3)抛物线与
轴交于,与轴交于 HYPERLINK "http://www./Index.html" ,顶点为,把这三个点用平滑
的曲线连接起来就得到抛物线在的图象(如图所示)。情境示例不惟一,如:小明在平台上,从离地面2.25米处抛出一物体,落在离平台底部水平距离为3米的地面上,物体离地面的最大高度为3米。
班级 姓名 学号
-------------------------------------------------密--------------------------------------------封--------------------------------------------线------------------------------------
–1
3
3
1
x
B
y
O
A
5m
1m
10m
2.5m
3.05m
y
x
O
1
3
第15题
x
y
3
3
2
2
1
1
4
-1
-1
-2
O
y
x
3
1
0
(1,3)
第 1 页 共 5 页
一、选择题(本大题共10小题,每小题4分,共40分)
1.把抛物线y=3x2先向上平移2个单位,再向右平移3个单位,所得抛物
线的函数表达式为 ……………………………………………………【 】
A.y=3(x+3)2-2 B.y=3(x+3)2+2
C.y=3(x-3)2-2 D.y=3(x-3)2+2
2.抛物线y=x2-bx+9的顶点在x轴上,则b的值一定为…………【 】
A.0 B. 6 C.-6 D. ±6
3.二次函数y=x2-4x+3的图象交x轴于A、B两点,交y轴于点C,则
△ABC的面积为 ………………………………………………………【 】
A.6. B.4. C.3. D.1.
4.关于没有实数根,则的图象的顶点在 …【 】
A. 第一象限 B.第二象限 C.第三象限 D.第四象限
5.抛物线与x轴的两个交点为(-1,0),(3,0),其形
状与抛物线相同,则的函数关系式为……【 】
A. B.
C. D.
6.如图所示是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,
当水位在AB位置时,水面宽度为10m,此时水面到桥拱的距离是4 m,
则抛物线的函数关系式为………………………………………………【 】
A. B. HYPERLINK "http://www./Index.html" C. D.
7.某幢建筑物,从10米高的窗口A用水管向外喷水,喷出的水流呈抛物
线状(抛物线所在平面与墙面垂直,如图)。如果抛物线的最高点P离墙
1米,离地面米,则水流落地点B离墙的距离OB是……………【 】
A.2米 B.3米 C.4米 D.5米
8.如图,抛物线的对称轴是直线,且经过点P(3,0),则的值为………………………………………………………【 】
A. 0 B.-1 C.1 D.2
(第6题) (第7题) (第8题)
9.小敏在某次投篮中,球的运动路线是抛物线 HYPERLINK "http://www./Index.html" 的一部分(如
图4),若命中篮圈中心,则他与篮底的距离是 ……………………【 】
A.3.5m B.4m C.4.5m D.4.6m
10.如图是某河上一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物
线两端点与水面的距离都是1m,拱桥的跨度为10m,桥洞与水面的最大
距离是5m,桥洞两侧壁上各有一盏距离水面4m的景观灯.若把拱桥的
截面图放在平面直角坐标系中,则两盏景观灯之间的水平距离是……【 】
A.3m B.4m C.5m D.6m
(第9题) (第10题)
二、填空题(本大题共4小题,每小题5分,共20分)
11.矩形周长为16cm, 它的一边长为xcm,面积为ycm2,则y与x之间函数
关系为 。
12.抛物线与y轴的交点坐标是 ,与x轴
的交点坐标是 。
13.抛物线y=x2+bx+c经过A(-1,0),B(3,0)两点,则这条抛物线的解析式
为 。
根据下图中的抛物线,当 时,随的增大而增大;当 时,
随的增大而减小。
三、(本题共2小题,每小题8分,满分16分)
15.已知二次函数y=-x2+2x+m的部分图象如图所示,你能确定关于x的
一元二次方程-x2+2x+m=0的解?
16.竖直向上发射物体的高度h(m)满足关系式h=-5t2+v0·t,其中
t(s)是物体运动的时间,v0(m/s)是物体被发射时的速度。某公园
计划设计园内喷泉,喷水的最大高度要求达到15m,那么喷水的速度应
该达到多少?(结果精确到0.01m/s)
四、(本题共2小题,每小题8分,满分16分)
17.已知二次函数。
(1)求证:对于任意实数m,该二次函数图象与x轴总有公共点;
(2)若该二次函数图象与x轴有两个公共点A,B,且A点坐标为
(1,0),求B点坐标。
18.二次函数y=ax2+bx+c(a≠0,a,b,c是常数)中,自变量x与函数y
的对应值如下表:
x -1 - 0 1 2 3
y -2 - 1 2 1 - -2
(1)判断二次函数图象的开口方向,并写出它的顶点坐标。
(2)一元二次方程ax2+bx+c=0(a≠0,a,b,c是常数)的两个根x1,x2的取值范围是下列选项中的哪一个 。
①-<x1<0, HYPERLINK "http://www./Index.html" <x2<2 ;②-1<x1<-,2<x2<;③-<x1<0,2<x2<;④-1<x1<-,<x2<2。
五、(本题共2小题,每小题10分,满分20分)
19.某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克。经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克。
(1)现该商场要保证每天盈利6000元,同时又要顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
20.施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系(如图1所示)。
(1)直接写出点M及抛物线顶点P的坐标;
(2)求出这条抛物线的函数关系式;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”CDAB,使A、D点在抛物线上,B、C点在地面OM上.为了筹备材料,需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少?
六、(本大题满分12分)
21.二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
(1)写出方程ax2+bx+c=0的两个根。
(2)写出不等式ax2+bx+c>0的解集。
(3)写出y随x的增大而减小的自变量x的取值范围。
(4)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围。
七、(本大题满分12分)
22.一座隧道的截面由抛物线和长方形构成,长方形的长为,宽为,
隧道最高点P位于AB的中央且距地面,建立如图所示的坐标系:
(1)求抛物线的解析式;
(2)一辆货车高,宽,能否从该隧道内通过,为什么?
(3)如果隧道内设双行道,那么这辆货车是否可以顺利通过,为什么?
八、(本大题满分14分)
23.(1)把二次函数HYPERLINK "http://www./Index.html"化成y=a(x-h)2+k的形式.;
(2)写出抛物线的顶点坐标和对称轴,并说明该
抛物线是由哪一条形如y=ax2的抛物线经过怎样的变换得到的?
(3)如果抛物线 HYPERLINK "http://www./Index.html" 中,x的取值范围是0≤x≤3,请
画出图象,并试着给该抛物线编一个具有实际意义的情境(如喷水、
掷物、投篮等)。
答案
一、选择题(本大题共10小题,每小题4分,共40分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D D C A D C B A B C
二、填空题(本大题共4小题,每小题5分,共20分)
11. y=-x2+8x 12.(0,-4);(1,0),(-4,0)
13. y=x2-2x-3 14.<2;>2
三、(本题共2小题,每小题8分,满分16分)
15.解 因为抛物线的对称轴x1=1,与x轴的一个交点坐标是(3,0),
所以抛物线与x轴的一个交点坐标是(-1,0),
所以关于x的一元二次方程-x2+2x+m=0的解为x1=-1,x2=3.
说明 设二次函数y=ax2+bx+c的图象上两点(x1,y),(x2,y),则抛
物线的对称轴方程是x= HYPERLINK "http://www./Index.html" 。
16.解:y=-5t2+v0·t,其对称轴为t=- HYPERLINK "http://www./Index.html" 。
∴当t=时,ymax=-5·()2+v0·==15,v=300,
∴v0=10=17.32(m/s)。
答:喷水的速度应该达到17.23m/s。
四、(本题共2小题,每小题8分,满分16分)
17.(1),
∵,∴。
∴对于任意实数,该二次函数图象与轴总有公共点。
(2)把(1,0)代入二次函数关系式,得,
∴,,
,B(-2,0),,(,0)。
18.观察表中的数据特征,对应的点坐标是关于x=1对称,且开口向下,
并且顶点坐标(1,2),从而可以进一步求解。
(1)因为对应的点坐标都是关于直线x=1对称,并由点坐标的特征可
知二次函数图象的开口向下,且顶点坐标(1,2)。
(2)由此-<x1<0,2<x2< HYPERLINK "http://www./Index.html" .所以两个根x1,x2的取值范围是③。
五、(本题共2小题,每小题10分,满分20分)
19.(1)设每千克应涨价x元,则(10+x)(500-20x)=6000
解得x=5或x=10,
为了使顾客得到实惠,所以x=5。
(2)设涨价x元时总利润为y,则
y=(10+x)(500-20x)= -20x2+300x+5000=-20(x-7.5) 2+6125
当x=7.5时,y取得最大值,最大值为6125。
答:(1)要保证每天盈利6000元,同时又使顾客得到实惠,那么每千克
应涨价5元;(2)若该商场单纯从经济角度看,每千克这种水
果涨价7.5元,能使商场获利最多。
20.解:(1)M(12,0),P(6,6).
(2)设这条抛物线的函数关系式为:y=a(x-6)2+6 , ·
∵抛物线过0(0,0),∴a(0-6)2+6=0,解得,
∴这条抛物线的函数关系式为:y=-(x-6)2+6,即.
(3)设OB=m,米,则点A的坐标为(m, -m2+2m),
∴AB=DC=.
根据抛物线的轴对称,可得:OB=CM=m,所以BC=12-2m, 即AD=12-2m,
∴=AB+AD+DC=
==,
∴当m=3,即OB=3米时,三根木杆长度之和l的最大值为15米。
六、(本大题满分12分)
21.(1)由题意可知抛物线的顶点坐标(4,6),
设抛物线的方程为,
又因为点A(0,2)在抛物线上,
所以有 HYPERLINK "http://www./Index.html" .所以a=。
因此有: HYPERLINK "http://www./Index.html" 。
(2)令,则有 。
解得 HYPERLINK "http://www./Index.html" 。
。
∴货车可以通过。
(3)由(2)可知 HYPERLINK "http://www./Index.html" ,
∴货车可以通过。
七、(本大题满分12分)
22.解(1)因为二次函数y=ax2+bx+c(a≠0)的图象与x轴的两个交点坐标
是(1,0)(3,0),所以方程ax2+bx+c=0的两个根为x1=1,x2=3。
(2)因为抛物线的开口向下,所以x轴的上方都满足ax2+bx+c>0,即
不等式ax2+bx+c>0的解集为1<x<3。
(3)因为抛物线的对称轴方程是x=2,且a<0,所以当x>2时,y
随x的增大而减小。
(4)因为抛物线的顶点的纵坐标是2,所以要使方程ax2+bx+c=k有两
个不相等的实数根,只要k<2。
(本大题满分14分)
23.解:(1) HYPERLINK "http://www./Index.html" EMBED Equation.DSMT4
HYPERLINK "http://" EMBED Equation.DSMT4 。
(2)由上式可知抛物线的顶点坐标为,其对称轴为直线x=1,该
抛物线是由抛物线向右平移1个单位,再向上平移3个单位
(或向上平移3个单位,再向右平移1个单位)得到的.(3)抛物线与
轴交于,与轴交于 HYPERLINK "http://www./Index.html" ,顶点为,把这三个点用平滑
的曲线连接起来就得到抛物线在的图象(如图所示)。情境示例不惟一,如:小明在平台上,从离地面2.25米处抛出一物体,落在离平台底部水平距离为3米的地面上,物体离地面的最大高度为3米。
班级 姓名 学号
-------------------------------------------------密--------------------------------------------封--------------------------------------------线------------------------------------
–1
3
3
1
x
B
y
O
A
5m
1m
10m
2.5m
3.05m
y
x
O
1
3
第15题
x
y
3
3
2
2
1
1
4
-1
-1
-2
O
y
x
3
1
0
(1,3)
第 1 页 共 5 页
