《平行四边形及其性质》学案
文档属性
| 名称 | 《平行四边形及其性质》学案 |

|
|
| 格式 | rar | ||
| 文件大小 | 51.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-06 00:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
《平行四边形及其性质》学案
19.1.1 平行四边形及其性质(一)
学习目标:
1、理解并掌握平行四边形的概念和平行四边形对边、对角相等的性质.
2、会用平行四边形的性质解决简单的平行四边形的计算问题,并会进行有关的论证.
3、培养学生发现问题、解决问题的能力及逻辑推理能力.
重、难点
1、重点:平行四边形的定义,平行四边形对角、对边相等的性质,以及性质的应用.
2、难点:运用平行四边形的性质进行有关的论证和计算.
学习过程
一、学前准备
1、平行四边形是我们常见的图形,你还能举出平行四边形在生活中应用的例子吗?
你能总结出平行四边形的定义吗?
2、在四边形ABCD中,AB∥DC,AD∥BC,那么四边形ABCD是平行四边形.平行四边形ABCD记作“ ABCD”,读作“平行四边形ABCD”.
①∵AB//DC ,AD//BC ,
∴四边形ABCD是平行四边形(判定);
②∵四边形ABCD是平行四边形∴AB//DC, AD//BC(性质).
3、证明平行四边形的对边相等、对角相等.
4、如图,在ABCD中,AE=CF,求证:AF=CE.
二、随堂练习
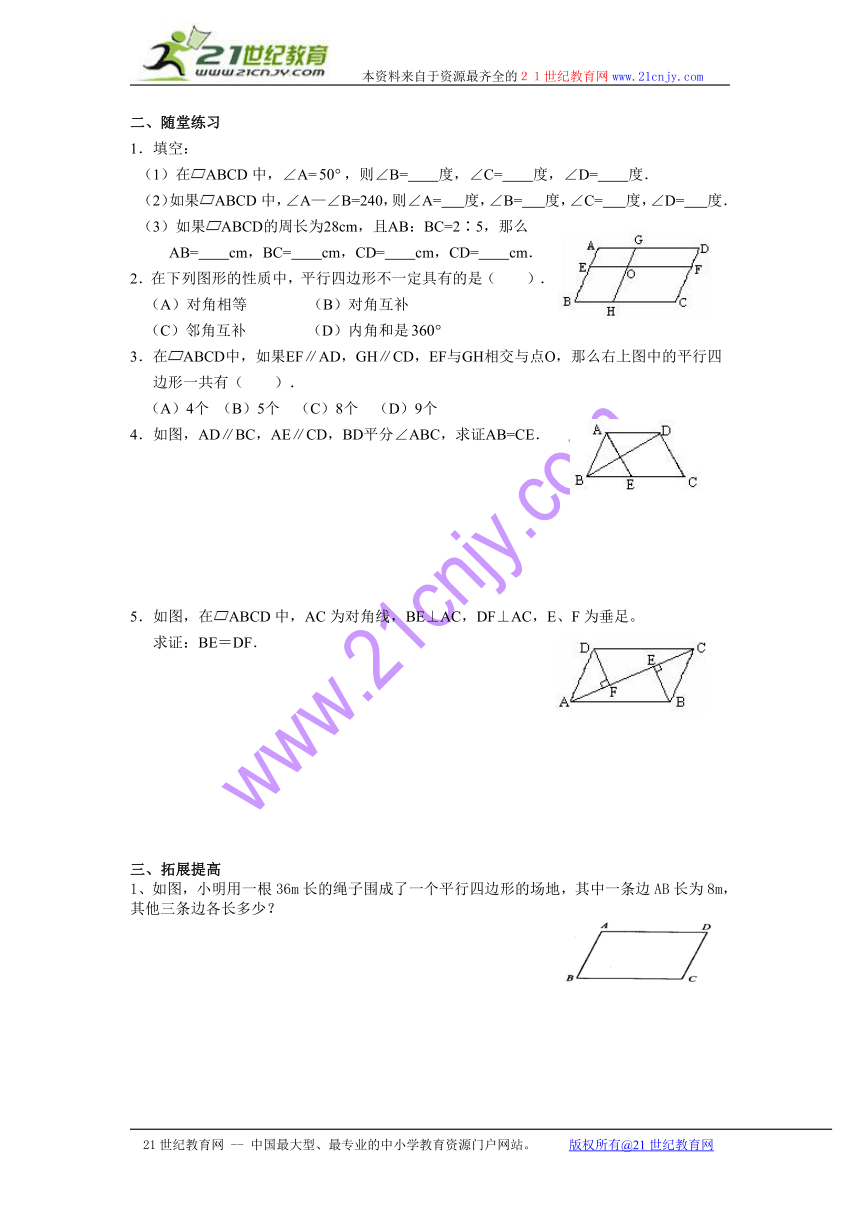
1.填空:
(1)在ABCD中,∠A=,则∠B= 度,∠C= 度,∠D= 度.
(2)如果ABCD中,∠A—∠B=240,则∠A= 度,∠B= 度,∠C= 度,∠D= 度.
(3)如果ABCD的周长为28cm,且AB:BC=2∶5,那么 AB= cm,BC= cm,CD= cm,CD= cm.
2.在下列图形的性质中,平行四边形不一定具有的是( ).
(A)对角相等 (B)对角互补
(C)邻角互补 (D)内角和是
3.在ABCD中,如果EF∥AD,GH∥CD,EF与GH相交与点O,那么右上图中的平行四边形一共有( ).
(A)4个 (B)5个 (C)8个 (D)9个
4.如图,AD∥BC,AE∥CD,BD平分∠ABC,求证AB=CE.
5.如图,在ABCD中,AC为对角线,BE⊥AC,DF⊥AC,E、F为垂足。
求证:BE=DF.
三、拓展提高
1、如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
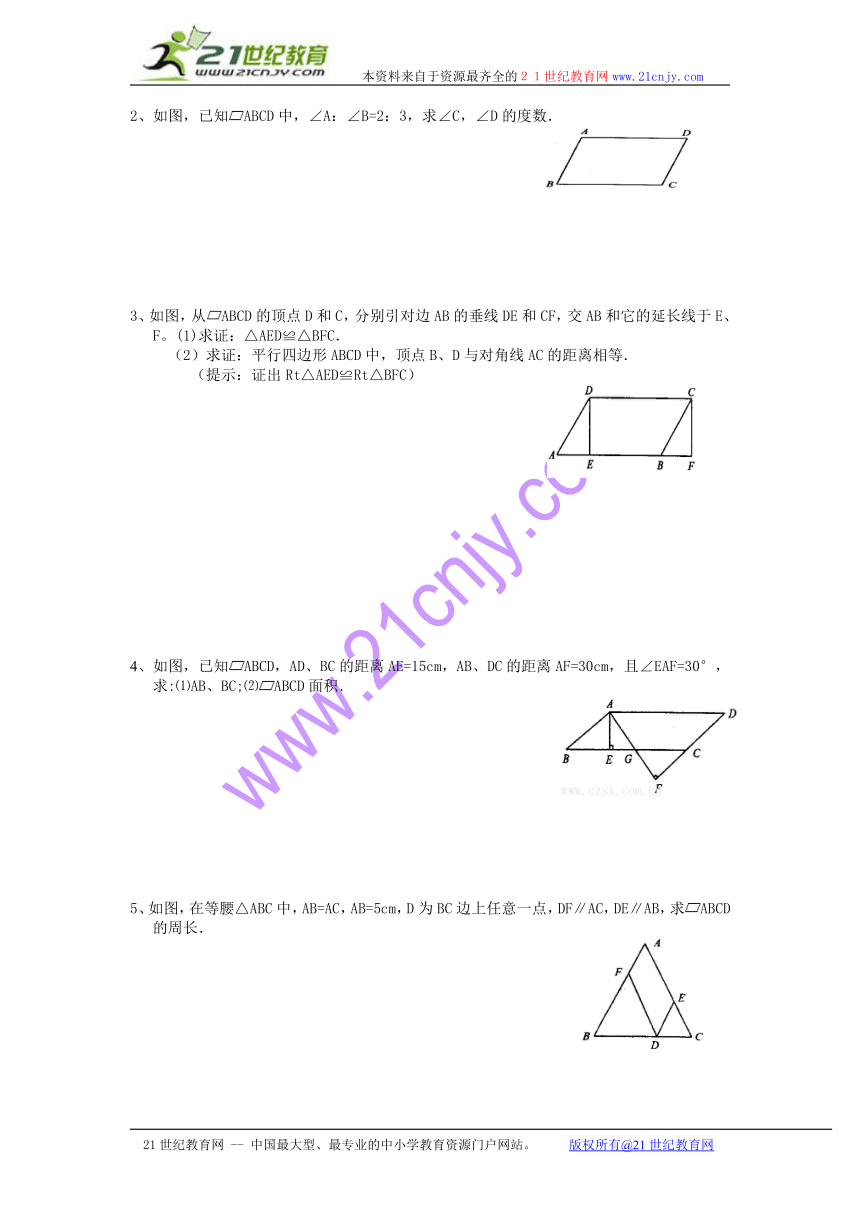
2、如图,已知ABCD中,∠A:∠B=2:3,求∠C,∠D的度数.
3、如图,从ABCD的顶点D和C,分别引对边AB的垂线DE和CF,交AB和它的延长线于E、F。(1)求证:△AED≌△BFC.
(2)求证:平行四边形ABCD中,顶点B、D与对角线AC的距离相等.
(提示:证出Rt△AED≌Rt△BFC)
4、如图,已知ABCD,AD、BC的距离AE=15cm,AB、DC的距离AF=30cm,且∠EAF=30°,求:⑴AB、BC;⑵ABCD面积.
5、如图,在等腰△ABC中,AB=AC,AB=5cm,D为BC边上任意一点,DF∥AC,DE∥AB,求ABCD的周长.
6、如图所示,在ABCD中,点E、F在对角线AC上,且AE=CF,请你以F为一个端点,和图中已标明字母的某一点连成一条新线段,猜想并证明它和图中已有的一条线段相等(只须证明一组线段相等即可).
(1)连结:__________.
(2)猜想:________=________.
(3)证明.
四、尝试小结
19.1.1平行四边形及其性质(二)
自学目标:
1、理解平行四边形中心对称的特征,掌握平行四边形对角线互相平分的性质.
2、能综合运用平行四边形的性质解决平行四边形的有关计算问题,和简单的证明题.
3、培养学生的推理论证能力和逻辑思维能力.
重、难点:
1、重点:平行四边形对角线互相平分的性质,以及性质的应用.
2、难点:综合运用平行四边形的性质进行有关的论证和计算.
自学过程:
1、 课前准备
1 什么样的四边形是平行四边形?平行四边形的性质?
2 如图,ABCD中,AE⊥BD,∠EAD=60°,AE=2cm,AC+BD=14cm,则△OBC的周长是____ ___cm.
3 ABCD一内角的平分线与边相交并把这条边分成,的两条线段,
则ABCD的周长是__ ___.
5 在平行四边形中,周长等于48,⑴已知一边长12,求各边的长。⑵已知AB=2BC,求各边的长。⑶已知对角线AC、BD交于点O,△AOD与△AOB的周长的差是10,求各边的长。
二、课堂练习
1、在 ABCD中,AC=6、BD=4,则AB的范围是__ ______.
2、在平行四边形ABCD中,已知AB、BC、CD三条边的长度分别为(x+3),(x-4)和16,则这个四边形的周长是 .
3、公园有一片绿地,它的形状是平行四边形,绿地上要修几条笔直的小路,如图,AB=15cm,AD=12cm,AC⊥BC,求小路BC,CD,OC的长,并算出绿地的面积.
4、已知如右图,在ABCD中,AB=10cm,AD=8cm,AC⊥BC,求BC、CD、AC、OA的长以及ABCD的面积.
5、已知:如图4-21, ABCD的对角线AC、BD相交于点O,EF过点O与AB、CD分别相交于点E、F.
求证:OE=OF,AE=CF,BE=DF.
6、如图,在平行四边形ABCD中,BC=2AB,E为BC的中点,求∠AED的度数.
三、拓展提高
1、如图,在□ABCD中,O是对角线AC、BD的交点,BE⊥AC,DF⊥AC,垂足分别为E、F.那么OE与OF是否相等?为什么?
2、如图,□ABCD中,∠ABC=3∠A,F是CB的延长线上一点,EF⊥DC于E,CF=CD,若EF=3cm,求DE长.
3、如图,□ABCD中,AE⊥BC,AF⊥CD,∠EAF=30°,AE=4cm,AF=3cm,求□ABCD周长.
4、如图,E、F是□ABCD的对角线AC上的两点,AE=CF.
求证:(1)△ABE≌△CDF;
(2)BE∥DF.
5、如图,已知□ABCD的对角线AC、BD相交于点O,EF过点O,且与BC、AD分别相交于点E、F,求证:OE=OF.
四、尝试小结
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
《平行四边形及其性质》学案
19.1.1 平行四边形及其性质(一)
学习目标:
1、理解并掌握平行四边形的概念和平行四边形对边、对角相等的性质.
2、会用平行四边形的性质解决简单的平行四边形的计算问题,并会进行有关的论证.
3、培养学生发现问题、解决问题的能力及逻辑推理能力.
重、难点
1、重点:平行四边形的定义,平行四边形对角、对边相等的性质,以及性质的应用.
2、难点:运用平行四边形的性质进行有关的论证和计算.
学习过程
一、学前准备
1、平行四边形是我们常见的图形,你还能举出平行四边形在生活中应用的例子吗?
你能总结出平行四边形的定义吗?
2、在四边形ABCD中,AB∥DC,AD∥BC,那么四边形ABCD是平行四边形.平行四边形ABCD记作“ ABCD”,读作“平行四边形ABCD”.
①∵AB//DC ,AD//BC ,
∴四边形ABCD是平行四边形(判定);
②∵四边形ABCD是平行四边形∴AB//DC, AD//BC(性质).
3、证明平行四边形的对边相等、对角相等.
4、如图,在ABCD中,AE=CF,求证:AF=CE.
二、随堂练习
1.填空:
(1)在ABCD中,∠A=,则∠B= 度,∠C= 度,∠D= 度.
(2)如果ABCD中,∠A—∠B=240,则∠A= 度,∠B= 度,∠C= 度,∠D= 度.
(3)如果ABCD的周长为28cm,且AB:BC=2∶5,那么 AB= cm,BC= cm,CD= cm,CD= cm.
2.在下列图形的性质中,平行四边形不一定具有的是( ).
(A)对角相等 (B)对角互补
(C)邻角互补 (D)内角和是
3.在ABCD中,如果EF∥AD,GH∥CD,EF与GH相交与点O,那么右上图中的平行四边形一共有( ).
(A)4个 (B)5个 (C)8个 (D)9个
4.如图,AD∥BC,AE∥CD,BD平分∠ABC,求证AB=CE.
5.如图,在ABCD中,AC为对角线,BE⊥AC,DF⊥AC,E、F为垂足。
求证:BE=DF.
三、拓展提高
1、如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?
2、如图,已知ABCD中,∠A:∠B=2:3,求∠C,∠D的度数.
3、如图,从ABCD的顶点D和C,分别引对边AB的垂线DE和CF,交AB和它的延长线于E、F。(1)求证:△AED≌△BFC.
(2)求证:平行四边形ABCD中,顶点B、D与对角线AC的距离相等.
(提示:证出Rt△AED≌Rt△BFC)
4、如图,已知ABCD,AD、BC的距离AE=15cm,AB、DC的距离AF=30cm,且∠EAF=30°,求:⑴AB、BC;⑵ABCD面积.
5、如图,在等腰△ABC中,AB=AC,AB=5cm,D为BC边上任意一点,DF∥AC,DE∥AB,求ABCD的周长.
6、如图所示,在ABCD中,点E、F在对角线AC上,且AE=CF,请你以F为一个端点,和图中已标明字母的某一点连成一条新线段,猜想并证明它和图中已有的一条线段相等(只须证明一组线段相等即可).
(1)连结:__________.
(2)猜想:________=________.
(3)证明.
四、尝试小结
19.1.1平行四边形及其性质(二)
自学目标:
1、理解平行四边形中心对称的特征,掌握平行四边形对角线互相平分的性质.
2、能综合运用平行四边形的性质解决平行四边形的有关计算问题,和简单的证明题.
3、培养学生的推理论证能力和逻辑思维能力.
重、难点:
1、重点:平行四边形对角线互相平分的性质,以及性质的应用.
2、难点:综合运用平行四边形的性质进行有关的论证和计算.
自学过程:
1、 课前准备
1 什么样的四边形是平行四边形?平行四边形的性质?
2 如图,ABCD中,AE⊥BD,∠EAD=60°,AE=2cm,AC+BD=14cm,则△OBC的周长是____ ___cm.
3 ABCD一内角的平分线与边相交并把这条边分成,的两条线段,
则ABCD的周长是__ ___.
5 在平行四边形中,周长等于48,⑴已知一边长12,求各边的长。⑵已知AB=2BC,求各边的长。⑶已知对角线AC、BD交于点O,△AOD与△AOB的周长的差是10,求各边的长。
二、课堂练习
1、在 ABCD中,AC=6、BD=4,则AB的范围是__ ______.
2、在平行四边形ABCD中,已知AB、BC、CD三条边的长度分别为(x+3),(x-4)和16,则这个四边形的周长是 .
3、公园有一片绿地,它的形状是平行四边形,绿地上要修几条笔直的小路,如图,AB=15cm,AD=12cm,AC⊥BC,求小路BC,CD,OC的长,并算出绿地的面积.
4、已知如右图,在ABCD中,AB=10cm,AD=8cm,AC⊥BC,求BC、CD、AC、OA的长以及ABCD的面积.
5、已知:如图4-21, ABCD的对角线AC、BD相交于点O,EF过点O与AB、CD分别相交于点E、F.
求证:OE=OF,AE=CF,BE=DF.
6、如图,在平行四边形ABCD中,BC=2AB,E为BC的中点,求∠AED的度数.
三、拓展提高
1、如图,在□ABCD中,O是对角线AC、BD的交点,BE⊥AC,DF⊥AC,垂足分别为E、F.那么OE与OF是否相等?为什么?
2、如图,□ABCD中,∠ABC=3∠A,F是CB的延长线上一点,EF⊥DC于E,CF=CD,若EF=3cm,求DE长.
3、如图,□ABCD中,AE⊥BC,AF⊥CD,∠EAF=30°,AE=4cm,AF=3cm,求□ABCD周长.
4、如图,E、F是□ABCD的对角线AC上的两点,AE=CF.
求证:(1)△ABE≌△CDF;
(2)BE∥DF.
5、如图,已知□ABCD的对角线AC、BD相交于点O,EF过点O,且与BC、AD分别相交于点E、F,求证:OE=OF.
四、尝试小结
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
