《矩形》学案
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
《矩形》学案
19.2.1 特殊的平行四边形-矩形(一)
学习目标:
1.掌握矩形的概念和性质,理解矩形与平行四边形的区别与联系.
2.会初步运用矩形的概念和性质来解决有关问题.
3.渗透运动联系、从量变到质变的观点.
重点、难点
1.重点:矩形的性质.
2.难点:矩形的性质的灵活应用.
自学过程:
一、课前准备
1.展示生活中一些平行四边形的实际应用图片(推拉门,活动衣架,篱笆、井架等),想一想:这里面应用了平行四边形的什么性质?
2.思考:拿一个活动的平行四边形教具,轻轻拉动一个点,观察不管怎么拉,它还是一个平行四边形吗?为什么?
3.再次演示平行四边形的移动过程,当移动到一个角是直角时停止,让学生观察这是什么图形?
矩形定义:( )。
4.【探究】在一个平行四边形活动框架上,用两根橡皮筋分别套在相对的两个顶点上(作出对角线),拉动一对不相邻的顶点,改变平行四边形的形状.
① 随着∠α的变化,两条对角线的长度分别是怎样变化的?
② 当∠α是直角时,平行四边形变成矩形,此时它的其他内角是什么样的角?它的两条对角线的长度有什么关系?
操作,思考、交流、归纳后得到矩形的性质有哪些?
矩形性质1 ( ).
矩形性质2 ( )。
5.如图,在矩形ABCD中,AC、BD相交于点O,由性质2有AO=BO=CO=DO=AC=BD.因此可以得到直角三角形的一个性质:( )
二、课堂练习
1.(填空)
(1)矩形的定义中有两个条件:一是 ,二是 .
(2)已知矩形的一条对角线与一边的夹角为30°,则矩形两条对角线相交所得的四个角的度数分别为 、 、 、 .
(3)已知矩形的一条对角线长为10cm,两条对角线的一个交角为120°,则矩形的边长分别为 cm, cm, cm, cm.
2.(选择)
(1)下列说法错误的是( ).
(A)矩形的对角线互相平分 (B)矩形的对角线相等
(C)有一个角是直角的四边形是矩形 (D)有一个角是直角的平行四边形叫做矩形
(2)矩形的对角线把矩形分成的三角形中全等三角形一共有( ).
(A)2对 (B)4对 (C)6对 (D)8对
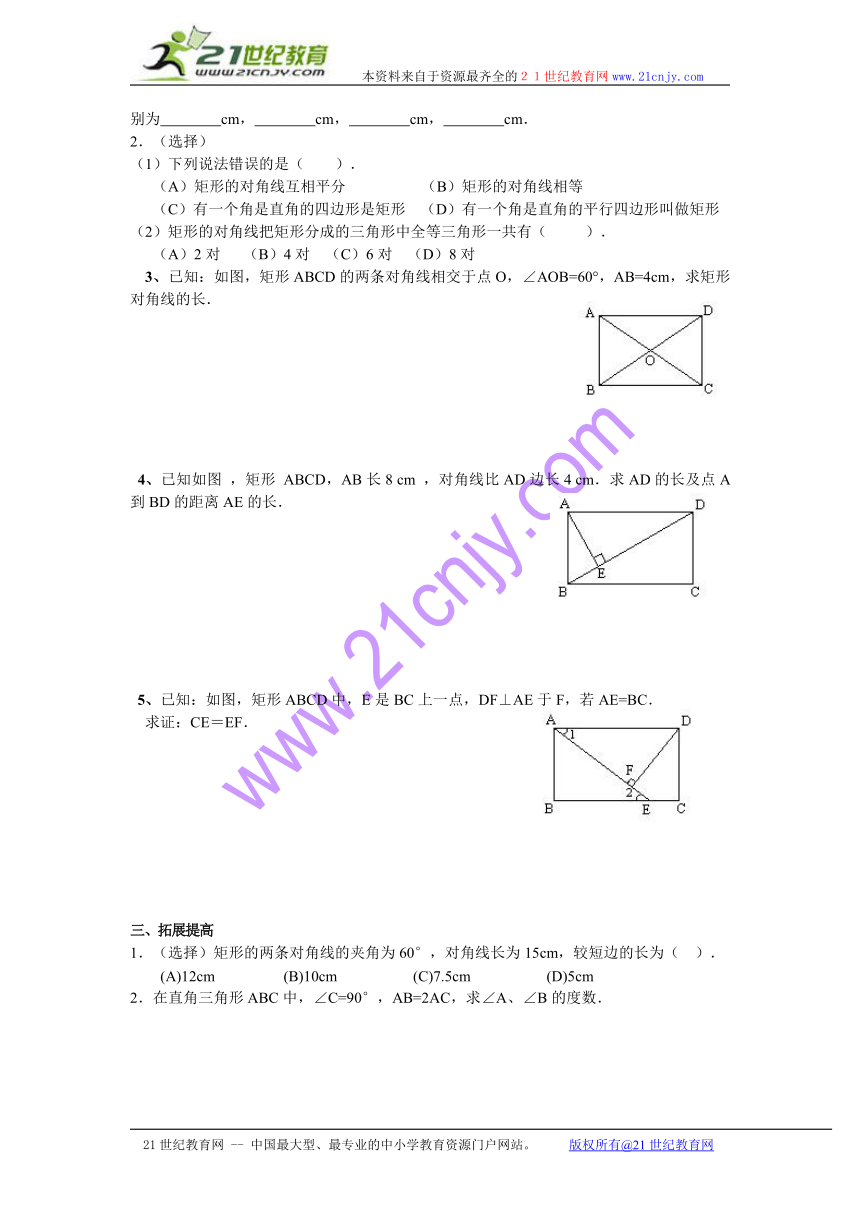
3、已知:如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4cm,求矩形对角线的长.
4、已知如图 ,矩形 ABCD,AB长8 cm ,对角线比AD边长4 cm.求AD的长及点A到BD的距离AE的长.
5、已知:如图,矩形ABCD中,E是BC上一点,DF⊥AE于F,若AE=BC.
求证:CE=EF.
三、拓展提高
1.(选择)矩形的两条对角线的夹角为60°,对角线长为15cm,较短边的长为( ).
(A)12cm (B)10cm (C)7.5cm (D)5cm
2.在直角三角形ABC中,∠C=90°,AB=2AC,求∠A、∠B的度数.
3.已知:矩形ABCD中,BC=2AB,E是BC的中点,求证:EA⊥ED.
4.如图,矩形ABCD中,AB=2BC,且AB=AE,求证:∠CBE的度数.
3.已知如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=120°,求∠AEO的度数.
四、尝试小结
19.2.1 特殊的平行四边形-矩形(二)
学习目标:
1.理解并掌握矩形的判定方法.
2.使学生能应用矩形定义、判定等知识,解决简单的证明题和计算题,进一步培养学生的分析能力
重、难点
1.重点:矩形的判定.
2.难点:矩形的判定及性质的综合应用.
自学过程:
一、课前准备
1.什么叫做平行四边形?什么叫做矩形?矩形有哪些性质?矩形与平行四边形有什么共同之处?有什么不同之处?
2.小华想要做一个矩形像框送给妈妈做生日礼物,于是找来两根长度相等的短木条和两根长度相等的长木条制作,你有什么办法可以检测他做的是矩形像框吗?看看谁的方法可行?
通过讨论得到矩形的判定方法.
矩形判定方法1:( ).
矩形判定方法2:( ).
3、已知 ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,AB=4 cm,求这个平行四边形的面积.
4、已知:如图(1),ABCD的四个内角的平分线分别相交于点E,F,G,H.求证:四边形EFGH是矩形.
二、课堂练习
1、下列各句判定矩形的说法是否正确?为什么?
(1)有一个角是直角的四边形是矩形; ( )
(2)有四个角是直角的四边形是矩形; ( )
(3)四个角都相等的四边形是矩形; ( )
(4)对角线相等的四边形是矩形; ( )
(5)对角线相等且互相垂直的四边形是矩形; ( )
(6)对角线互相平分且相等的四边形是矩形; ( )
(7)对角线相等,且有一个角是直角的四边形是矩形; ( )
(8)一组邻边垂直,一组对边平行且相等的四边形是矩形; ( )
(9)两组对边分别平行,且对角线相等的四边形是矩形. ( )
通过以上判断我们可以得出:
2、如图,AC,BD是矩形ABCD的两条对角线,AE=CG=BF=DH,求证:四边形EFGH是矩形.
3、如图,BD,BE分别是∠ABC与它的邻补角∠ABP的平分线,AE⊥BE,AD⊥BD,E,D为垂足.求证:四边形AEBD是矩形.
三、随堂练习
1.(选择)下列说法正确的是( ).
(A)有一组对角是直角的四边形一定是矩形
(B)有一组邻角是直角的四边形一定是矩形
(C)对角线互相平分的四边形是矩形
(D)对角互补的平行四边形是矩形
2.已知:如图 ,在△ABC中,∠C=90°, CD为中线,延长CD到点E,使得 DE=CD.连结AE,BE,则四边形ACBE为矩形.
3、如图,已知在四边形ABCD中,AC⊥DB,交于O、E、F、G、H分别是四边的中点;
求证:四边形EFGH是矩形.
4、如图,已知AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE,
求证:四边形BCED是矩形.(用两种证法)
5、已知:如图,矩形ABCD中,AE=DE,BE的延长线与CD的延长线相交于点F.
求证:S矩形ABCD=S△BCF.
6.如图,在△ABC中,AB=AC,PE⊥AB,PF⊥AC,CD⊥AB,垂足分别为E、D、F.
求证:PE-PF=CD.
四、尝试小结
G
O
F
E
H
C
B
A
D
B
D
C
P
E
A
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
《矩形》学案
19.2.1 特殊的平行四边形-矩形(一)
学习目标:
1.掌握矩形的概念和性质,理解矩形与平行四边形的区别与联系.
2.会初步运用矩形的概念和性质来解决有关问题.
3.渗透运动联系、从量变到质变的观点.
重点、难点
1.重点:矩形的性质.
2.难点:矩形的性质的灵活应用.
自学过程:
一、课前准备
1.展示生活中一些平行四边形的实际应用图片(推拉门,活动衣架,篱笆、井架等),想一想:这里面应用了平行四边形的什么性质?
2.思考:拿一个活动的平行四边形教具,轻轻拉动一个点,观察不管怎么拉,它还是一个平行四边形吗?为什么?
3.再次演示平行四边形的移动过程,当移动到一个角是直角时停止,让学生观察这是什么图形?
矩形定义:( )。
4.【探究】在一个平行四边形活动框架上,用两根橡皮筋分别套在相对的两个顶点上(作出对角线),拉动一对不相邻的顶点,改变平行四边形的形状.
① 随着∠α的变化,两条对角线的长度分别是怎样变化的?
② 当∠α是直角时,平行四边形变成矩形,此时它的其他内角是什么样的角?它的两条对角线的长度有什么关系?
操作,思考、交流、归纳后得到矩形的性质有哪些?
矩形性质1 ( ).
矩形性质2 ( )。
5.如图,在矩形ABCD中,AC、BD相交于点O,由性质2有AO=BO=CO=DO=AC=BD.因此可以得到直角三角形的一个性质:( )
二、课堂练习
1.(填空)
(1)矩形的定义中有两个条件:一是 ,二是 .
(2)已知矩形的一条对角线与一边的夹角为30°,则矩形两条对角线相交所得的四个角的度数分别为 、 、 、 .
(3)已知矩形的一条对角线长为10cm,两条对角线的一个交角为120°,则矩形的边长分别为 cm, cm, cm, cm.
2.(选择)
(1)下列说法错误的是( ).
(A)矩形的对角线互相平分 (B)矩形的对角线相等
(C)有一个角是直角的四边形是矩形 (D)有一个角是直角的平行四边形叫做矩形
(2)矩形的对角线把矩形分成的三角形中全等三角形一共有( ).
(A)2对 (B)4对 (C)6对 (D)8对
3、已知:如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=4cm,求矩形对角线的长.
4、已知如图 ,矩形 ABCD,AB长8 cm ,对角线比AD边长4 cm.求AD的长及点A到BD的距离AE的长.
5、已知:如图,矩形ABCD中,E是BC上一点,DF⊥AE于F,若AE=BC.
求证:CE=EF.
三、拓展提高
1.(选择)矩形的两条对角线的夹角为60°,对角线长为15cm,较短边的长为( ).
(A)12cm (B)10cm (C)7.5cm (D)5cm
2.在直角三角形ABC中,∠C=90°,AB=2AC,求∠A、∠B的度数.
3.已知:矩形ABCD中,BC=2AB,E是BC的中点,求证:EA⊥ED.
4.如图,矩形ABCD中,AB=2BC,且AB=AE,求证:∠CBE的度数.
3.已知如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=120°,求∠AEO的度数.
四、尝试小结
19.2.1 特殊的平行四边形-矩形(二)
学习目标:
1.理解并掌握矩形的判定方法.
2.使学生能应用矩形定义、判定等知识,解决简单的证明题和计算题,进一步培养学生的分析能力
重、难点
1.重点:矩形的判定.
2.难点:矩形的判定及性质的综合应用.
自学过程:
一、课前准备
1.什么叫做平行四边形?什么叫做矩形?矩形有哪些性质?矩形与平行四边形有什么共同之处?有什么不同之处?
2.小华想要做一个矩形像框送给妈妈做生日礼物,于是找来两根长度相等的短木条和两根长度相等的长木条制作,你有什么办法可以检测他做的是矩形像框吗?看看谁的方法可行?
通过讨论得到矩形的判定方法.
矩形判定方法1:( ).
矩形判定方法2:( ).
3、已知 ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,AB=4 cm,求这个平行四边形的面积.
4、已知:如图(1),ABCD的四个内角的平分线分别相交于点E,F,G,H.求证:四边形EFGH是矩形.
二、课堂练习
1、下列各句判定矩形的说法是否正确?为什么?
(1)有一个角是直角的四边形是矩形; ( )
(2)有四个角是直角的四边形是矩形; ( )
(3)四个角都相等的四边形是矩形; ( )
(4)对角线相等的四边形是矩形; ( )
(5)对角线相等且互相垂直的四边形是矩形; ( )
(6)对角线互相平分且相等的四边形是矩形; ( )
(7)对角线相等,且有一个角是直角的四边形是矩形; ( )
(8)一组邻边垂直,一组对边平行且相等的四边形是矩形; ( )
(9)两组对边分别平行,且对角线相等的四边形是矩形. ( )
通过以上判断我们可以得出:
2、如图,AC,BD是矩形ABCD的两条对角线,AE=CG=BF=DH,求证:四边形EFGH是矩形.
3、如图,BD,BE分别是∠ABC与它的邻补角∠ABP的平分线,AE⊥BE,AD⊥BD,E,D为垂足.求证:四边形AEBD是矩形.
三、随堂练习
1.(选择)下列说法正确的是( ).
(A)有一组对角是直角的四边形一定是矩形
(B)有一组邻角是直角的四边形一定是矩形
(C)对角线互相平分的四边形是矩形
(D)对角互补的平行四边形是矩形
2.已知:如图 ,在△ABC中,∠C=90°, CD为中线,延长CD到点E,使得 DE=CD.连结AE,BE,则四边形ACBE为矩形.
3、如图,已知在四边形ABCD中,AC⊥DB,交于O、E、F、G、H分别是四边的中点;
求证:四边形EFGH是矩形.
4、如图,已知AB=AC,AD=AE,DE=BC,且∠BAD=∠CAE,
求证:四边形BCED是矩形.(用两种证法)
5、已知:如图,矩形ABCD中,AE=DE,BE的延长线与CD的延长线相交于点F.
求证:S矩形ABCD=S△BCF.
6.如图,在△ABC中,AB=AC,PE⊥AB,PF⊥AC,CD⊥AB,垂足分别为E、D、F.
求证:PE-PF=CD.
四、尝试小结
G
O
F
E
H
C
B
A
D
B
D
C
P
E
A
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
