相似形检测（无答案）

相似形检测
1、 填空（每题4分，共48分）
1、若3x=4y，则 ；若，则 。
2、若，则 。
3、两个相似三角形的相似比为3：5，则对应中线的比等于 ，面积比为 。
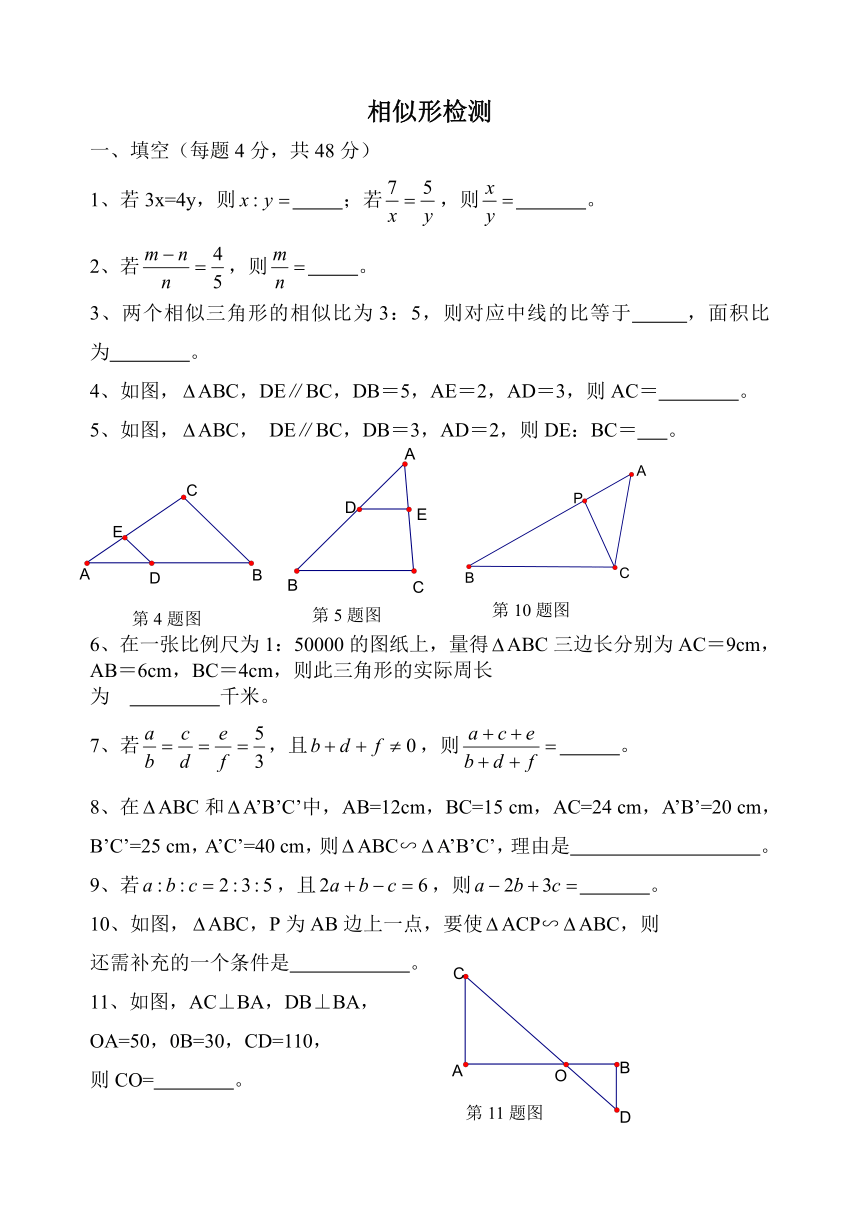
4、如图，ABC，DE∥BC，DB＝5，AE＝2，AD＝3，则AC＝ 。
5、如图，ABC， DE∥BC，DB＝3，AD＝2，则DE：BC＝ 。
6、在一张比例尺为1：50000的图纸上，量得ABC三边长分别为AC＝9cm，AB＝6cm，BC＝4cm，则此三角形的实际周长
为 千米。
7、若，且，则 。
8、在ABC和A’B’C’中，AB=12cm，BC=15 cm，AC=24 cm，A’B’=20 cm，B’C’=25 cm，A’C’=40 cm，则ABC∽A’B’C’，理由是 。
9、若，且，则 。
10、如图，ABC，P为AB边上一点，要使ACP∽ABC，则
还需补充的一个条件是 。
11、如图，AC⊥BA，DB⊥BA，
OA=50，0B=30，CD=110，
则CO= 。
12、P是RtABC的斜边BC上异于B、C的一点，过点P作直线截ABC，使截得的三角形与ABC相似，满足这样条件的直线共有 条。
2、 解答题（共24分）
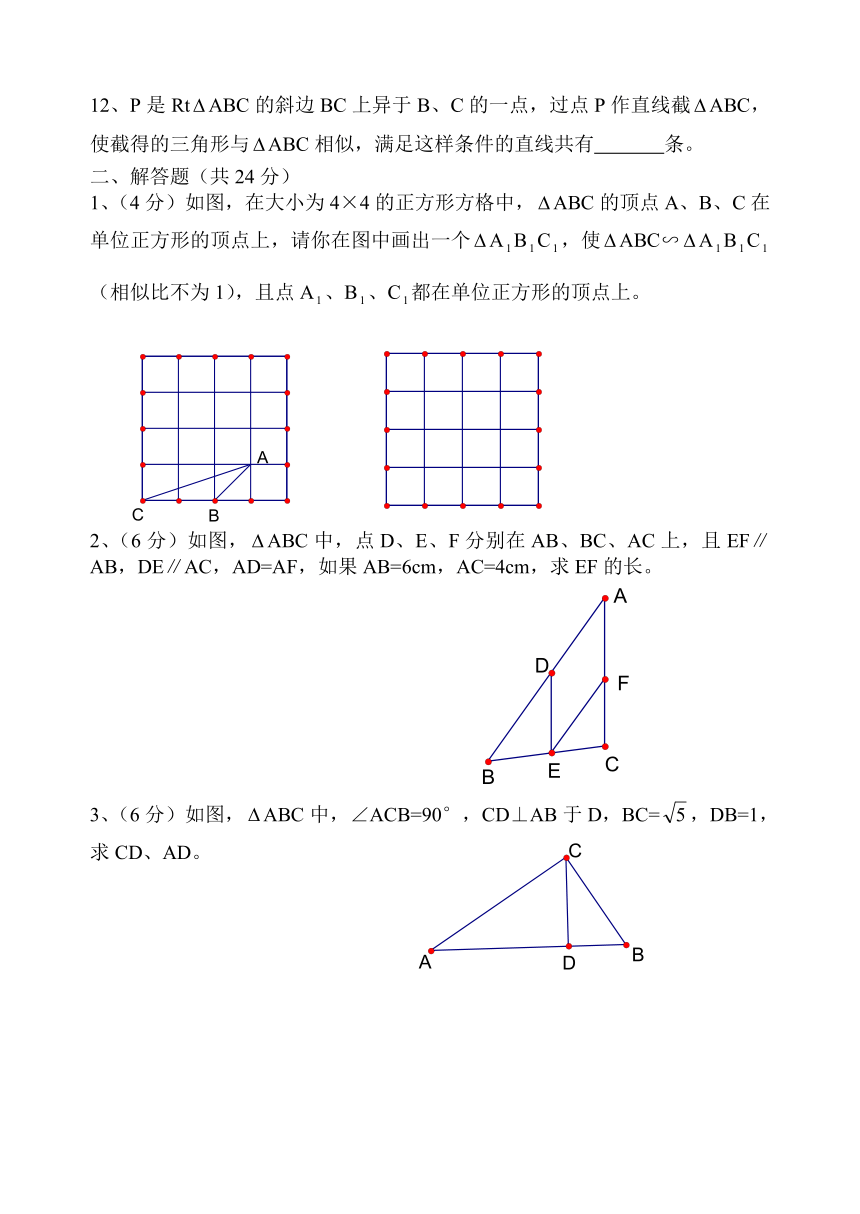
1、（4分）如图，在大小为4×4的正方形方格中，ABC的顶点A、B、C在单位正方形的顶点上，请你在图中画出一个ABC，使ABC∽ABC（相似比不为1），且点A、B、C都在单位正方形的顶点上。
2、（6分）如图，ABC中，点D、E、F分别在AB、BC、AC上，且EF∥AB，DE∥AC，AD=AF，如果AB=6cm，AC=4cm，求EF的长。
3、（6分）如图，ABC中，∠ACB=90°，CD⊥AB于D，BC=，DB=1，求CD、AD。
4、（8分）如图，ABC中，∠C=90°，P为AB上一点，且点P不与点A重合。过点P做PE⊥AB交AC边于E，点E不与点C重合。若AB=10，AC=8，设AP的长为x，四边形PECB的周长为y，试用含x的代数式表示y。
三、证明题（共18分）
1、（6分）已知：如图，ABC中，直线DF交AB于E，交BC于F，且BD=CE。
求证：AC·EF=AB·DF。
2、（6分）如图，ABC中D是AB上一点，E是AC上一点，且AB·AD=AC。求证：∠ACD=∠B。
3、（6分）如图，AC⊥DB，DE⊥AB。求证：。
3、 综合题（10分）
在公路的一侧有A、B两个村庄，它们都有垂直于公路的小路，长度分别是48米和30米，设两条小路相距130米。现在要在公路边上建一个供水站C，把水送到A、B两个村庄去，且使供水管最短。
1） 在图中找出供水站的位置C。（简述过程）
2） 求出点C到点E的距离。
选做题（10分）
如图，在平面直角坐标系内，已知点A（0，6），点B（8，0），动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动，同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动，设点P、点Q移动的时间为t秒。
1、求直线AB的解析式。
2、当t为何值时，AOB与以A、P、Q为顶点的三角形相似，并求出此时点P和点Q的坐标。
E
第4题图
第5题图
第10题图
第11题图
E
D