数学:2.3.1《抛物线及标准方程》ppt课件(新人教版a选修1-1)
文档属性
| 名称 | 数学:2.3.1《抛物线及标准方程》ppt课件(新人教版a选修1-1) |

|
|
| 格式 | rar | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-09 14:37:00 | ||
图片预览








文档简介
课件26张PPT。2.3.1《抛物线及标准方程》教学目标 知识与技能目标
使学生掌握抛物线的定义、抛物线的标准方程及其推导过程.
要求学生进一步熟练掌握解析几何的基本思想方法,提高分析、对比、概括、转化等方面的能力.
过程与方法目标
情感,态度与价值观目标
(1)培养学生用对称的美学思维来体现数学的和谐美。
(2)培养学生观察,实验,探究与交流的数学活动能力。能力目标:
(1)重视基础知识的教学、基本技能的训练和能力的培养;
(2)启发学生能够发现问题和提出问题,善于独立思考,学会分析问题和创造地解决问题;
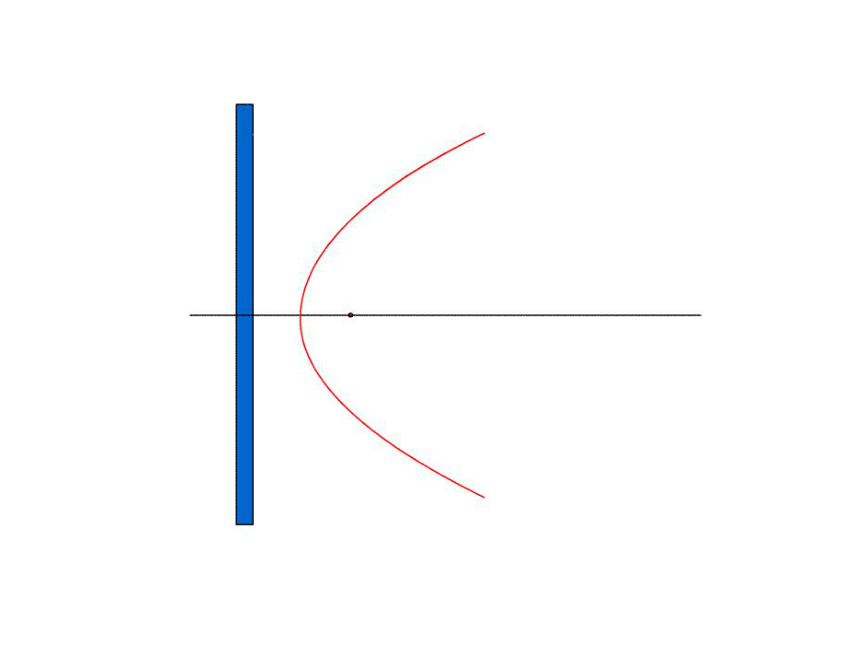
(3)通过教师指导发现知识结论,培养学生抽象概括能力和逻辑思维能力 与一个定点的距离和一条定直线的距离的比是常数e的点的轨迹椭圆思考是什么 ?双曲线(0 1) 图8-19 平面内与一个定点F和一条定直线L的距离相等的点的轨迹叫做抛物线。点F叫做抛物线的焦点,直线L叫做抛物线的准线。 抛物线的定义抛物线的标准方程 如图8-20,建立
直角坐标系xOy,使x轴经过点F且垂直于直线L,垂足为K,并使原点与线段KF的中点重合。
设|KF|= ( >0),那么焦点F的坐标为
( ),准线L的方程为x= - 抛物线的标准方程 设点M(x,y)是抛物线上任意一点,点M到L的距离为d。由抛物线的定义,抛物线就是集合 P={M|MF|=d}。 转化出关于 x .y的等式化简得抛物线的方程 方程①叫做抛物线的标准方程.它表示的抛物线的焦点在x轴的正半轴上,坐标是( ),它的准线方程是x= - 设|KF|= ( >0),
M(x,y)是抛物线上任意
一点,点M到L的距离为d,
由抛物线的定义,抛物线
就是集合P={M|MF|=d},
② 例1(1)已知抛物线的标准方程是y2=6x, 求它的焦点坐标和准线方程; (2)已知抛物线的焦点坐标是F(0,-2), 求它的标准方程。 例题1、根据下列条件写出抛物线的标准方程: (1)焦点是F(3,0); (2)准线方程是x=- ;(3)焦点到准线的距离是2; y2=12x y2=x
y2=4x , y2=-4x , x2=4y , x2=-4y练习 已知抛物线的方程是x2 +4y=0, 求它的焦点坐标和准线方程. 例题 解:
把 抛物线的方程x2 +4y=0化为标准方程,
x2 =-4y.
所以p=2,
焦点坐标是(0,-1),
准线方程是 y = 1 2、求下列抛物线的焦点坐标和准线方程: F(0 , -2) , y=2 ;
练习F(5,0),x=-5变式训练(A) y2 = - 4x1 . 选择题:
(1) 准线方程为x=2的抛物线的标准方程是( )(B) y2 = - 8x(D) y2 = 8x(C) y2 = 4x(2) 抛物线x2 +y=0 的焦点位于 ( )(A) x轴的负半轴上(B) x轴的正半轴上(D) y轴的正半轴上(C) y轴的负半轴上BC2 . 填空题:
(1) 焦点在直线3x-4y-12=0上的抛物线
的标准方程为 经过点(-8,8)的抛物线的标准方程为 y2 = 16x 或 x2 = -12x y2 = -8x 或 x2 = 8y1 . 解:设直线与x轴,y轴交于点F1、F2 ,
将y=0或x=0分别代入直线方程可解得
F1(4,0),F2(0,3),故所求抛物线
方程为:
y2=16x 或 x2=-12y
2 . 解:因为点(-8,8)在第二象限,所以
抛物线开口向上或者开口向左,设抛
物线方程为y2=-2P1x或x2=2P2y,由x=-8时,
y=8得:P1=4,P2=4,
所以:所求抛物线方程为:
y2= - 8x 或 x2= 8y 1? . 抛物线的定义 :
平面内与一个定点F和一条定直线L的
距离相等的点的轨迹叫做 抛物线 .点F叫
做抛物线的焦点,直线L叫做抛物线的准线.
小结2 .抛物线的图形及其标准方程
求抛物线y =4ax的焦点坐标和准线方程。 2
布置作业思考题再见
使学生掌握抛物线的定义、抛物线的标准方程及其推导过程.
要求学生进一步熟练掌握解析几何的基本思想方法,提高分析、对比、概括、转化等方面的能力.
过程与方法目标
情感,态度与价值观目标
(1)培养学生用对称的美学思维来体现数学的和谐美。
(2)培养学生观察,实验,探究与交流的数学活动能力。能力目标:
(1)重视基础知识的教学、基本技能的训练和能力的培养;
(2)启发学生能够发现问题和提出问题,善于独立思考,学会分析问题和创造地解决问题;
(3)通过教师指导发现知识结论,培养学生抽象概括能力和逻辑思维能力 与一个定点的距离和一条定直线的距离的比是常数e的点的轨迹椭圆思考是什么 ?双曲线(0
直角坐标系xOy,使x轴经过点F且垂直于直线L,垂足为K,并使原点与线段KF的中点重合。
设|KF|= ( >0),那么焦点F的坐标为
( ),准线L的方程为x= - 抛物线的标准方程 设点M(x,y)是抛物线上任意一点,点M到L的距离为d。由抛物线的定义,抛物线就是集合 P={M|MF|=d}。 转化出关于 x .y的等式化简得抛物线的方程 方程①叫做抛物线的标准方程.它表示的抛物线的焦点在x轴的正半轴上,坐标是( ),它的准线方程是x= - 设|KF|= ( >0),
M(x,y)是抛物线上任意
一点,点M到L的距离为d,
由抛物线的定义,抛物线
就是集合P={M|MF|=d},
② 例1(1)已知抛物线的标准方程是y2=6x, 求它的焦点坐标和准线方程; (2)已知抛物线的焦点坐标是F(0,-2), 求它的标准方程。 例题1、根据下列条件写出抛物线的标准方程: (1)焦点是F(3,0); (2)准线方程是x=- ;(3)焦点到准线的距离是2; y2=12x y2=x
y2=4x , y2=-4x , x2=4y , x2=-4y练习 已知抛物线的方程是x2 +4y=0, 求它的焦点坐标和准线方程. 例题 解:
把 抛物线的方程x2 +4y=0化为标准方程,
x2 =-4y.
所以p=2,
焦点坐标是(0,-1),
准线方程是 y = 1 2、求下列抛物线的焦点坐标和准线方程: F(0 , -2) , y=2 ;
练习F(5,0),x=-5变式训练(A) y2 = - 4x1 . 选择题:
(1) 准线方程为x=2的抛物线的标准方程是( )(B) y2 = - 8x(D) y2 = 8x(C) y2 = 4x(2) 抛物线x2 +y=0 的焦点位于 ( )(A) x轴的负半轴上(B) x轴的正半轴上(D) y轴的正半轴上(C) y轴的负半轴上BC2 . 填空题:
(1) 焦点在直线3x-4y-12=0上的抛物线
的标准方程为 经过点(-8,8)的抛物线的标准方程为 y2 = 16x 或 x2 = -12x y2 = -8x 或 x2 = 8y1 . 解:设直线与x轴,y轴交于点F1、F2 ,
将y=0或x=0分别代入直线方程可解得
F1(4,0),F2(0,3),故所求抛物线
方程为:
y2=16x 或 x2=-12y
2 . 解:因为点(-8,8)在第二象限,所以
抛物线开口向上或者开口向左,设抛
物线方程为y2=-2P1x或x2=2P2y,由x=-8时,
y=8得:P1=4,P2=4,
所以:所求抛物线方程为:
y2= - 8x 或 x2= 8y 1? . 抛物线的定义 :
平面内与一个定点F和一条定直线L的
距离相等的点的轨迹叫做 抛物线 .点F叫
做抛物线的焦点,直线L叫做抛物线的准线.
小结2 .抛物线的图形及其标准方程
求抛物线y =4ax的焦点坐标和准线方程。 2
布置作业思考题再见
