《直线与圆的位置关系》教案
文档属性
| 名称 | 《直线与圆的位置关系》教案 |

|
|
| 格式 | rar | ||
| 文件大小 | 32.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-07 00:00:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
《直线与圆的位置关系》教案
教学目标
知识与技能:
(1)了解直线和圆的位置关系的有关概念.
(2)理解设⊙O的半径为r,直线L到圆心O的距离为d,则有:直线L和⊙O相交dr.
(3)理解切线的判定定理:理解切线的性质定理并熟练掌握以上内容解决一些实际问题.复习点和圆的位置关系,引入直线和圆的位置关系,以直线和圆的位置关系中的d=r直线和圆相切,讲授切线的判定定理和性质定理
情感与态度:通过实际问题的解决提高学生分析问题的能力,激发学生的学习
热情,体会数学与现实生活的密切联系.
重难点、关键
1.重点:切线的判定定理;切线的性质定理及其运用它们解决一些具体的题目.
2.难点与关键:由上节课点和圆的位置关系迁移并运动直线导出直线和圆的
位置关系的三个对应等价
教学过程:
一、复习引入
(老师口问,学生口答,老师并在黑板上板书)同学们,我们前一节课已经学到点和圆的位置关系.设⊙O的半径为r,点P到圆心的距离OP=d,
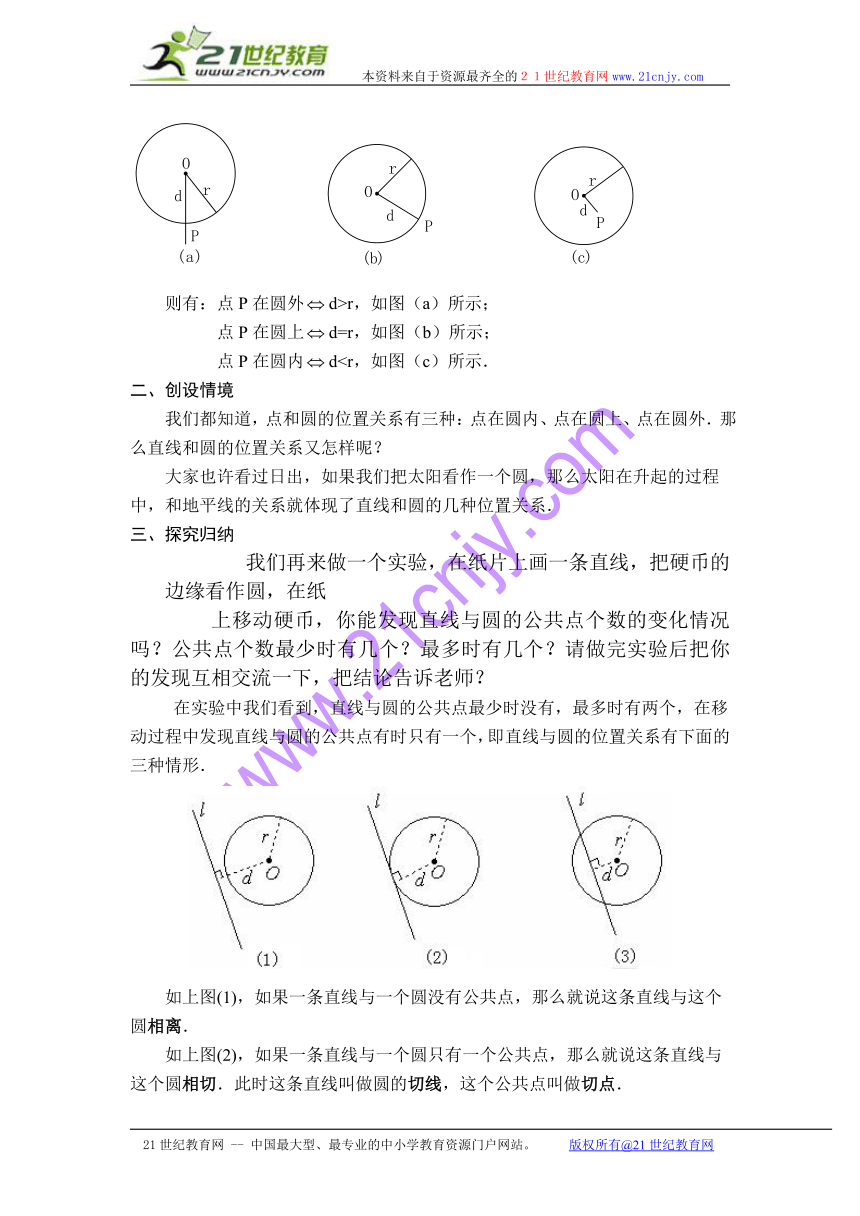
则有:点P在圆外d>r,如图(a)所示;
点P在圆上d=r,如图(b)所示;
点P在圆内d二、创设情境
我们都知道,点和圆的位置关系有三种:点在圆内、点在圆上、点在圆外.那
么直线和圆的位置关系又怎样呢?
大家也许看过日出,如果我们把太阳看作一个圆,那么太阳在升起的过程
中,和地平线的关系就体现了直线和圆的几种位置关系.
三、探究归纳
我们再来做一个实验,在纸片上画一条直线,把硬币的边缘看作圆,在纸
上移动硬币,你能发现直线与圆的公共点个数的变化情况吗?公共点个数最少时有几个?最多时有几个?请做完实验后把你的发现互相交流一下,把结论告诉老师?
在实验中我们看到,直线与圆的公共点最少时没有,最多时有两个,在移
动过程中发现直线与圆的公共点有时只有一个,即直线与圆的位置关系有下面的三种情形.
如上图(1),如果一条直线与一个圆没有公共点,那么就说这条直线与这个
圆相离.
如上图(2),如果一条直线与一个圆只有一个公共点,那么就说这条直线与
这个圆相切.此时这条直线叫做圆的切线,这个公共点叫做切点.
如上图(3),如果一条直线与一个圆有两个公共点,那么就说这条直线与这
个圆相交.此时这条直线叫做圆的割线.
直线与圆的位置关系只有三种:相离、相切、相交.那么能否用数量关系
来表示直线与圆的位置关系呢?
从前面的图中已发现,设如上图(2),如果一条直线与一个圆只有一个公共
点,那么就说这条直线与这个圆相切.此时这条直线叫做圆的切线,这个公共点叫做切点.⊙O的半径为r,圆心到直线的距离为d,我们也可用d和r之间的大小关系来判断直线与圆的位置关系.
如上图(1)圆心O到直线l的距离d大于半径r,因而直线上的所有点到圆
心的距离都大于半径r,说明直线l在圆的外部,与圆没有公共点,因此当d>r时,直线与圆的位置关系是相离,反之,如果已知直线l与⊙O相离,则d>r.即: d>r直线与圆相离.
同理可知,d=r直线与圆相切.d<r直线与圆相交.
四、实践应用
例1 在△ABC中,AB=10cm,BC=6cm,AC=8cm,(1)若以C为圆心,4 cm长
为半径画⊙C,则⊙C与AB的位置关系怎样?(2)若要使AB与⊙C 相切,则⊙C
的半径应当是多少?(3)若要以AC为直径画⊙O,则⊙O与AB、BC的位置关系
分别怎样?
分析 判断⊙C与AB的位置关系应求出点C到AB的距离CD的长,然后再
与半径作比较,即可求出⊙C与AB的位置关系.而要求CD的长,可利用 △ABC的面积,但应首先 判断 △ABC 为直角三角形.
解 过C作CD⊥AB,垂足为D .
因为BC2+AC2=62+82=100,AB2=102=100,
所以BC2+AC2= AB2,故△ABC是直角三角形,根据三角形面积相等得:
(1) 若以C为圆心,4cm长为半径画⊙C ,因为4cm<4.8cm,所以⊙C与AB的
(2) 位置关系为相离.
(2)若要使AB与⊙C相切,则⊙C的半径应为4.8cm .
(3)若以AC为直径画⊙O,由于BC⊥AC,故⊙O与BC相切;⊙O与AB相交.
例2 在Rt△ABC中,∠C=90°,O是BC的中点,以O为圆心的圆与线段AB
有两个交点,若AC=3,BC=4,求半径r的取值范围.
分析: 过O作OH⊥AB,根据△ABC∽△BOH求出OH,即可求出半径r的
范围.
解 过O作OH⊥AB,垂足为H,又∠C=90°,所以Rt△ABC∽Rt△BOH,
例3 如图,△ABO中,OC⊥AB于C,∠AOC=∠B,AC=16cm,BC=4cm,⊙O的
半径为8cm,AB是⊙O的切线吗?试说明.
分析 根据直线与圆的位置关系可知,要得到AB是⊙O的切线,只需求出
OC=8cm.
解 因为OC⊥AB,∠AOC=∠B,Rt△AOC∽Rt△OBC,
又因为⊙O的半径为8cm,所以AB是⊙O的切线.
五、巩固练习
教材P102 练习,P103 练习
六、交流反思
本堂课我们探索了直线与圆的位置关系,有几种?是如何来判断的?
直线与圆有三种位置关系,分别是相离、相切、相交:
(1)如果一条直线与一个圆没有公共点,那么就说这条直线与这个圆相离;
(2)如果一条直线与一个圆只有一个公共点,那么就说这条直线与这个圆相
切.此时这条直线叫做圆的切线,这个公共点叫做切点;
(3)如果一条直线与一个圆有两个公共点,那么就说这条直线与这个圆相交.此
时这条直线叫做圆的割线.
我们用圆心与直线的距离与半径的大小关系来判断直线与圆的位置关系.设⊙O
的半径为r,圆心O到直线l的距离为d,则:
(1)d>r直线与圆相离;
(2)d=r直线与圆相切;
(3)d<r直线与圆相交.
复习:点与圆的位置关系
引入
用类似利用圆心与点的距离来研究点与圆位置的方法来研究直线与圆的位置关系。
通过课本中日出的三幅图片中太阳与地平线的关系判定直线与圆的三种位置关系
通过圆心与直线的距离来研究三种位置关系的特征和性质
例题讲解,练习
小结
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
《直线与圆的位置关系》教案
教学目标
知识与技能:
(1)了解直线和圆的位置关系的有关概念.
(2)理解设⊙O的半径为r,直线L到圆心O的距离为d,则有:直线L和⊙O相交d
(3)理解切线的判定定理:理解切线的性质定理并熟练掌握以上内容解决一些实际问题.复习点和圆的位置关系,引入直线和圆的位置关系,以直线和圆的位置关系中的d=r直线和圆相切,讲授切线的判定定理和性质定理
情感与态度:通过实际问题的解决提高学生分析问题的能力,激发学生的学习
热情,体会数学与现实生活的密切联系.
重难点、关键
1.重点:切线的判定定理;切线的性质定理及其运用它们解决一些具体的题目.
2.难点与关键:由上节课点和圆的位置关系迁移并运动直线导出直线和圆的
位置关系的三个对应等价
教学过程:
一、复习引入
(老师口问,学生口答,老师并在黑板上板书)同学们,我们前一节课已经学到点和圆的位置关系.设⊙O的半径为r,点P到圆心的距离OP=d,
则有:点P在圆外d>r,如图(a)所示;
点P在圆上d=r,如图(b)所示;
点P在圆内d
我们都知道,点和圆的位置关系有三种:点在圆内、点在圆上、点在圆外.那
么直线和圆的位置关系又怎样呢?
大家也许看过日出,如果我们把太阳看作一个圆,那么太阳在升起的过程
中,和地平线的关系就体现了直线和圆的几种位置关系.
三、探究归纳
我们再来做一个实验,在纸片上画一条直线,把硬币的边缘看作圆,在纸
上移动硬币,你能发现直线与圆的公共点个数的变化情况吗?公共点个数最少时有几个?最多时有几个?请做完实验后把你的发现互相交流一下,把结论告诉老师?
在实验中我们看到,直线与圆的公共点最少时没有,最多时有两个,在移
动过程中发现直线与圆的公共点有时只有一个,即直线与圆的位置关系有下面的三种情形.
如上图(1),如果一条直线与一个圆没有公共点,那么就说这条直线与这个
圆相离.
如上图(2),如果一条直线与一个圆只有一个公共点,那么就说这条直线与
这个圆相切.此时这条直线叫做圆的切线,这个公共点叫做切点.
如上图(3),如果一条直线与一个圆有两个公共点,那么就说这条直线与这
个圆相交.此时这条直线叫做圆的割线.
直线与圆的位置关系只有三种:相离、相切、相交.那么能否用数量关系
来表示直线与圆的位置关系呢?
从前面的图中已发现,设如上图(2),如果一条直线与一个圆只有一个公共
点,那么就说这条直线与这个圆相切.此时这条直线叫做圆的切线,这个公共点叫做切点.⊙O的半径为r,圆心到直线的距离为d,我们也可用d和r之间的大小关系来判断直线与圆的位置关系.
如上图(1)圆心O到直线l的距离d大于半径r,因而直线上的所有点到圆
心的距离都大于半径r,说明直线l在圆的外部,与圆没有公共点,因此当d>r时,直线与圆的位置关系是相离,反之,如果已知直线l与⊙O相离,则d>r.即: d>r直线与圆相离.
同理可知,d=r直线与圆相切.d<r直线与圆相交.
四、实践应用
例1 在△ABC中,AB=10cm,BC=6cm,AC=8cm,(1)若以C为圆心,4 cm长
为半径画⊙C,则⊙C与AB的位置关系怎样?(2)若要使AB与⊙C 相切,则⊙C
的半径应当是多少?(3)若要以AC为直径画⊙O,则⊙O与AB、BC的位置关系
分别怎样?
分析 判断⊙C与AB的位置关系应求出点C到AB的距离CD的长,然后再
与半径作比较,即可求出⊙C与AB的位置关系.而要求CD的长,可利用 △ABC的面积,但应首先 判断 △ABC 为直角三角形.
解 过C作CD⊥AB,垂足为D .
因为BC2+AC2=62+82=100,AB2=102=100,
所以BC2+AC2= AB2,故△ABC是直角三角形,根据三角形面积相等得:
(1) 若以C为圆心,4cm长为半径画⊙C ,因为4cm<4.8cm,所以⊙C与AB的
(2) 位置关系为相离.
(2)若要使AB与⊙C相切,则⊙C的半径应为4.8cm .
(3)若以AC为直径画⊙O,由于BC⊥AC,故⊙O与BC相切;⊙O与AB相交.
例2 在Rt△ABC中,∠C=90°,O是BC的中点,以O为圆心的圆与线段AB
有两个交点,若AC=3,BC=4,求半径r的取值范围.
分析: 过O作OH⊥AB,根据△ABC∽△BOH求出OH,即可求出半径r的
范围.
解 过O作OH⊥AB,垂足为H,又∠C=90°,所以Rt△ABC∽Rt△BOH,
例3 如图,△ABO中,OC⊥AB于C,∠AOC=∠B,AC=16cm,BC=4cm,⊙O的
半径为8cm,AB是⊙O的切线吗?试说明.
分析 根据直线与圆的位置关系可知,要得到AB是⊙O的切线,只需求出
OC=8cm.
解 因为OC⊥AB,∠AOC=∠B,Rt△AOC∽Rt△OBC,
又因为⊙O的半径为8cm,所以AB是⊙O的切线.
五、巩固练习
教材P102 练习,P103 练习
六、交流反思
本堂课我们探索了直线与圆的位置关系,有几种?是如何来判断的?
直线与圆有三种位置关系,分别是相离、相切、相交:
(1)如果一条直线与一个圆没有公共点,那么就说这条直线与这个圆相离;
(2)如果一条直线与一个圆只有一个公共点,那么就说这条直线与这个圆相
切.此时这条直线叫做圆的切线,这个公共点叫做切点;
(3)如果一条直线与一个圆有两个公共点,那么就说这条直线与这个圆相交.此
时这条直线叫做圆的割线.
我们用圆心与直线的距离与半径的大小关系来判断直线与圆的位置关系.设⊙O
的半径为r,圆心O到直线l的距离为d,则:
(1)d>r直线与圆相离;
(2)d=r直线与圆相切;
(3)d<r直线与圆相交.
复习:点与圆的位置关系
引入
用类似利用圆心与点的距离来研究点与圆位置的方法来研究直线与圆的位置关系。
通过课本中日出的三幅图片中太阳与地平线的关系判定直线与圆的三种位置关系
通过圆心与直线的距离来研究三种位置关系的特征和性质
例题讲解,练习
小结
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
