一元二次不等式及其解法

课件21张PPT。一元二次不等式及其解法 某同学要把自己的计算机接入因特网.现有两家ISP公司可供选择.公司A每小时收费1.5元;公司B的收费原则如下:在用户上网的第1小时内收费1.7元,第2小时内收费1.6元,以后每小时减少0.1元(若用户一次上网时间超过17小时,按17小时计算).
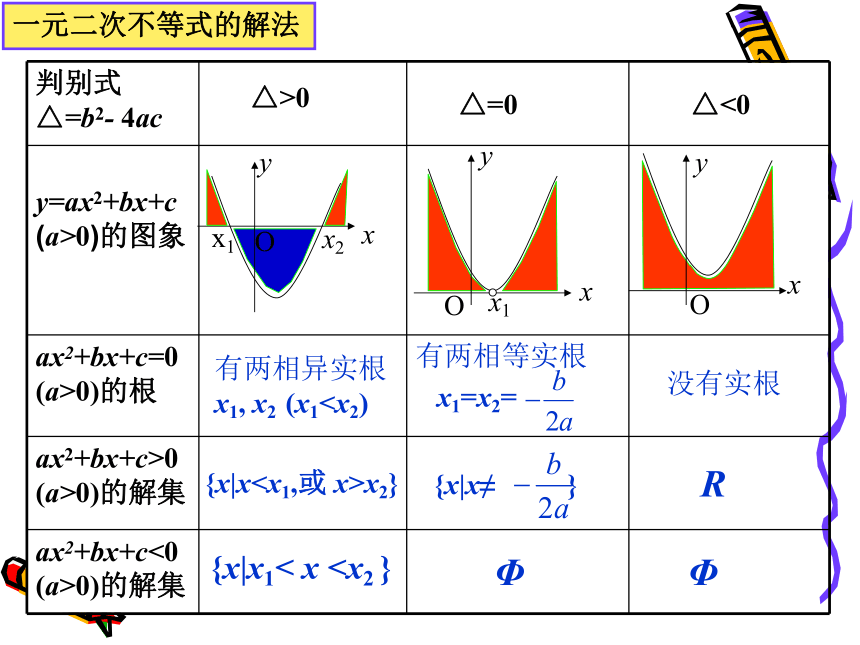
一般来说,一次上网时间不会超过17小时,所以,不妨假设一次上网时间总小于17小时.那么,一次上网在多长时间以内能够保证选择公司A比选择公司B所需费用少?△>0有两相异实根
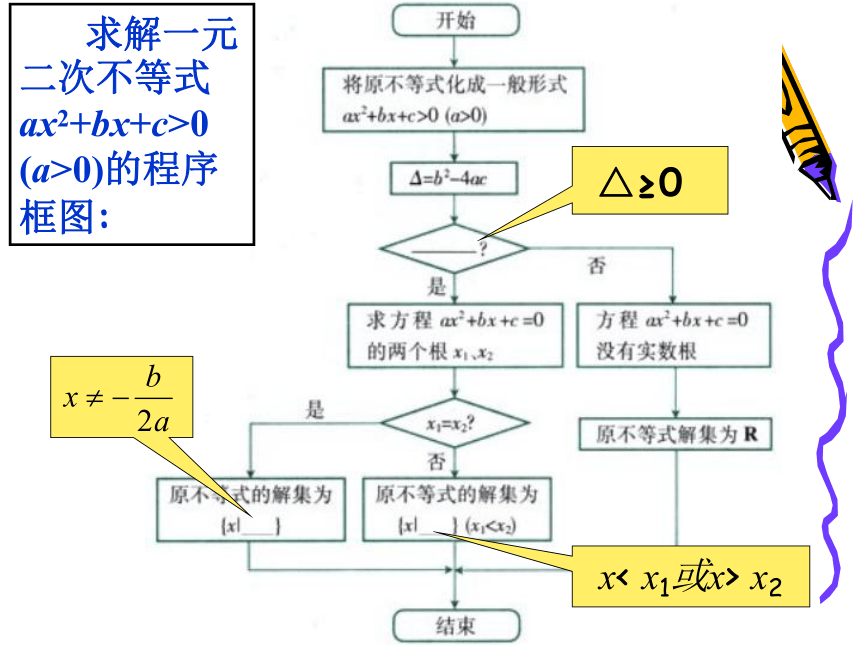
x1, x2 (x1x2}{x|x1< x x1=x2={x|x≠ }ΦΦR没有实根一元二次不等式的解法 求解一元二次不等式ax2+bx+c>0
(a>0)的程序框图:x< x1或x> x2另解： 因为△= 16 -16 =0 方程 4 x2 - 4x +1=0 的解是
x1=x2=1/2故原不等式的解集为{ x| x ≠ 1/2 }题3：解不等式- x2 + 2x – 3 >0 解：整理，得 x2 - 2x + 3 < 0因为△= 4 - 12 = - 8 < 0方程 2 x2 - 3x – 2 = 0无实数根所以原不等式的解集为ф题2：解不等式4x2-4x +1>0解:
由于4x2-4x+1=(2x-1)2≥0 解一元二次不等式ax2+bx+c>0、ax2+bx+c<0 (a>0) 的步骤是： (1)化成标准形式 ax2+bx+c>0 (a>0)
ax2+bx+c<0 (a>0)
(2)判定△与0的关系，并求出方程ax2+bx+c=0
的实根;
(3)写出不等式的解集.小结不等式ax2 +（a-1）x+ a-1＜0对所有实数x∈R都成立，求a的取值范围.分析：开口向下，且与x轴无交点 。
解：由题目条件知：
(1) a ＜ 0，且△ ＜ 0.
因此a ＜ -1/3。
（2）a = 0时，不等式为-x-1 ＜0
不符合题意。
综上所述：a的取值范围是 例4 一个车辆制造厂引进了一条摩托车整车装配流水线,这条流水线生产的摩托车数量x(辆)与创造的价值 y(元)之间有如下的关系: y = -2 x2 + 220x.
若这家工厂希望在一个星期内利用这条流水线创收6000元以上,那么它在一个星期内大约应该生产多少辆摩托车? 解:设在一个星期内大约应该生产x辆摩托车.根据题意,得到 -2x2 + 220x > 6000
移项整理,得 x2 - 110x + 3000 < 0.
因为△=100>0,所以方程 x2-110x+3000=0有两个实数根
x1=50, x2=60.
由函数y=x2-110x+3000的图象,
得不等式的解为50 因为x只能取整数,所以当这条摩托
车整车装配流水线在一周内生产的摩托
车数量在51辆到59辆之间时,这家工厂
能够获得6000元以上的收益.不等式ax2 +（a-1）x+ a-1＜0对所有实数x∈R都成立，求a的取值范围.分析：开口向下，且与x轴无交点 。
解：由题目条件知：
(1) a ＜ 0，且△ ＜ 0.
因此a ＜ -1/3。
（2）a = 0时，不等式为-x-1 ＜0
不符合题意。
综上所述：a的取值范围是二次不等式ax2+bx+c>0的解集是全体实数的条件是______.a>0时，⊿＝b2-4ac<0例2 解关于x的不等式(x-2)(ax-2)>0.答案要求得不等式cx2-bx+a<0的解集，需要做三件事，(1)确定c的正负情况；(2)求得与不等式相对应的方程cx2-bx+a＝0的根；(3)比较方程cx2-bx+a＝0两根的大小．而以上三件事的解决，可通过开发题设的内涵来完成作业P.89练习
第二题（1）（2）课后练习
第二题（3）（4）写在作业本
习题3.2第二题写在作业本设a≠b,解关于x的不等式： a2x+b2(1-x) ≥[ax-b(1-x)]2.解下列不等式①2x-a②
③分b>2；b<2；b=2三种情况