球的体积
图片预览







文档简介
(共22张PPT)
已知半径为R的球O,用过球心的平面去截球O,球被截面分成大小相等的两个半球,截面圆O(包含它内部的点),叫做所得半球的底面。
半球的底面
一、新课
R
O
O.
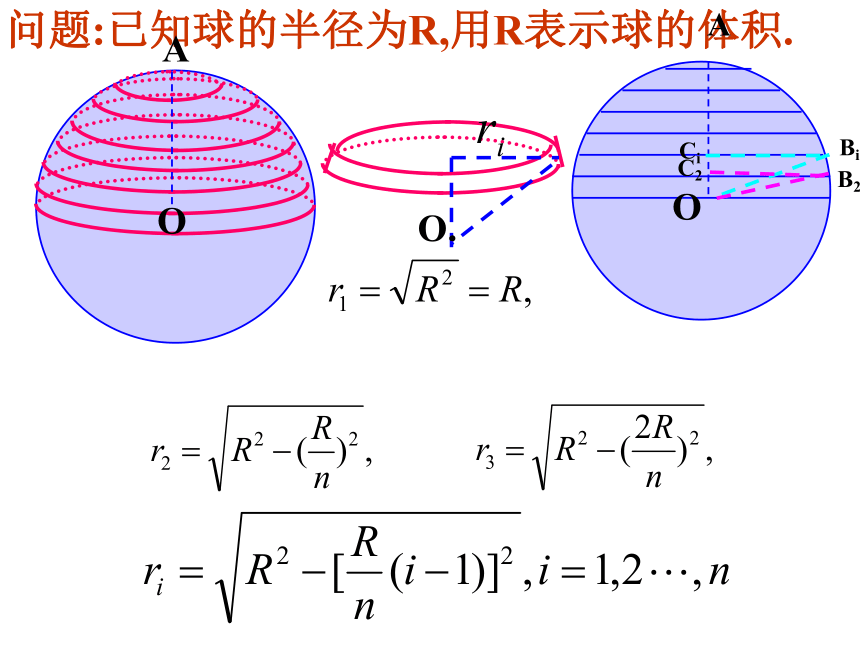
问题:已知球的半径为R,用R表示球的体积.
A
O
A
O
B2
C2
Bi
Ci
问题:已知球的半径为R,用R表示球的体积.
球的体积
R
定理:半径是R的球的体积
1.一种空心钢球的质量是142g,外径是5cm,求它的内径.(钢的密度是7.9g/cm2)
解:设空心钢球的内径为2xcm,则钢球的质量是
答:空心钢球的内径约为4.5cm.
由计算器算得:
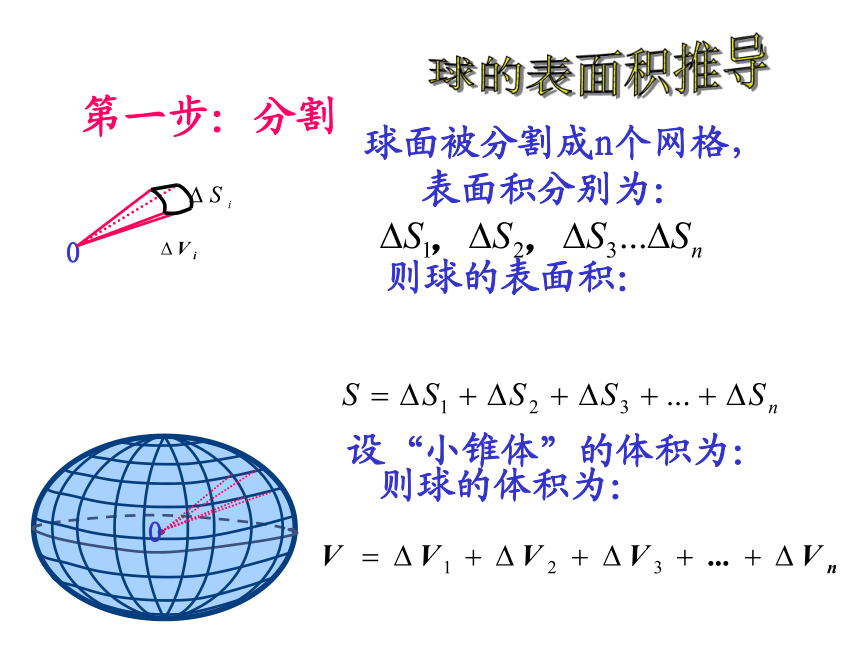
第一步:分割
球面被分割成n个网格,
表面积分别为:
则球的表面积:
O
则球的体积为:
设“小锥体”的体积为:
O
第二步:求近似和
O
由第一步得:
O
第三步:化为准确和
如果网格分的越细,则:
①
由①② 得:
②
球的体积:
的值就趋向于球的半径R
O
“小锥体”就越接近小棱锥。
球的表面积
定理:半径是R的球的表面积是
例1.钢球直径是5cm,求它的体积.
变式1.一种空心钢球的质量是142g,外径是5cm,求它的内径.(钢的密度是7.9g/cm2)
例1.钢球直径是5cm,求它的体积.
(变式2)把钢球放入一个正方体的有盖纸盒中,至少要用多少纸
用料最省时,球与正方体有什么位置关系
球内切于正方体
侧棱长为5cm
O
A
B
C
H
例3:A、B、C是球面上三点,已知弦AB=18cm,BC=24cm,AC=30cm,平面ABC与球心的距离恰好为球半径的一半,求球的表面积。
1.球的直径伸长为原来的2倍,体积变为原来的几倍
2.一个正方体的顶点都在球面上,它的棱长是4cm,求这个球的体积.
8倍
球外接于正方体
例1.一种空心钢球的质量是142g,外径是5cm,求它的内径.(钢的密度是7.9g/cm2)
(变式1)把钢球放入一个正方体的有盖纸盒中,至少要用多少纸
(变式3)把正方体的纸盒装入半径为4cm的球状木盒里,能否装得下
半径为4cm的木盒能装下的最大正方体与球盒有什么位置关系
球外接于正方体
3.有三个球,一球切于正方体的各面,一球切于正方体的各侧棱,一球过正方体的各顶点,求这三个球的体积之比.
作轴截面
4.求球与它的外切圆柱、外切等边圆锥的体积之比。
4.求球与它的外切圆柱、外切等边圆锥的体积之比。
(变式)一个倒等边圆锥形容器,将一个半径为r的铁球放入其中,并向容器内注水,使水面恰与铁球相切,将球取出后,容器内的水深为多少
1.两种方法:化整为零的思想方法和“分割,求和,取极限”的数学方法.
2.一个观点:在一定条件下,化曲为直的辨证观点.
3.一个公式:半径为R的球的体积是
4.解决两类问题:两个几何体相切和相接
作适当的轴截面
两个几何体相切:一个几何体的各个面与另一个几何体的各面相切.
两个几何体相接:一个几何体的所有顶点都 在另一个几何体的表面上
已知半径为R的球O,用过球心的平面去截球O,球被截面分成大小相等的两个半球,截面圆O(包含它内部的点),叫做所得半球的底面。
半球的底面
一、新课
R
O
O.
问题:已知球的半径为R,用R表示球的体积.
A
O
A
O
B2
C2
Bi
Ci
问题:已知球的半径为R,用R表示球的体积.
球的体积
R
定理:半径是R的球的体积
1.一种空心钢球的质量是142g,外径是5cm,求它的内径.(钢的密度是7.9g/cm2)
解:设空心钢球的内径为2xcm,则钢球的质量是
答:空心钢球的内径约为4.5cm.
由计算器算得:
第一步:分割
球面被分割成n个网格,
表面积分别为:
则球的表面积:
O
则球的体积为:
设“小锥体”的体积为:
O
第二步:求近似和
O
由第一步得:
O
第三步:化为准确和
如果网格分的越细,则:
①
由①② 得:
②
球的体积:
的值就趋向于球的半径R
O
“小锥体”就越接近小棱锥。
球的表面积
定理:半径是R的球的表面积是
例1.钢球直径是5cm,求它的体积.
变式1.一种空心钢球的质量是142g,外径是5cm,求它的内径.(钢的密度是7.9g/cm2)
例1.钢球直径是5cm,求它的体积.
(变式2)把钢球放入一个正方体的有盖纸盒中,至少要用多少纸
用料最省时,球与正方体有什么位置关系
球内切于正方体
侧棱长为5cm
O
A
B
C
H
例3:A、B、C是球面上三点,已知弦AB=18cm,BC=24cm,AC=30cm,平面ABC与球心的距离恰好为球半径的一半,求球的表面积。
1.球的直径伸长为原来的2倍,体积变为原来的几倍
2.一个正方体的顶点都在球面上,它的棱长是4cm,求这个球的体积.
8倍
球外接于正方体
例1.一种空心钢球的质量是142g,外径是5cm,求它的内径.(钢的密度是7.9g/cm2)
(变式1)把钢球放入一个正方体的有盖纸盒中,至少要用多少纸
(变式3)把正方体的纸盒装入半径为4cm的球状木盒里,能否装得下
半径为4cm的木盒能装下的最大正方体与球盒有什么位置关系
球外接于正方体
3.有三个球,一球切于正方体的各面,一球切于正方体的各侧棱,一球过正方体的各顶点,求这三个球的体积之比.
作轴截面
4.求球与它的外切圆柱、外切等边圆锥的体积之比。
4.求球与它的外切圆柱、外切等边圆锥的体积之比。
(变式)一个倒等边圆锥形容器,将一个半径为r的铁球放入其中,并向容器内注水,使水面恰与铁球相切,将球取出后,容器内的水深为多少
1.两种方法:化整为零的思想方法和“分割,求和,取极限”的数学方法.
2.一个观点:在一定条件下,化曲为直的辨证观点.
3.一个公式:半径为R的球的体积是
4.解决两类问题:两个几何体相切和相接
作适当的轴截面
两个几何体相切:一个几何体的各个面与另一个几何体的各面相切.
两个几何体相接:一个几何体的所有顶点都 在另一个几何体的表面上
