同底数幂的除法
图片预览






文档简介
课件14张PPT。第十三章 整式的乘除
同底数幂的除法
1.本课提要
2.课前小测
3.典型问题
4.技能训练
5.变式训练
8年级上册本课提要 课前小测从复习同底数幂乘法运算的法则入手,帮助同学在回顾旧知识的过程中为接纳新知识作了必要的铺垫.典型问题1、2、3由浅入深、层层相扣,引导同学们探索同底数幂除法运算的法则及其用法,注重知识形成的过程.技能训练和变式训练能较好地弥补教材练习题少、习题梯度跳跃的问题,提醒同学们注意比较习题中含有符号变化的题目. 课前小测
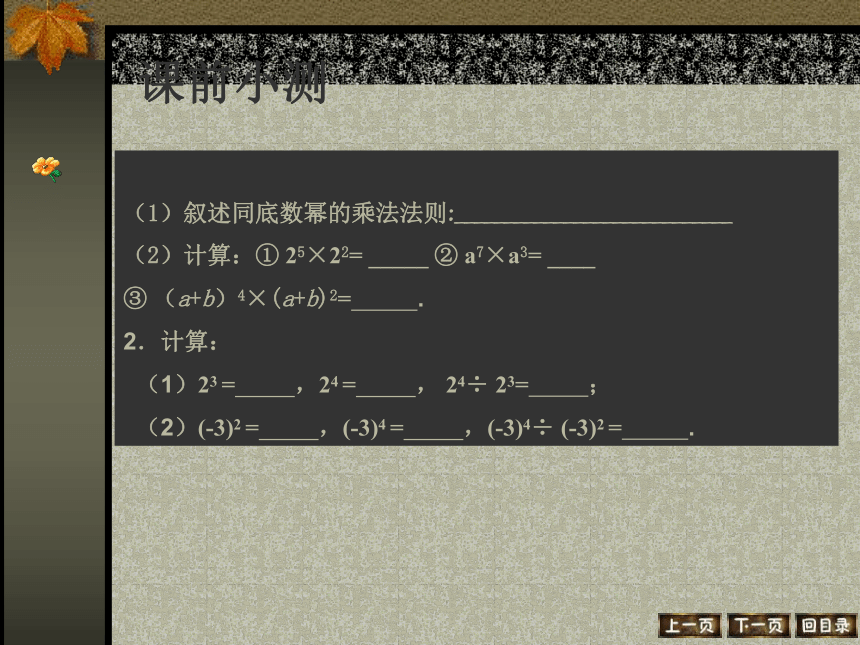
(1)叙述同底数幂的乘法法则:____________________________
(2)计算:① 25×22=?_____ ② a7×a3=?____
③ (a+b)4×(a+b)2= .
2.计算:
(1)23 = ,24 = , 24÷ 23= ;
(2)(-3)2 = ,(-3)4 = ,(-3)4÷ (-3)2 = .典型问题问题一
问题二
问题三
【问题1】试一试,用你熟悉的方法计算:
(1)25 ÷ 22 =_________________________= 2( ) ;
(2)107 ÷ 103 = = 5( );
(3)a7 ÷ a3 = = a( );
结论1:同底数幂相除, 不变,指数 .
即am ÷ an = (m、n为正整数) .底数 相减 am-n当m,n都是正整数时,如何计算呢?
am÷an=?
an·(? )= am
∵ an·am-n=an+(m-n) =am,
∴ am ÷ an = .
am-n同底数幂除法运算法则
同底数幂相除, 不变,指数 .
即am ÷ an = (m、n为正整数) .
底数 相减 am-n练一练: 3. 判断下列计算是否正确,如果不正确,请给出正确答案.
(1) a2 ÷ a = a2;
(2)a+a2 = a3;
(3)a3 · a3 = a6;
(4)a3+a3 = a6.
4. 填空:
(1)108 ÷ 104 = 10( );
(2)( b )6÷( )2 = ( b )( )解:错,结果应为a ;解:错,a+a2已是最后结果,不能再化简 ;解:正确 解:错,结果应为2a3.7 【问题2】在运算过程当中,除数能否为0?
计算(结果以幂的形式表示):
(1)68 ÷ 65 = ______________;
(2)a5 ÷ a5 = _________ ;
(3) (a+b)3 ÷ (a+b) =__________.
结论2:an ÷an=1 (a不为0) 底数可表示非零数,或字母或单项式、多项式(均不能为零)。计算(结果以幂的形式表示):
(1)211 ÷ 23 ÷ 24=___________________________;
(2)a8 ÷ a2 ÷ a5 =________________________;
(3)(x-y)7 ÷(x-y) ÷(x-y)3 = ________________
结论3【问题3】 am÷an ÷ap =am-n-p
(m、n 、p为正整数,a不为0) 计算下列各式(结果以幂的形式表示):
1.(1)109 ÷ 105; (2)a8 ÷ a7.
2.(1)76 ÷ 73 ÷ 73; (2)x7 ÷ (x6 ÷ x4 ).
3.(1)104×105 ÷ 105; (2)x 4÷ x5·x7.
技能训练 4.(1)(a+b)6 ÷(a+b)2; (2)(x-y)8÷(x-y)5.
5.(1)311÷ 27; (2)516 ÷ 125.
6.(1)915 ÷(-95) ÷(-9); (2)( -b )4 ÷(- b 2 ) ÷ b.=(a+b)4=(x-y)3=38=513=99=-b 7.(1)(x-y) 11÷(x-y)2 ÷(x-y)3;
(2)(a+b)9÷(a+b)2 ÷(-a-b).
8.(1)(m-n)5÷(n-m);
(2)(a-b)8 ÷(b-a) ÷(b-a).=(x-y)6=-(a+b)6=-(m-n)4=(a-b)69. 计算:
(1)(– 2)6 ÷(– 2)2–(– 2)7÷(– 2)3;
(2)y 10÷ y2 ÷ y3+y9 ÷ y4 – 3y3y2.变式训练 10. 如果x2m-1 ÷ x2 =xm+1,求m的值.
11. 若10m=16,10n=20,求10m-n的值. 解:∵ x2m-1 ÷ x2 =xm+1 ,
∴2m-1-2=m+1,
解得:m=4.解:∵ 10m =16,10n=20,
∴ 10m-n =10m ÷ 10n =16 ÷ 20=0.8
同底数幂的除法
1.本课提要
2.课前小测
3.典型问题
4.技能训练
5.变式训练
8年级上册本课提要 课前小测从复习同底数幂乘法运算的法则入手,帮助同学在回顾旧知识的过程中为接纳新知识作了必要的铺垫.典型问题1、2、3由浅入深、层层相扣,引导同学们探索同底数幂除法运算的法则及其用法,注重知识形成的过程.技能训练和变式训练能较好地弥补教材练习题少、习题梯度跳跃的问题,提醒同学们注意比较习题中含有符号变化的题目. 课前小测
(1)叙述同底数幂的乘法法则:____________________________
(2)计算:① 25×22=?_____ ② a7×a3=?____
③ (a+b)4×(a+b)2= .
2.计算:
(1)23 = ,24 = , 24÷ 23= ;
(2)(-3)2 = ,(-3)4 = ,(-3)4÷ (-3)2 = .典型问题问题一
问题二
问题三
【问题1】试一试,用你熟悉的方法计算:
(1)25 ÷ 22 =_________________________= 2( ) ;
(2)107 ÷ 103 = = 5( );
(3)a7 ÷ a3 = = a( );
结论1:同底数幂相除, 不变,指数 .
即am ÷ an = (m、n为正整数) .底数 相减 am-n当m,n都是正整数时,如何计算呢?
am÷an=?
an·(? )= am
∵ an·am-n=an+(m-n) =am,
∴ am ÷ an = .
am-n同底数幂除法运算法则
同底数幂相除, 不变,指数 .
即am ÷ an = (m、n为正整数) .
底数 相减 am-n练一练: 3. 判断下列计算是否正确,如果不正确,请给出正确答案.
(1) a2 ÷ a = a2;
(2)a+a2 = a3;
(3)a3 · a3 = a6;
(4)a3+a3 = a6.
4. 填空:
(1)108 ÷ 104 = 10( );
(2)( b )6÷( )2 = ( b )( )解:错,结果应为a ;解:错,a+a2已是最后结果,不能再化简 ;解:正确 解:错,结果应为2a3.7 【问题2】在运算过程当中,除数能否为0?
计算(结果以幂的形式表示):
(1)68 ÷ 65 = ______________;
(2)a5 ÷ a5 = _________ ;
(3) (a+b)3 ÷ (a+b) =__________.
结论2:an ÷an=1 (a不为0) 底数可表示非零数,或字母或单项式、多项式(均不能为零)。计算(结果以幂的形式表示):
(1)211 ÷ 23 ÷ 24=___________________________;
(2)a8 ÷ a2 ÷ a5 =________________________;
(3)(x-y)7 ÷(x-y) ÷(x-y)3 = ________________
结论3【问题3】 am÷an ÷ap =am-n-p
(m、n 、p为正整数,a不为0) 计算下列各式(结果以幂的形式表示):
1.(1)109 ÷ 105; (2)a8 ÷ a7.
2.(1)76 ÷ 73 ÷ 73; (2)x7 ÷ (x6 ÷ x4 ).
3.(1)104×105 ÷ 105; (2)x 4÷ x5·x7.
技能训练 4.(1)(a+b)6 ÷(a+b)2; (2)(x-y)8÷(x-y)5.
5.(1)311÷ 27; (2)516 ÷ 125.
6.(1)915 ÷(-95) ÷(-9); (2)( -b )4 ÷(- b 2 ) ÷ b.=(a+b)4=(x-y)3=38=513=99=-b 7.(1)(x-y) 11÷(x-y)2 ÷(x-y)3;
(2)(a+b)9÷(a+b)2 ÷(-a-b).
8.(1)(m-n)5÷(n-m);
(2)(a-b)8 ÷(b-a) ÷(b-a).=(x-y)6=-(a+b)6=-(m-n)4=(a-b)69. 计算:
(1)(– 2)6 ÷(– 2)2–(– 2)7÷(– 2)3;
(2)y 10÷ y2 ÷ y3+y9 ÷ y4 – 3y3y2.变式训练 10. 如果x2m-1 ÷ x2 =xm+1,求m的值.
11. 若10m=16,10n=20,求10m-n的值. 解:∵ x2m-1 ÷ x2 =xm+1 ,
∴2m-1-2=m+1,
解得:m=4.解:∵ 10m =16,10n=20,
∴ 10m-n =10m ÷ 10n =16 ÷ 20=0.8
