课题:13.3.1整式乘法复习(华东师大)
文档属性
| 名称 | 课题:13.3.1整式乘法复习(华东师大) |
|
|
| 格式 | rar | ||
| 文件大小 | 13.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-12 09:27:00 | ||
图片预览



文档简介
课题:13.3.1整式乘法复习
执笔人:仝蒙蒙 审核人:刘淑玲 使用时间:
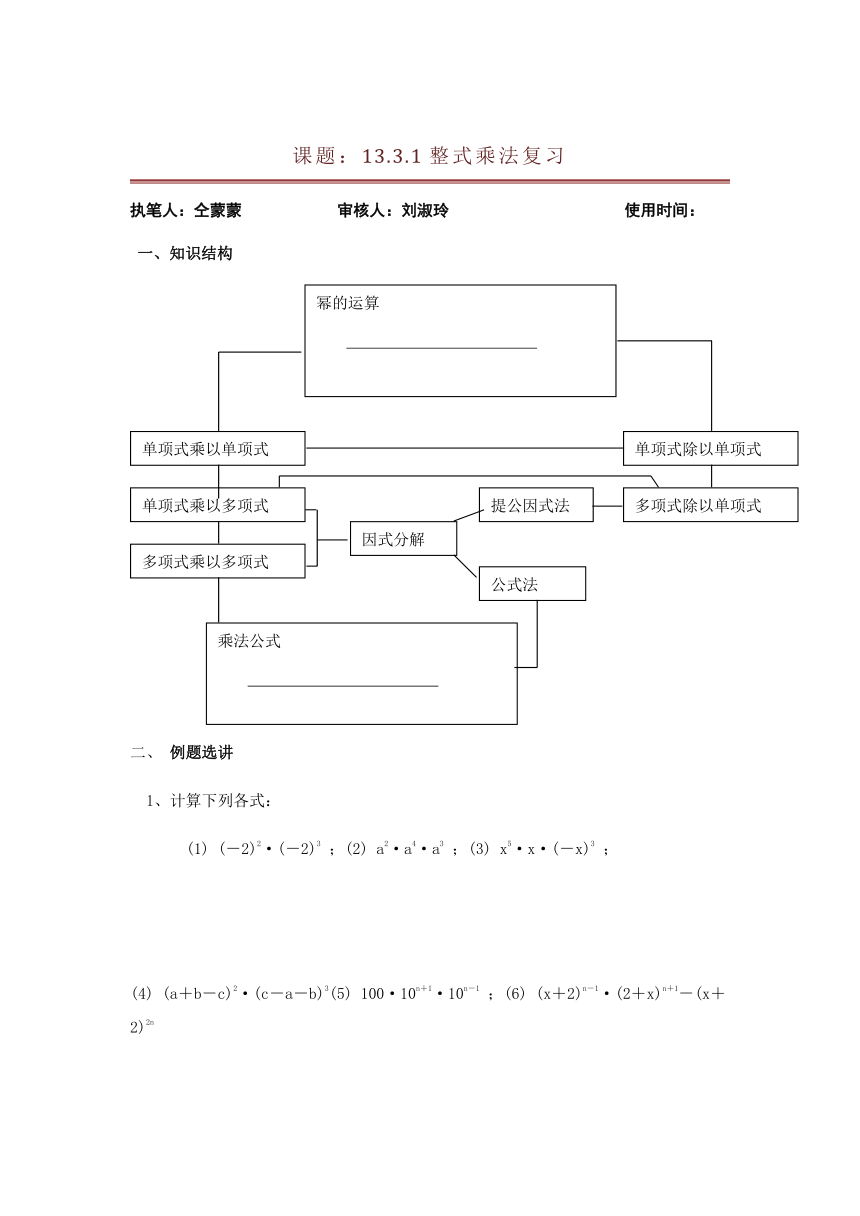
一、知识结构
二、 例题选讲
1、计算下列各式:
(1) (-2)2·(-2)3 ;(2) a2·a4·a3 ;(3) x5·x·(-x)3 ;
(4) (a+b-c)2·(c-a-b)3(5) 100·10n+1·10n-1 ;(6) (x+2)n-1·(2+x)n+1-(x+2)2n
解题方法:熟记公式是解这类题的前提,当题中幂的底数不同时,必须利用乘法和乘方的意义变形,化成同底数幂;当题目中有加、减、乘混合运算时,应计算同底数幂的乘法,然后再合并同类项.
2、计算下列各式:
(1) [(-2)2]6 ;(2) [(x+y)3]4 ;(3) (a4n)n-1 ;(4) -(y4)2·(y2)3 ;
(5) (-a3)2+(-a2)3-(-a2)·(-a)4 ;(6) x3·x2·x4+(-x4)2+4(-x2)4
3、计算下列各式:
(1) (-3a4)3 ; (2) (a2b3)m ;
(3) [(x+y)(x-y)]5 ; (4) (x m+2·y 2n-1)2 ;
(5) (-0.125)8×225 ;(6) (1990)n·()n+1 ;
4、已知22x+1+4x=48,求x的值.
解题方法:解这种有关指数方程的基本方法是,将左右两边变形为两个幂相等的等式,且左右两边幂的底数相同,再根据两个底数相同的幂相等,其指数必定相等列出方程,解这个方程即可.
三、课堂练习
1、计算:
(1) 3x2y·(-2xy3) (2) (-5a2b3)·(-4b2c)·a2b
2、计算:
(1) (-2a2)·(3ab2-5ab3) (2) (-2x2y)2(-y2+xy+x3)
3、已知x+y=4,x-y=6,求代数式x y(y2+y)-y2(x y+2x)-3x y的值
4、计算:
(1) (3x2-2x-5)(-2x+3) (2) (2x-y)(4x2+2xy+y2)
(3) (3a+2b)2 (4) (x-1)(2x-3)(3x+1)
5、已知(a2+pa+8)与(a2-3a+q)的乘积中不含a3和a2项,求p、q的值.
分析:不含有这个项,即为此项的系数为零,又(a2+pa+8)与(a2-3a+q)的乘积中的a3项是-3a3+pa3=(-3+p)a3, a2项是qa2-3pa2+8a2=(q-3 p+8)a2
6、下列计算是否正确?为什么
(1) (5x+2y)(5x-2y)=(5x)2-(2y)2=25x2-4y2
(2) (-1+3a)(-1-3a)=(-1)2+(3a)2=1+9a2
(3) (-2x-3y)(3y-2x)=(3y)2-(2x)2=9y2-4x2
7、计算:
(1) (3+x)(3-x) (2) (x2-y3)(x2+y3)
(3) (a3b5+c3d4)(c3d4-a3b5) (4) (-a-3ab)(-3ab+a)
8、计算:
(1) (-0.5a-0.2)2 (2) ()2 (3) (am-bn)2 (4) 982
(5) (1-y)2-(1+y)(-1-y) (6) (x-2y)(x+2y)-(x+2y)2 (7) (m+2)2(m-2)2
9、已知 a+b=2,a b=1 求a2+b2、(a-b)2的值
10、先化简,再求值
,其中a=-5
思路点拨:对于这个混合运算,先算乘方,再算除,后算加减,有括号的先算括号里的
11、对下列多项式进行因式分解:
(1)4x3y+4x2y2+xy3; (2)3x3-12xy2
12、把下列各式分解因式:
⑴ ⑵ ⑶
⑷ ⑸
幂的运算
单项式乘以单项式
单项式乘以多项式
多项式乘以多项式
因式分解
提公因式法
公式法
单项式除以单项式
多项式除以单项式
乘法公式
执笔人:仝蒙蒙 审核人:刘淑玲 使用时间:
一、知识结构
二、 例题选讲
1、计算下列各式:
(1) (-2)2·(-2)3 ;(2) a2·a4·a3 ;(3) x5·x·(-x)3 ;
(4) (a+b-c)2·(c-a-b)3(5) 100·10n+1·10n-1 ;(6) (x+2)n-1·(2+x)n+1-(x+2)2n
解题方法:熟记公式是解这类题的前提,当题中幂的底数不同时,必须利用乘法和乘方的意义变形,化成同底数幂;当题目中有加、减、乘混合运算时,应计算同底数幂的乘法,然后再合并同类项.
2、计算下列各式:
(1) [(-2)2]6 ;(2) [(x+y)3]4 ;(3) (a4n)n-1 ;(4) -(y4)2·(y2)3 ;
(5) (-a3)2+(-a2)3-(-a2)·(-a)4 ;(6) x3·x2·x4+(-x4)2+4(-x2)4
3、计算下列各式:
(1) (-3a4)3 ; (2) (a2b3)m ;
(3) [(x+y)(x-y)]5 ; (4) (x m+2·y 2n-1)2 ;
(5) (-0.125)8×225 ;(6) (1990)n·()n+1 ;
4、已知22x+1+4x=48,求x的值.
解题方法:解这种有关指数方程的基本方法是,将左右两边变形为两个幂相等的等式,且左右两边幂的底数相同,再根据两个底数相同的幂相等,其指数必定相等列出方程,解这个方程即可.
三、课堂练习
1、计算:
(1) 3x2y·(-2xy3) (2) (-5a2b3)·(-4b2c)·a2b
2、计算:
(1) (-2a2)·(3ab2-5ab3) (2) (-2x2y)2(-y2+xy+x3)
3、已知x+y=4,x-y=6,求代数式x y(y2+y)-y2(x y+2x)-3x y的值
4、计算:
(1) (3x2-2x-5)(-2x+3) (2) (2x-y)(4x2+2xy+y2)
(3) (3a+2b)2 (4) (x-1)(2x-3)(3x+1)
5、已知(a2+pa+8)与(a2-3a+q)的乘积中不含a3和a2项,求p、q的值.
分析:不含有这个项,即为此项的系数为零,又(a2+pa+8)与(a2-3a+q)的乘积中的a3项是-3a3+pa3=(-3+p)a3, a2项是qa2-3pa2+8a2=(q-3 p+8)a2
6、下列计算是否正确?为什么
(1) (5x+2y)(5x-2y)=(5x)2-(2y)2=25x2-4y2
(2) (-1+3a)(-1-3a)=(-1)2+(3a)2=1+9a2
(3) (-2x-3y)(3y-2x)=(3y)2-(2x)2=9y2-4x2
7、计算:
(1) (3+x)(3-x) (2) (x2-y3)(x2+y3)
(3) (a3b5+c3d4)(c3d4-a3b5) (4) (-a-3ab)(-3ab+a)
8、计算:
(1) (-0.5a-0.2)2 (2) ()2 (3) (am-bn)2 (4) 982
(5) (1-y)2-(1+y)(-1-y) (6) (x-2y)(x+2y)-(x+2y)2 (7) (m+2)2(m-2)2
9、已知 a+b=2,a b=1 求a2+b2、(a-b)2的值
10、先化简,再求值
,其中a=-5
思路点拨:对于这个混合运算,先算乘方,再算除,后算加减,有括号的先算括号里的
11、对下列多项式进行因式分解:
(1)4x3y+4x2y2+xy3; (2)3x3-12xy2
12、把下列各式分解因式:
⑴ ⑵ ⑶
⑷ ⑸
幂的运算
单项式乘以单项式
单项式乘以多项式
多项式乘以多项式
因式分解
提公因式法
公式法
单项式除以单项式
多项式除以单项式
乘法公式
