高二数学必修3统计单元测试题(无答案)
文档属性
| 名称 | 高二数学必修3统计单元测试题(无答案) |

|
|
| 格式 | rar | ||
| 文件大小 | 71.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-10 00:00:00 | ||
图片预览


文档简介
高二数学必修3统计单元练习
班级 姓名 学号
参考:最小二乘法求线性回归方程系数公式.
1、某一市场进行调查,规定在大都会商场门口随机抽一个人进行询问调查,直到调查到事先规定的调查人数为止,这种抽样方式是 ( )
A、系统抽样 B、分层抽样 C、简单随机抽样 D、非以上三种抽样方法
2、为了解所加工的一批零件的长度,抽测其中200个零件的长度,在此问题中,200个零件的长度是 ( )
A、总体 B、个体 C、总体的一个样本 D、样本容量
3、在120个零件中,一级品24个,二级品36个,三级品60个,从中抽取容量为20的样本则每个样本被抽到的概率( )
A、 B、 C、 D、不确定
4、在抽查某产品尺寸的过程中,将其尺寸分成若干组,[a,b]是其中一组,抽查出的个体数在该组上的频率为m,该组上的直方图的高是h,则, ba等于 ( )
A、hm B、 C、 D、 与m,h无关
5、变量y与x之间的回归方程( )
A、表示y与x之间的函数关系 B、表示y和x之间的不确定关系
C、反映y和x之间真实关系的形式
D、反映y与x之间的真实关系达到最大限度的吻合
6、线性回归方程=bx+a必过点 ( )
A、(0,0) B、(,0) C、(0,) D、(,)
7、已知甲、乙两名同学在五次数学测验中的得分如下:
甲:85,91,90,89,95;乙:95,80,98,82,95.
则甲、乙两名同学数学学习成绩 ( )
A、甲比乙稳定 B、甲、乙稳定程度相同
C、乙比甲稳定 D、无法确定
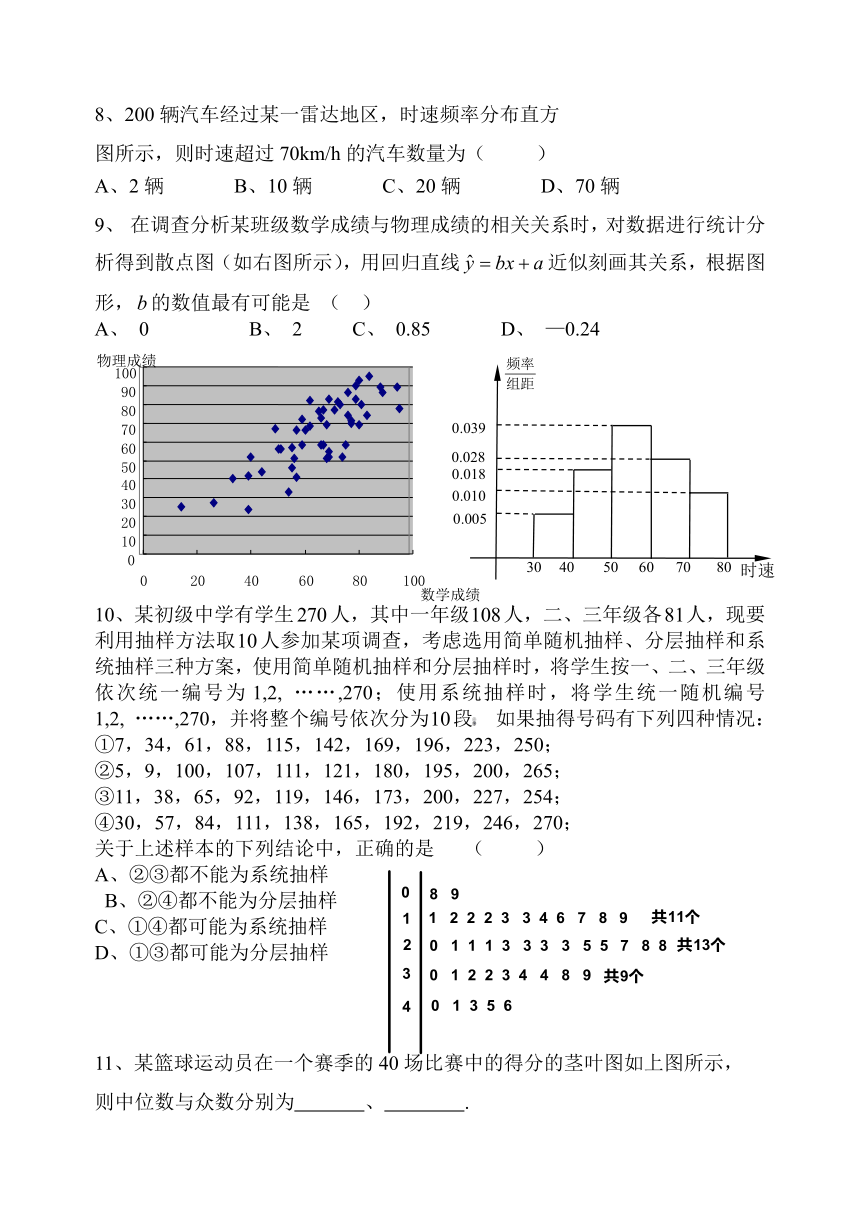
8、200辆汽车经过某一雷达地区,时速频率分布直方
图所示,则时速超过70km/h的汽车数量为( )
A、2辆 B、10辆 C、20辆 D、70辆
9、 在调查分析某班级数学成绩与物理成绩的相关关系时,对数据进行统计分析得到散点图(如右图所示),用回归直线近似刻画其关系,根据图形,的数值最有可能是 ( )
A、 0 B、 2 C、 0.85 D、 —0.24
10、某初级中学有学生人,其中一年级人,二、三年级各人,现要利用抽样方法取人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为1,2, ……,270;使用系统抽样时,将学生统一随机编号1,2, ……,270,并将整个编号依次分为段 如果抽得号码有下列四种情况:
①7,34,61,88,115,142,169,196,223,250;
②5,9,100,107,111,121,180,195,200,265;
③11,38,65,92,119,146,173,200,227,254;
④30,57,84,111,138,165,192,219,246,270;
关于上述样本的下列结论中,正确的是 ( )
A、②③都不能为系统抽样
B、②④都不能为分层抽样
C、①④都可能为系统抽样
D、①③都可能为分层抽样
11、某篮球运动员在一个赛季的40场比赛中的得分的茎叶图如上图所示,
则中位数与众数分别为 、 .
12、从2005个编号中抽取20个号码作为样本,若采用系统抽样的方法,则抽样的间隔为 ___
13、某校共有学生2000名,各年级男、女生人数
一年级
二年级
三年级
女生
373
x
y
男生
377
370
z
如右下表.已知在全校学生中随机抽取1名,抽到二年级女生的可能性是0.19.现用分层抽样的方法在全校抽取64名学生,则应在三年级抽取的学生人数为 .
14、某班40人随机平均分成两组,两组学生一次考试的成绩情况如下表:
平均值
标准差
第一组
90
第二组
80
4
则全班学生的平均成绩是 ,标准差是 .
15、下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(吨)与相应的生产能耗 (吨标准煤)的几组对照数据
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出关于的线性回归方程;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:)
解:
15、在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,将数据分组如下表:
(1)完成频率分布表,并在给定的坐标系中画出频率分布直方图和频率分布折线图;
(2)估计纤度落在中的概率是多少?纤度小于的概率是多少?
(3)统计方法中,同一组数据常用该组区间的中点值(例如区间的中点值是)作为代表.据此,估计纤度的众数,平均值,中位数.(要求:结果精确到0.01)
解:(1)
分组
频数
频率
0.30
0.10
合计
数学单元练习2-统计
一、填空题
1.在统计里,常用的抽样方法有:
2.管理人员从一池塘内捞出30条鱼,做上标记后放回池塘。10天后,又从池塘内捞出50条鱼,其中有标记的有2条。根据以上数据可以估计该池塘内共有 条鱼。
3.一个总体中有200个个体,随机编号为00,01,02,03,…,199.依编号顺序平均分成20个小组,组号依次为1,2,3,…,20,现用系统抽样方法抽取一个容量为20的样本,规定如果在第1组随机抽取的号码为m,那么在第k组抽取的号码的个位数字与m+k的个位数字相同.若m=6,则在第7组中抽取的号码是 _______ 。
4.如图是年元旦晚会举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的众数和中位数分别为____,____.。
5.为了解某地高一年级男生的身高情况,从其中的一个学校选取容量为60的样本
(60名男生的身高,单位:cm),分组情况如下:
分组
151.5~158.5
158.5~165.5
165.5~172.5
172.5~179.5
频数
6
2l
频率
0.1
则表中的 , 。
6. 已知样本的平均数是,标准差是,则的值为______ 。
7. 统计某校1000名学生的数学会考成绩,得到样
本频率分布直方图如右图示,规定不低于60分为
及格,不低于80分为优秀,则及格人数是 ;
优秀率为 。
.
二 解答题
8. 某电脑公司有6名产品推销员,其工作年限与年推销金额数据如下表:
推销员编号
1
2
3
4
5
工作年限/年
3
5
6
7
9
推销金额/万元
2
3
3
4
5
(Ⅰ) 求年推销金额关于工作年限的线性回归方程
(Ⅱ)若第6名推销员的工作年限为11年,试估计他的年推销金额.
9. 某校从参加高一年级期末考试的学生中抽出60名
学生,将其成绩(均为整数)分成六段,…后画出
如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求第四小组的频率,并补全这个频率分布直方图;
(Ⅱ)估计这次考试的及格率(60分及以上为及格)和平均分;
10 已知一组数据的方差是2,且,求这组数据的平均数。
班级 姓名 学号
参考:最小二乘法求线性回归方程系数公式.
1、某一市场进行调查,规定在大都会商场门口随机抽一个人进行询问调查,直到调查到事先规定的调查人数为止,这种抽样方式是 ( )
A、系统抽样 B、分层抽样 C、简单随机抽样 D、非以上三种抽样方法
2、为了解所加工的一批零件的长度,抽测其中200个零件的长度,在此问题中,200个零件的长度是 ( )
A、总体 B、个体 C、总体的一个样本 D、样本容量
3、在120个零件中,一级品24个,二级品36个,三级品60个,从中抽取容量为20的样本则每个样本被抽到的概率( )
A、 B、 C、 D、不确定
4、在抽查某产品尺寸的过程中,将其尺寸分成若干组,[a,b]是其中一组,抽查出的个体数在该组上的频率为m,该组上的直方图的高是h,则, ba等于 ( )
A、hm B、 C、 D、 与m,h无关
5、变量y与x之间的回归方程( )
A、表示y与x之间的函数关系 B、表示y和x之间的不确定关系
C、反映y和x之间真实关系的形式
D、反映y与x之间的真实关系达到最大限度的吻合
6、线性回归方程=bx+a必过点 ( )
A、(0,0) B、(,0) C、(0,) D、(,)
7、已知甲、乙两名同学在五次数学测验中的得分如下:
甲:85,91,90,89,95;乙:95,80,98,82,95.
则甲、乙两名同学数学学习成绩 ( )
A、甲比乙稳定 B、甲、乙稳定程度相同
C、乙比甲稳定 D、无法确定
8、200辆汽车经过某一雷达地区,时速频率分布直方
图所示,则时速超过70km/h的汽车数量为( )
A、2辆 B、10辆 C、20辆 D、70辆
9、 在调查分析某班级数学成绩与物理成绩的相关关系时,对数据进行统计分析得到散点图(如右图所示),用回归直线近似刻画其关系,根据图形,的数值最有可能是 ( )
A、 0 B、 2 C、 0.85 D、 —0.24
10、某初级中学有学生人,其中一年级人,二、三年级各人,现要利用抽样方法取人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为1,2, ……,270;使用系统抽样时,将学生统一随机编号1,2, ……,270,并将整个编号依次分为段 如果抽得号码有下列四种情况:
①7,34,61,88,115,142,169,196,223,250;
②5,9,100,107,111,121,180,195,200,265;
③11,38,65,92,119,146,173,200,227,254;
④30,57,84,111,138,165,192,219,246,270;
关于上述样本的下列结论中,正确的是 ( )
A、②③都不能为系统抽样
B、②④都不能为分层抽样
C、①④都可能为系统抽样
D、①③都可能为分层抽样
11、某篮球运动员在一个赛季的40场比赛中的得分的茎叶图如上图所示,
则中位数与众数分别为 、 .
12、从2005个编号中抽取20个号码作为样本,若采用系统抽样的方法,则抽样的间隔为 ___
13、某校共有学生2000名,各年级男、女生人数
一年级
二年级
三年级
女生
373
x
y
男生
377
370
z
如右下表.已知在全校学生中随机抽取1名,抽到二年级女生的可能性是0.19.现用分层抽样的方法在全校抽取64名学生,则应在三年级抽取的学生人数为 .
14、某班40人随机平均分成两组,两组学生一次考试的成绩情况如下表:
平均值
标准差
第一组
90
第二组
80
4
则全班学生的平均成绩是 ,标准差是 .
15、下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(吨)与相应的生产能耗 (吨标准煤)的几组对照数据
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出关于的线性回归方程;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:)
解:
15、在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,将数据分组如下表:
(1)完成频率分布表,并在给定的坐标系中画出频率分布直方图和频率分布折线图;
(2)估计纤度落在中的概率是多少?纤度小于的概率是多少?
(3)统计方法中,同一组数据常用该组区间的中点值(例如区间的中点值是)作为代表.据此,估计纤度的众数,平均值,中位数.(要求:结果精确到0.01)
解:(1)
分组
频数
频率
0.30
0.10
合计
数学单元练习2-统计
一、填空题
1.在统计里,常用的抽样方法有:
2.管理人员从一池塘内捞出30条鱼,做上标记后放回池塘。10天后,又从池塘内捞出50条鱼,其中有标记的有2条。根据以上数据可以估计该池塘内共有 条鱼。
3.一个总体中有200个个体,随机编号为00,01,02,03,…,199.依编号顺序平均分成20个小组,组号依次为1,2,3,…,20,现用系统抽样方法抽取一个容量为20的样本,规定如果在第1组随机抽取的号码为m,那么在第k组抽取的号码的个位数字与m+k的个位数字相同.若m=6,则在第7组中抽取的号码是 _______ 。
4.如图是年元旦晚会举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的众数和中位数分别为____,____.。
5.为了解某地高一年级男生的身高情况,从其中的一个学校选取容量为60的样本
(60名男生的身高,单位:cm),分组情况如下:
分组
151.5~158.5
158.5~165.5
165.5~172.5
172.5~179.5
频数
6
2l
频率
0.1
则表中的 , 。
6. 已知样本的平均数是,标准差是,则的值为______ 。
7. 统计某校1000名学生的数学会考成绩,得到样
本频率分布直方图如右图示,规定不低于60分为
及格,不低于80分为优秀,则及格人数是 ;
优秀率为 。
.
二 解答题
8. 某电脑公司有6名产品推销员,其工作年限与年推销金额数据如下表:
推销员编号
1
2
3
4
5
工作年限/年
3
5
6
7
9
推销金额/万元
2
3
3
4
5
(Ⅰ) 求年推销金额关于工作年限的线性回归方程
(Ⅱ)若第6名推销员的工作年限为11年,试估计他的年推销金额.
9. 某校从参加高一年级期末考试的学生中抽出60名
学生,将其成绩(均为整数)分成六段,…后画出
如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求第四小组的频率,并补全这个频率分布直方图;
(Ⅱ)估计这次考试的及格率(60分及以上为及格)和平均分;
10 已知一组数据的方差是2,且,求这组数据的平均数。
