直线和圆的位置关系
图片预览







文档简介
课件21张PPT。海平面 直线与圆的位置关系直线和圆的位置有
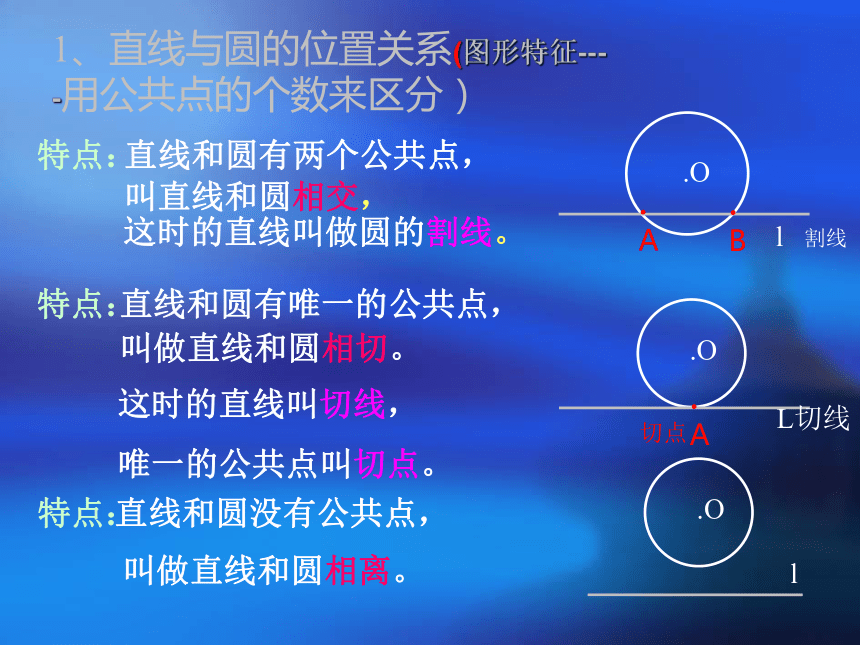
何关系???lll直线与圆的位置关系.Ol特点:.O叫做直线和圆相离。直线和圆没有公共点,L切线特点:直线和圆有唯一的公共点,叫做直线和圆相切。这时的直线叫切线,
唯一的公共点叫切点。.Ol特点:直线和圆有两个公共点,叫直线和圆相交,这时的直线叫做圆的割线。1、直线与圆的位置关系(图形特征----用公共点的个数来区分).A.A.B切点割线小问题:如何根据基本概念来判断直线与圆的位置关系?根据直线与圆的公共点的个数来判断练习1 :快速判断下列各图中直线与圆的位置关系ll.O2lL.练习2 1、直线与圆最多有两个公共点 。… ( ) √×?判断3 、若A是⊙O上一点, 则直线AB与⊙O相切 。( ).A.O2、若直线与圆相交,则直线上的点都在圆内。( ) 4 、若C为⊙O外的一点,则过点C的直线CD与
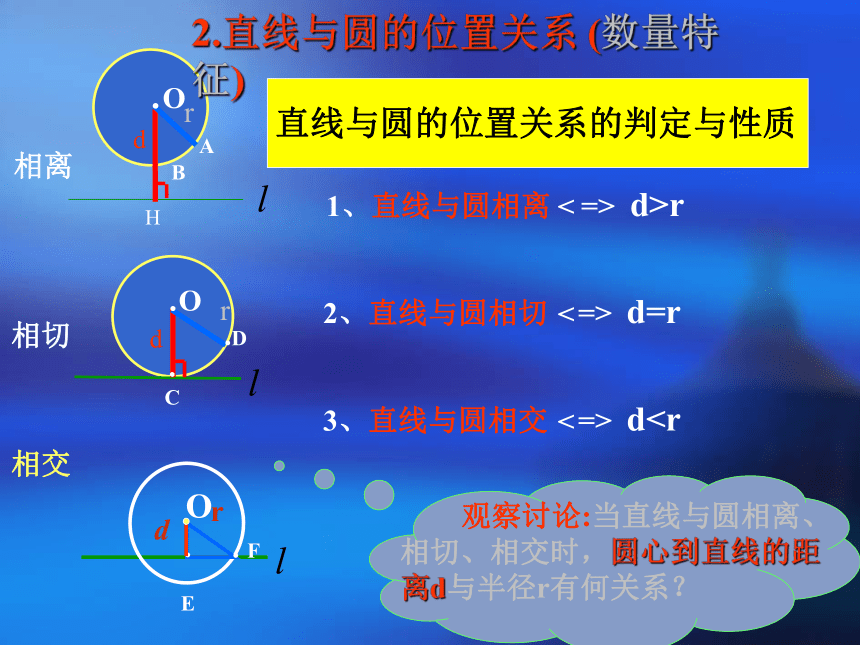
⊙O 相交或相离。………( )××.C新的问题:除了用公共点的个数来区分直线与圆的位置关系外,能否像点和圆的位置关系一样用数量关系的方法来判断直线与圆的位置关系?<
<
<
dr相离Adr相切H1、直线与圆相离 => d>r2、直线与圆相切 => d=r3、直线与圆相交 => dC.OB直线与圆的位置关系的判定与性质.
E. FO总结:判定直线 与圆的位置关系的方法有____种:(1)根据定义,由________________
的个数来判断;(2)根据性质,由_________________ 的关系来判断。在实际应用中,常采用第二种方法判定。两直线 与圆的公共点圆心到直线的距离d与半径r
圆的直径是13cm,如果直线与圆心的距离分别是(1)4.5cm ; (2) 6.5cm ; (3) 8cm,
那么直线与圆分别是什么位置关系? 有几个公共点?有两个公共点;有一个公共点;没有公共点.例题1:填空:1、已知⊙O的半径为5cm,点O到直线a的距离
为3cm,则⊙O与直线a的位置关系是_____;
直线a与⊙O的公共点个数是____.动动脑筋相交 相切两个3、已知⊙O的直径为10cm,点O到直线a的距离
为7cm,则⊙O与直线a的位置关系是 ___ _;
直线a与⊙O的公共点个数是____。零相离一个小结:利用圆心到直线的距离与半径的大小关
系来识别直线与圆的位置关系2、已知⊙O的直径是11cm,点O到直线a的距离
是5.5cm,则⊙O与直线a的位置关系是 ___ _;
直线a与⊙O的公共点个数是____.4、直线m上一点A到圆心O的距离等于⊙O的半径,
则直线m与⊙O的位置关系是 。相切 或相交思考:圆心A到X轴、
Y轴的距离各是多少?例题1:O 已知⊙A的直径为6,点A的坐标为(-3,-4),则⊙A与X轴的位置关系是_____,⊙A与Y轴的位置关系是______。BC43相离相切.A例题2:分析在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆
与AB有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm (3)r=3cm。BCAD4532.4cm即圆心C到AB的距离d=2.4cm。(1)当r=2cm时, ∵d>r,
∴⊙C与AB相离。(2)当r=2.4cm时,∵d=r,
∴⊙C与AB相切。(3)当r=3cm时, ∵d<r,
∴⊙C与AB相交。解:过C作CD⊥AB,垂足为D。在Rt△ABC中,AB= ==5(cm)根据三角形面积公式有CD·AB=AC·BC∴CD= =2222=2.4(cm)。ABCAD453d=2.4例: Rt△ABC,∠C=90°AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm
(3)r=3cm。 1、如图,已知∠AOB=30°,M为OB上一点,且OM=5cm,以M为圆心、以r为半径的圆与直线OA有怎样的位置关系?为什么 ? ⑴ r =2cm; ⑵ r =4cm; ⑶ r =2.5cm。解:过点M作MC⊥OA于C ,
∵ ∠AOB=30°, OM=5cm, ∴ MC=2.5cm ⑴ ∵ d=MC=2.5, r=2 即d >r
∴ ⊙O与OA相离;
⑵ ∵ d=MC=2.5, r=4 即d < r
∴ ⊙O与OA相交;
⑶ ∵ d=MC=2.5, r=2.5 即d= r
∴ ⊙O与OA相切.课堂练习. 随堂检测
1.⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l
与⊙O没有公共点,则d为( ):
A.d >3 B.d<3 C.d ≤3 D.d =3
2.圆心O到直线的距离等于⊙O的半径,则直线
和⊙O的位置 关系是( ):
A.相离 B.相交 C.相切 D.相切或相交
3.判断:若直线和圆相切,则该直线和圆一定有一个公共点.( )
4.等边三角形ABC的边长为2,则以A为圆心,半径为1.73的圆
与直线BC的位置关系是 ,以A为圆心,
为半径的圆与直线BC相切.AC√相离小结:0d>r1d=r切点切线2d2、思考题:(1)当 r 满足______时,⊙C与直线AB相离。1.在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,
以C为圆心,r为半径作圆。 再见
何关系???lll直线与圆的位置关系.Ol特点:.O叫做直线和圆相离。直线和圆没有公共点,L切线特点:直线和圆有唯一的公共点,叫做直线和圆相切。这时的直线叫切线,
唯一的公共点叫切点。.Ol特点:直线和圆有两个公共点,叫直线和圆相交,这时的直线叫做圆的割线。1、直线与圆的位置关系(图形特征----用公共点的个数来区分).A.A.B切点割线小问题:如何根据基本概念来判断直线与圆的位置关系?根据直线与圆的公共点的个数来判断练习1 :快速判断下列各图中直线与圆的位置关系ll.O2lL.练习2 1、直线与圆最多有两个公共点 。… ( ) √×?判断3 、若A是⊙O上一点, 则直线AB与⊙O相切 。( ).A.O2、若直线与圆相交,则直线上的点都在圆内。( ) 4 、若C为⊙O外的一点,则过点C的直线CD与
⊙O 相交或相离。………( )××.C新的问题:除了用公共点的个数来区分直线与圆的位置关系外,能否像点和圆的位置关系一样用数量关系的方法来判断直线与圆的位置关系?<
<
<
dr相离Adr相切H1、直线与圆相离 => d>r2、直线与圆相切 => d=r3、直线与圆相交 => d
E. FO总结:判定直线 与圆的位置关系的方法有____种:(1)根据定义,由________________
的个数来判断;(2)根据性质,由_________________ 的关系来判断。在实际应用中,常采用第二种方法判定。两直线 与圆的公共点圆心到直线的距离d与半径r
圆的直径是13cm,如果直线与圆心的距离分别是(1)4.5cm ; (2) 6.5cm ; (3) 8cm,
那么直线与圆分别是什么位置关系? 有几个公共点?有两个公共点;有一个公共点;没有公共点.例题1:填空:1、已知⊙O的半径为5cm,点O到直线a的距离
为3cm,则⊙O与直线a的位置关系是_____;
直线a与⊙O的公共点个数是____.动动脑筋相交 相切两个3、已知⊙O的直径为10cm,点O到直线a的距离
为7cm,则⊙O与直线a的位置关系是 ___ _;
直线a与⊙O的公共点个数是____。零相离一个小结:利用圆心到直线的距离与半径的大小关
系来识别直线与圆的位置关系2、已知⊙O的直径是11cm,点O到直线a的距离
是5.5cm,则⊙O与直线a的位置关系是 ___ _;
直线a与⊙O的公共点个数是____.4、直线m上一点A到圆心O的距离等于⊙O的半径,
则直线m与⊙O的位置关系是 。相切 或相交思考:圆心A到X轴、
Y轴的距离各是多少?例题1:O 已知⊙A的直径为6,点A的坐标为(-3,-4),则⊙A与X轴的位置关系是_____,⊙A与Y轴的位置关系是______。BC43相离相切.A例题2:分析在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,以C为圆心,r为半径的圆
与AB有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm (3)r=3cm。BCAD4532.4cm即圆心C到AB的距离d=2.4cm。(1)当r=2cm时, ∵d>r,
∴⊙C与AB相离。(2)当r=2.4cm时,∵d=r,
∴⊙C与AB相切。(3)当r=3cm时, ∵d<r,
∴⊙C与AB相交。解:过C作CD⊥AB,垂足为D。在Rt△ABC中,AB= ==5(cm)根据三角形面积公式有CD·AB=AC·BC∴CD= =2222=2.4(cm)。ABCAD453d=2.4例: Rt△ABC,∠C=90°AC=3cm,BC=4cm,以C为圆心,r为半径的圆与AB有怎样的位置关系?为什么?
(1)r=2cm;(2)r=2.4cm
(3)r=3cm。 1、如图,已知∠AOB=30°,M为OB上一点,且OM=5cm,以M为圆心、以r为半径的圆与直线OA有怎样的位置关系?为什么 ? ⑴ r =2cm; ⑵ r =4cm; ⑶ r =2.5cm。解:过点M作MC⊥OA于C ,
∵ ∠AOB=30°, OM=5cm, ∴ MC=2.5cm ⑴ ∵ d=MC=2.5, r=2 即d >r
∴ ⊙O与OA相离;
⑵ ∵ d=MC=2.5, r=4 即d < r
∴ ⊙O与OA相交;
⑶ ∵ d=MC=2.5, r=2.5 即d= r
∴ ⊙O与OA相切.课堂练习. 随堂检测
1.⊙O的半径为3 ,圆心O到直线l的距离为d,若直线l
与⊙O没有公共点,则d为( ):
A.d >3 B.d<3 C.d ≤3 D.d =3
2.圆心O到直线的距离等于⊙O的半径,则直线
和⊙O的位置 关系是( ):
A.相离 B.相交 C.相切 D.相切或相交
3.判断:若直线和圆相切,则该直线和圆一定有一个公共点.( )
4.等边三角形ABC的边长为2,则以A为圆心,半径为1.73的圆
与直线BC的位置关系是 ,以A为圆心,
为半径的圆与直线BC相切.AC√相离小结:0d>r1d=r切点切线2d
以C为圆心,r为半径作圆。 再见
同课章节目录
