24.2.2切线的判定
图片预览





文档简介
课件28张PPT。切 线 的 判 定24.2.2直线与圆的位置关系 只要你认真听完今天的课你就会明白!问题 1 当你在下雨天快速转动雨伞时水飞出的方向是什么方向?
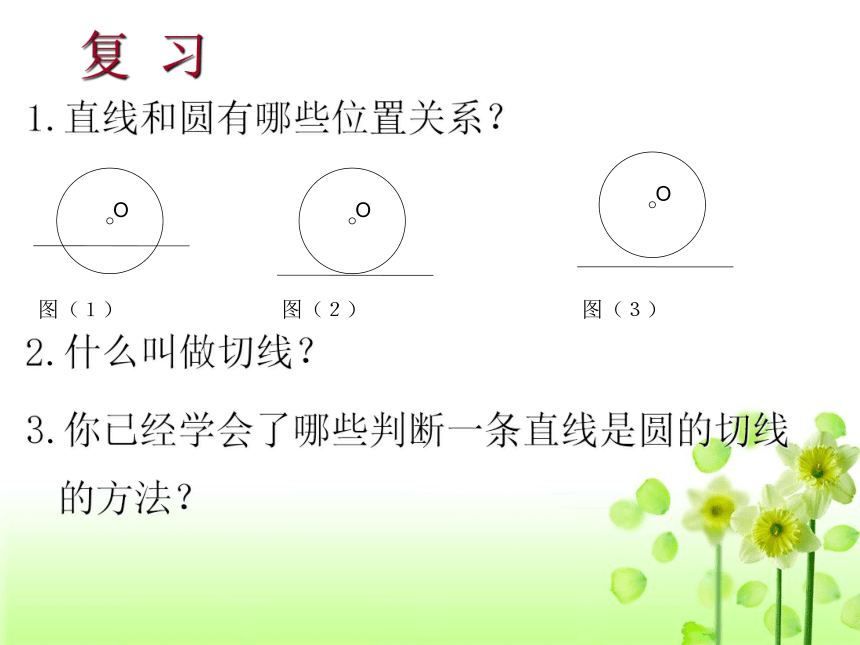
2 砂轮打磨工件飞出火星的方向是什么方向?1.直线和圆有哪些位置关系?
2.什么叫做切线?
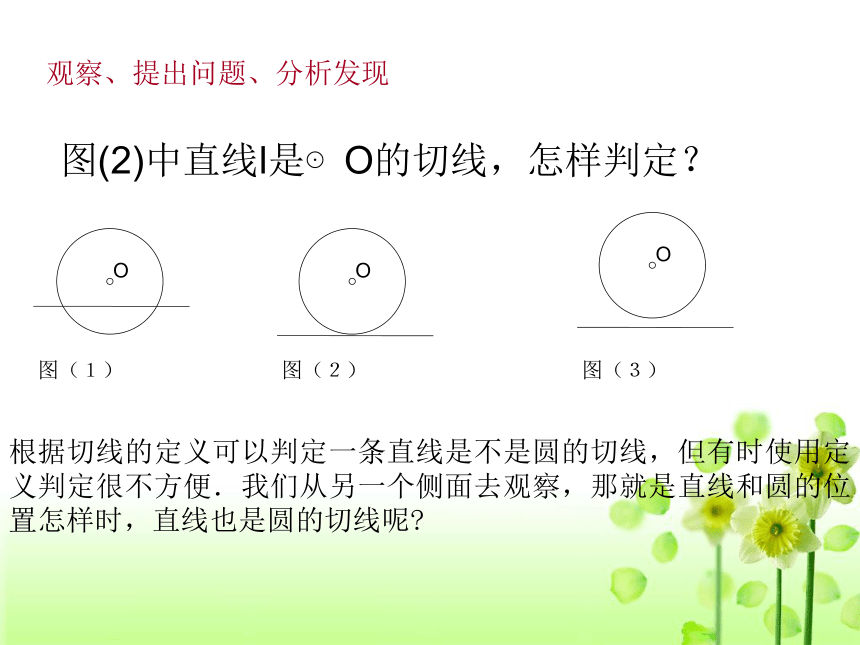
3.你已经学会了哪些判断一条直线是圆的切线的方法?复 习观察、提出问题、分析发现 根据切线的定义可以判定一条直线是不是圆的切线,但有时使用定义判定很不方便.我们从另一个侧面去观察,那就是直线和圆的位置怎样时,直线也是圆的切线呢?
图(2)中直线l是⊙O的切线,怎样判定? 请在⊙O上任意取一点A,连接OA。过点A作直线 l⊥OA。思考一下问题:
1. 圆心O到直线l的距离和圆的半径有什么数量关系?
2. 二者位置有什么关系?为什么?
3. 由此你发现了什么?l发现:(1)直线 l 经过半径OA的外端点A;
(2)直线l垂直于半径0A.
则:直线l与⊙O相切这样我们就得到了从
位置上来判定直线是圆的切线的方法——切线的判定定理.
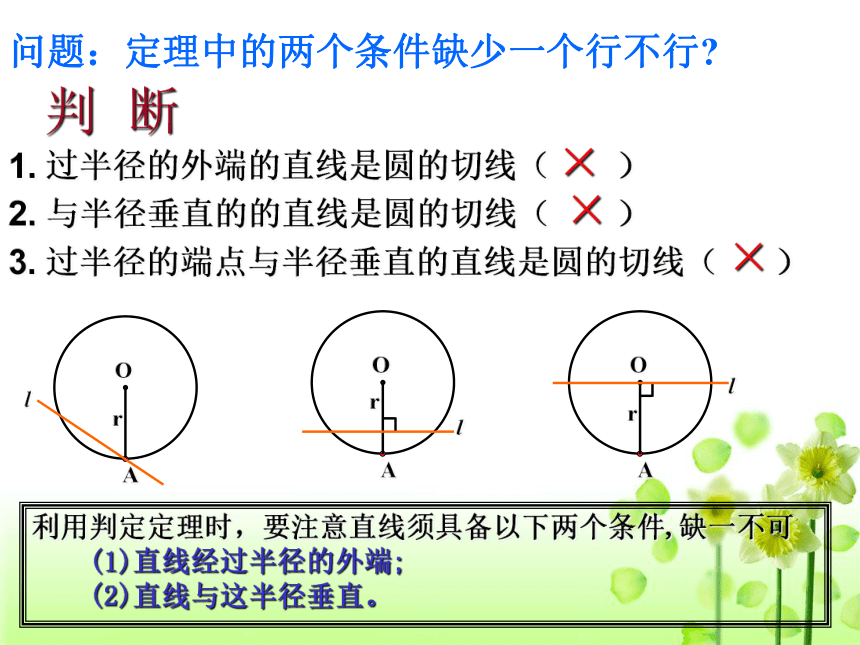
直线与圆相切的判定定理: 经过半径的外端并且垂直这条半径的直线是圆的切线。 对定理的理解:切线需满足两条: ①经过半径外端;②垂直于这条半径. 判 断1. 过半径的外端的直线是圆的切线( )
2. 与半径垂直的的直线是圆的切线( )
3. 过半径的端点与半径垂直的直线是圆的切线( )×××利用判定定理时,要注意直线须具备以下两个条件,缺一不可
(1)直线经过半径的外端;
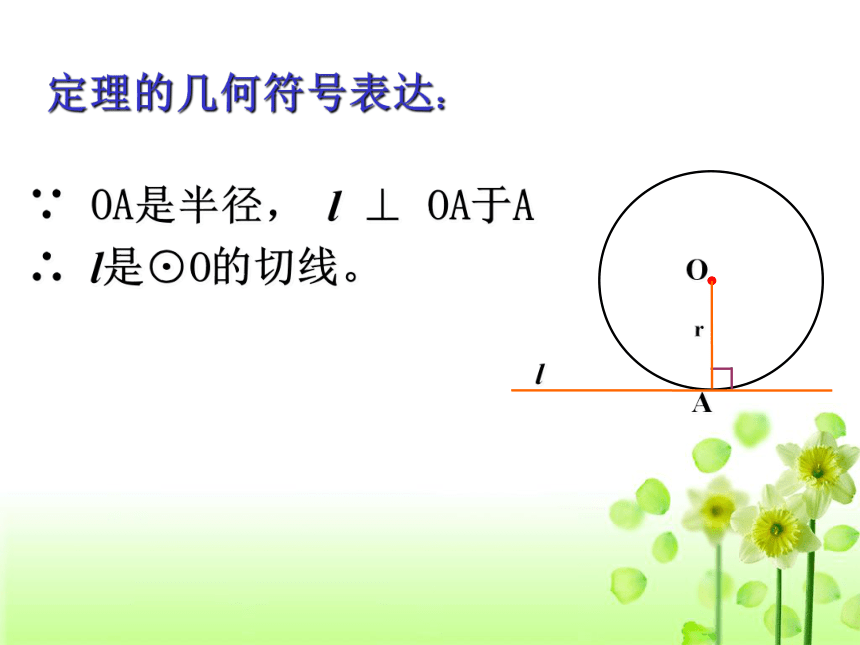
(2)直线与这半径垂直。问题:定理中的两个条件缺少一个行不行? Orl A∵ OA是半径, l ⊥ OA于A
∴ l是⊙O的切线。定理的几何符号表达:
切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即
经过半径的外端并且垂直这条半径的直线是圆的切线
判定直线与圆相切有哪些方法? 〖例1〗已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。OBAC分析:由于AB过⊙O上的点C,所以连接OC,只要证明
AB⊥OC即可。 证明:连结OC(如图)。
∵ ⊿OAB中, OA=OB , CA=CB,
∴ AB⊥OC。
∵ OC是⊙O的半径
∴ AB是⊙O的切线。〖例2〗已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为
半径作⊙O。
求证:⊙O与AC相切。OABCD证明:过O作OE⊥AC于E。
∵ AO平分∠BAC,OD⊥AB
∴ OE=OD
即圆心O到AC的距离 d = r
∴ AC是⊙O切线。小 结例1与例2的证法有何不同?
(1)如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直。简记为:连半径,证垂直。
(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段为辅助线,再证垂线段长等于半径长。简记为:作垂直,证半径。.如图, △ABC中,AB=AC,AD⊥BC于D,DE ⊥AC于E,以D为圆心,DE为半径作⊙D.
求证:AB是⊙D的切线.FECDBA例1的变化:如图,已知:OA=OB=5, AB=8,以O为圆心,以3为半径的圆与直线AB 相切吗?为什么? OAB 例3 已知:如图A是⊙O外一点,AO的延长线交⊙O于点C,点B在圆上,且AB=BC,∠A=30O。求证:直线AB是⊙O的切线。变.如图,AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在⊙O上, ∠CAB=30°,求证:DC是⊙O的切线.
例4.以Rt△ABC的直角边BC为直径作半圆O,交斜边于D,OE∥AC交AB于E,求证:DE是⊙O的切线.例5.如图,在梯形ABCD中,AD ∥BC,AB=DC,以AB为直径的⊙O交BC于点E,过E点作DC的垂线EF,F为垂足,求证:EF是⊙O的切线变:把”梯形ABCD”改为”等腰三角形ABC,AB=AC”1 判断下列命题是否正确.
(1)经过半径外端的直线是圆的切线.
(2)垂直于半径的直线是圆的切线.
(3)过直径的外端并且垂直于这条直径的直线是圆的切线.
(4)和圆有一个公共点的直线是圆的切线.
(5)以等腰三角形的顶点为圆心,底边上的高为半径的圆与底边相切.
练习2.如图,AB是⊙O的直径, ∠ABT=45°,AT=AB,求证:AT是⊙O的切线.
拓 如图,台风中心P(100,200)沿北偏东30O方向移动,受台风影响区域的半径为200km,那么下列城市A(200,380),B(600,480),C(550,300),D(370,540)中,哪些城市要做抗台风准备?如图,台风中心P(100,200)沿北偏东27O方向移动,受台风影响区域的半径为200km,那么下列城市A(200,380),B(600,480),C(550,300),D(370,540)中,哪些城市要做抗台风准备?P小结本课1、切线的判定方法;
2、切线的作法;
3、常见辅助线;
4、综合应用。 1、知识:切线的判定定理.着重分析了定理成立的条件,在应用定理时,注重两个条件缺一不可.
2、方法:判定一条直线是圆的切线的三种方法:
(1) 根据切线定义判定.即与圆有唯一公共点的直线是圆的切线.
(2)根据圆心到直线的距离来判定,即与圆心的距离等于圆的半径的直线是圆的切线.
(3)根据切线的判定定理来判定.
其中(2)和(3)本质相同,只是表达形式不同.解题时,灵活选用其中之一.
下雨天转动雨伞时飞出的水,以及在砂轮上打磨工件飞 出的火星,均沿着圆的切线的方向飞出. 1 当你在下雨天快速转动雨伞时水飞出的方向是什么方向?
2 砂轮打磨工件飞出火星的方向是什么方向?现在你知道:Class over
88!直线和圆相交d rd r 直线和圆相切直线和圆相离d r●O相交相切 相离┐dd┐d┐<=>知识回顾
2 砂轮打磨工件飞出火星的方向是什么方向?1.直线和圆有哪些位置关系?
2.什么叫做切线?
3.你已经学会了哪些判断一条直线是圆的切线的方法?复 习观察、提出问题、分析发现 根据切线的定义可以判定一条直线是不是圆的切线,但有时使用定义判定很不方便.我们从另一个侧面去观察,那就是直线和圆的位置怎样时,直线也是圆的切线呢?
图(2)中直线l是⊙O的切线,怎样判定? 请在⊙O上任意取一点A,连接OA。过点A作直线 l⊥OA。思考一下问题:
1. 圆心O到直线l的距离和圆的半径有什么数量关系?
2. 二者位置有什么关系?为什么?
3. 由此你发现了什么?l发现:(1)直线 l 经过半径OA的外端点A;
(2)直线l垂直于半径0A.
则:直线l与⊙O相切这样我们就得到了从
位置上来判定直线是圆的切线的方法——切线的判定定理.
直线与圆相切的判定定理: 经过半径的外端并且垂直这条半径的直线是圆的切线。 对定理的理解:切线需满足两条: ①经过半径外端;②垂直于这条半径. 判 断1. 过半径的外端的直线是圆的切线( )
2. 与半径垂直的的直线是圆的切线( )
3. 过半径的端点与半径垂直的直线是圆的切线( )×××利用判定定理时,要注意直线须具备以下两个条件,缺一不可
(1)直线经过半径的外端;
(2)直线与这半径垂直。问题:定理中的两个条件缺少一个行不行? Orl A∵ OA是半径, l ⊥ OA于A
∴ l是⊙O的切线。定理的几何符号表达:
切线的判定方法有三种:
①直线与圆有唯一公共点;
②直线到圆心的距离等于该圆的半径;
③切线的判定定理.即
经过半径的外端并且垂直这条半径的直线是圆的切线
判定直线与圆相切有哪些方法? 〖例1〗已知:直线AB经过⊙O上的点C,并且OA=OB,CA=CB。
求证:直线AB是⊙O的切线。OBAC分析:由于AB过⊙O上的点C,所以连接OC,只要证明
AB⊥OC即可。 证明:连结OC(如图)。
∵ ⊿OAB中, OA=OB , CA=CB,
∴ AB⊥OC。
∵ OC是⊙O的半径
∴ AB是⊙O的切线。〖例2〗已知:O为∠BAC平分线上一点,OD⊥AB于D,以O为圆心,OD为
半径作⊙O。
求证:⊙O与AC相切。OABCD证明:过O作OE⊥AC于E。
∵ AO平分∠BAC,OD⊥AB
∴ OE=OD
即圆心O到AC的距离 d = r
∴ AC是⊙O切线。小 结例1与例2的证法有何不同?
(1)如果已知直线经过圆上一点,则连结这点和圆心,得到辅助半径,再证所作半径与这直线垂直。简记为:连半径,证垂直。
(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段为辅助线,再证垂线段长等于半径长。简记为:作垂直,证半径。.如图, △ABC中,AB=AC,AD⊥BC于D,DE ⊥AC于E,以D为圆心,DE为半径作⊙D.
求证:AB是⊙D的切线.FECDBA例1的变化:如图,已知:OA=OB=5, AB=8,以O为圆心,以3为半径的圆与直线AB 相切吗?为什么? OAB 例3 已知:如图A是⊙O外一点,AO的延长线交⊙O于点C,点B在圆上,且AB=BC,∠A=30O。求证:直线AB是⊙O的切线。变.如图,AB是⊙O的直径,点D在AB的延长线上,BD=OB,点C在⊙O上, ∠CAB=30°,求证:DC是⊙O的切线.
例4.以Rt△ABC的直角边BC为直径作半圆O,交斜边于D,OE∥AC交AB于E,求证:DE是⊙O的切线.例5.如图,在梯形ABCD中,AD ∥BC,AB=DC,以AB为直径的⊙O交BC于点E,过E点作DC的垂线EF,F为垂足,求证:EF是⊙O的切线变:把”梯形ABCD”改为”等腰三角形ABC,AB=AC”1 判断下列命题是否正确.
(1)经过半径外端的直线是圆的切线.
(2)垂直于半径的直线是圆的切线.
(3)过直径的外端并且垂直于这条直径的直线是圆的切线.
(4)和圆有一个公共点的直线是圆的切线.
(5)以等腰三角形的顶点为圆心,底边上的高为半径的圆与底边相切.
练习2.如图,AB是⊙O的直径, ∠ABT=45°,AT=AB,求证:AT是⊙O的切线.
拓 如图,台风中心P(100,200)沿北偏东30O方向移动,受台风影响区域的半径为200km,那么下列城市A(200,380),B(600,480),C(550,300),D(370,540)中,哪些城市要做抗台风准备?如图,台风中心P(100,200)沿北偏东27O方向移动,受台风影响区域的半径为200km,那么下列城市A(200,380),B(600,480),C(550,300),D(370,540)中,哪些城市要做抗台风准备?P小结本课1、切线的判定方法;
2、切线的作法;
3、常见辅助线;
4、综合应用。 1、知识:切线的判定定理.着重分析了定理成立的条件,在应用定理时,注重两个条件缺一不可.
2、方法:判定一条直线是圆的切线的三种方法:
(1) 根据切线定义判定.即与圆有唯一公共点的直线是圆的切线.
(2)根据圆心到直线的距离来判定,即与圆心的距离等于圆的半径的直线是圆的切线.
(3)根据切线的判定定理来判定.
其中(2)和(3)本质相同,只是表达形式不同.解题时,灵活选用其中之一.
下雨天转动雨伞时飞出的水,以及在砂轮上打磨工件飞 出的火星,均沿着圆的切线的方向飞出. 1 当你在下雨天快速转动雨伞时水飞出的方向是什么方向?
2 砂轮打磨工件飞出火星的方向是什么方向?现在你知道:Class over
88!直线和圆相交d rd r 直线和圆相切直线和圆相离d r●O相交相切 相离┐dd┐d┐<=>知识回顾
同课章节目录
