1.3.1 函数的最大(小)值
文档属性
| 名称 | 1.3.1 函数的最大(小)值 |
|
|
| 格式 | rar | ||
| 文件大小 | 255.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-10 00:00:00 | ||
图片预览




文档简介
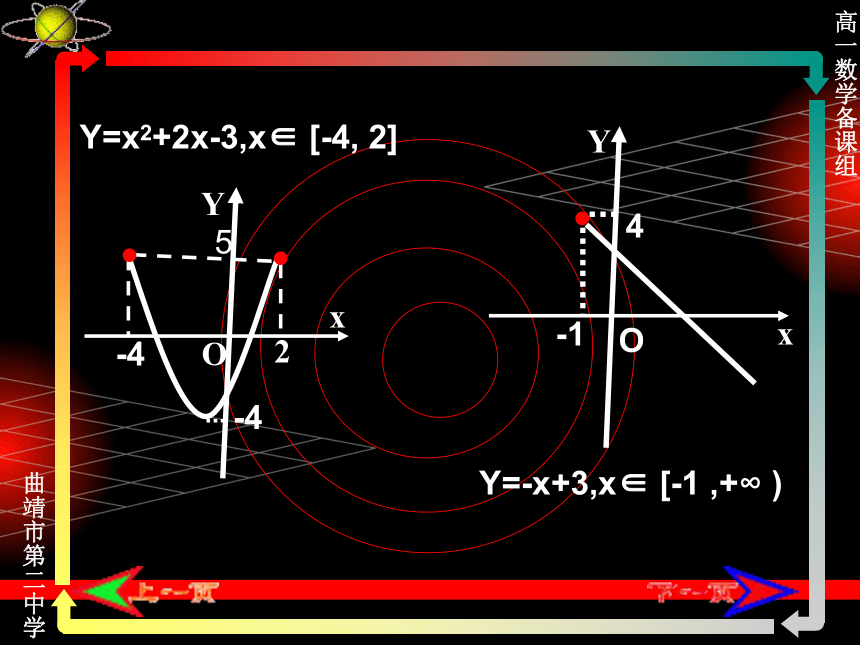
课件17张PPT。函数的最大(小)值高一数学备课组x函数f (x)=-x2 +3.
在(-∞, 0]上是增函数,
在[0, +∞)上是减函数.
当x≤0时,f (x) ≤ f (0),
x≥0时, f (x) ≤ f (0).
从而对任意x∈R,都有f (x) ≤ f (0).
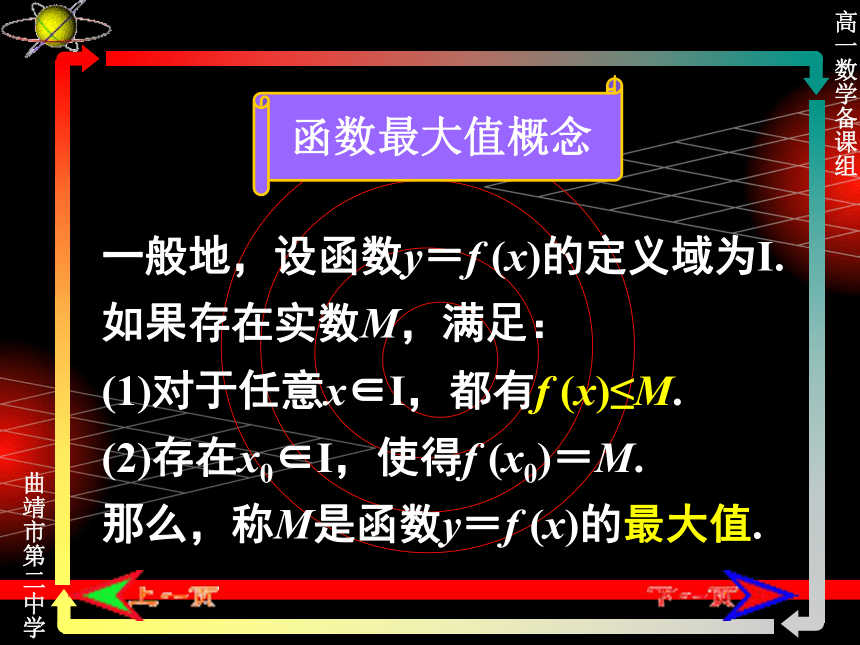
因此x=0时,f (0)是函数值中的最大值.YxY=-x2 +3O函数最大值概念一般地,设函数y=f (x)的定义域为I.
如果存在实数M,满足:
(1)对于任意x∈I,都有f (x)≤M.
(2)存在x0∈I,使得f (x0)=M.
那么,称M是函数y=f (x)的最大值.函数最小值概念一般地,设函数y=f (x)的定义域为I.
如果存在实数M,满足:
(1)对于任意x∈I,都有f (x) ≥M.
(2)存在x0∈I,使得f (x0)=M.
那么,称M是函数y=f (x)的最小值.例1 设f (x)是定义在区间[-6, 11]上的
函数. 如果f (x)在区间[-6, -2]上递减,在区间[-2, 11]上递增,画出f (x)的一
个大致的图象,从图象上可以发现f(-2)是函数f (x)的一个 .最小值f(11)是函数f (x)的最大值吗?问题一般化
设f (x)是定义在区间[a, b]上的函数. 如果f (x)在区间[a, c]上递减,在区间[c, b]上递增,那么f(c)是函数f (x)的一个最小值 .求函数的最大值和最小值.例2 已知函数y=(x∈[2,6]),有最值吗?如果有,试求出它. 函数y=(x∈[2,6]),你也能行问题一、是否每个函数都有最大值和最小值?举例说明。问题二、如果函数y=f(x)最大值是b,最小值是a,那么函数y=f(x)的值域是 [a,b]吗?问题与思考的最大值是 .1. 函数y=, x∈(-1,+∞)的值域是 ., x∈[2,4]2. 函数f(x)=我也能行[4[0,8] 是 .3.函数f(x)= 1的最小值4. 试猜想函数y= 的最值,并加于说明.小结(1)函数最大值或最小值就是函数图像上的最高点或最低点的纵坐标。 (2)利用函数的单调性求函数的最大值或最小值。谢谢指导!值域{5,10,15,20}
在(-∞, 0]上是增函数,
在[0, +∞)上是减函数.
当x≤0时,f (x) ≤ f (0),
x≥0时, f (x) ≤ f (0).
从而对任意x∈R,都有f (x) ≤ f (0).
因此x=0时,f (0)是函数值中的最大值.YxY=-x2 +3O函数最大值概念一般地,设函数y=f (x)的定义域为I.
如果存在实数M,满足:
(1)对于任意x∈I,都有f (x)≤M.
(2)存在x0∈I,使得f (x0)=M.
那么,称M是函数y=f (x)的最大值.函数最小值概念一般地,设函数y=f (x)的定义域为I.
如果存在实数M,满足:
(1)对于任意x∈I,都有f (x) ≥M.
(2)存在x0∈I,使得f (x0)=M.
那么,称M是函数y=f (x)的最小值.例1 设f (x)是定义在区间[-6, 11]上的
函数. 如果f (x)在区间[-6, -2]上递减,在区间[-2, 11]上递增,画出f (x)的一
个大致的图象,从图象上可以发现f(-2)是函数f (x)的一个 .最小值f(11)是函数f (x)的最大值吗?问题一般化
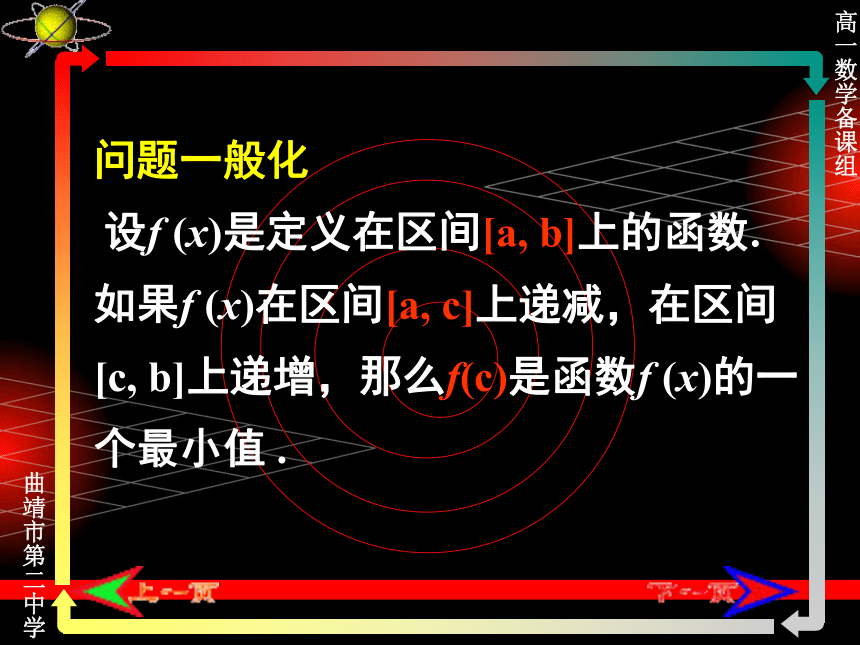
设f (x)是定义在区间[a, b]上的函数. 如果f (x)在区间[a, c]上递减,在区间[c, b]上递增,那么f(c)是函数f (x)的一个最小值 .求函数的最大值和最小值.例2 已知函数y=(x∈[2,6]),有最值吗?如果有,试求出它. 函数y=(x∈[2,6]),你也能行问题一、是否每个函数都有最大值和最小值?举例说明。问题二、如果函数y=f(x)最大值是b,最小值是a,那么函数y=f(x)的值域是 [a,b]吗?问题与思考的最大值是 .1. 函数y=, x∈(-1,+∞)的值域是 ., x∈[2,4]2. 函数f(x)=我也能行[4[0,8] 是 .3.函数f(x)= 1的最小值4. 试猜想函数y= 的最值,并加于说明.小结(1)函数最大值或最小值就是函数图像上的最高点或最低点的纵坐标。 (2)利用函数的单调性求函数的最大值或最小值。谢谢指导!值域{5,10,15,20}
