7.3.2多边形的内角和
文档属性
| 名称 | 7.3.2多边形的内角和 |

|
|
| 格式 | rar | ||
| 文件大小 | 609.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-10 00:00:00 | ||
图片预览


文档简介
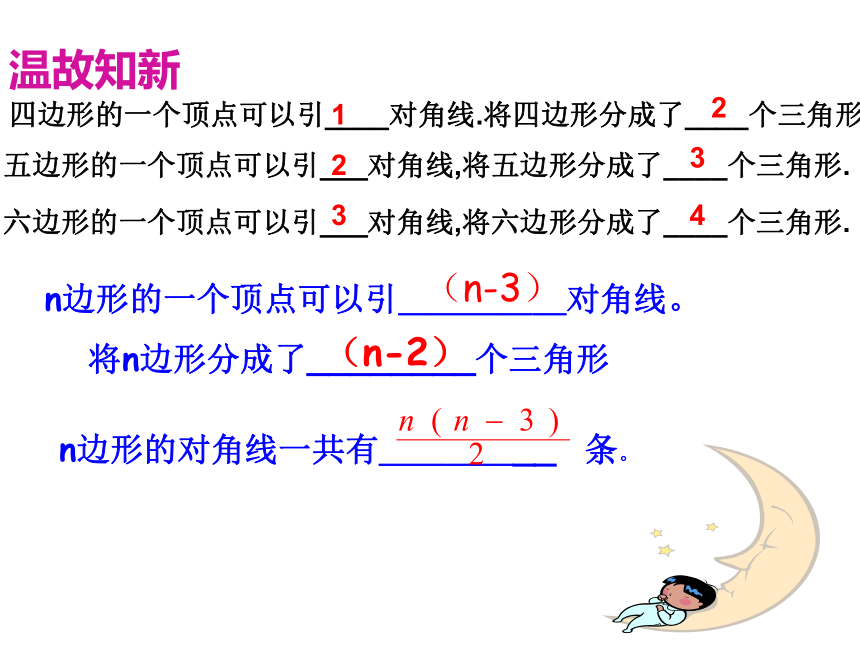
课件18张PPT。§7.3.2多边形的内角和五原六中 刘萍 n边形的一个顶点可以引_____对角线。
将n边形分成了________个三角形
n边形的对角线一共有______ 条。
(n-3)(n-2)温故知新四边形的一个顶点可以引____对角线.将四边形分成了____个三角形12五边形的一个顶点可以引___对角线,将五边形分成了____个三角形.23六边形的一个顶点可以引___对角线,将六边形分成了____个三角形.34问题2:你知道长方形和正方形的内角和是多少?
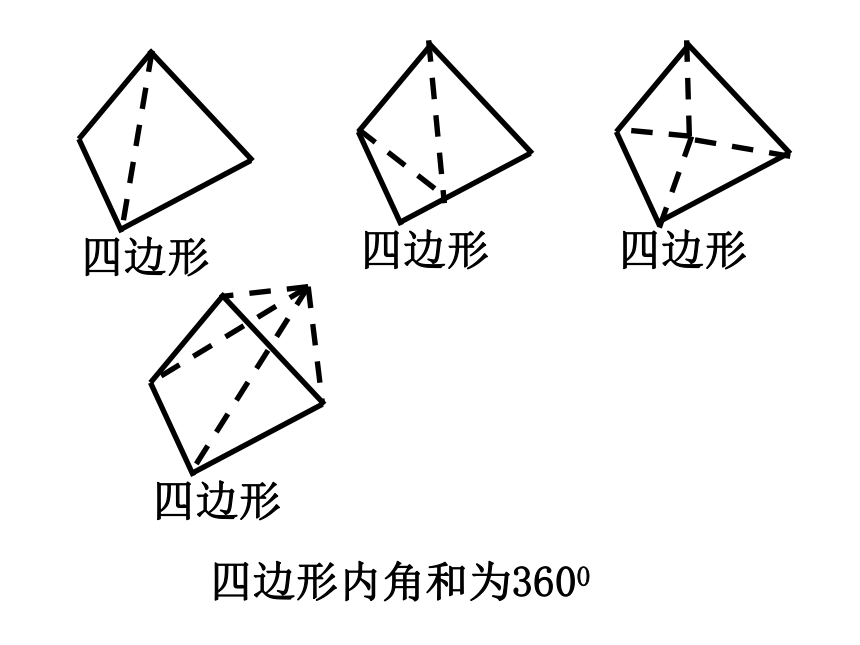
其它四边形的内角和是多少?
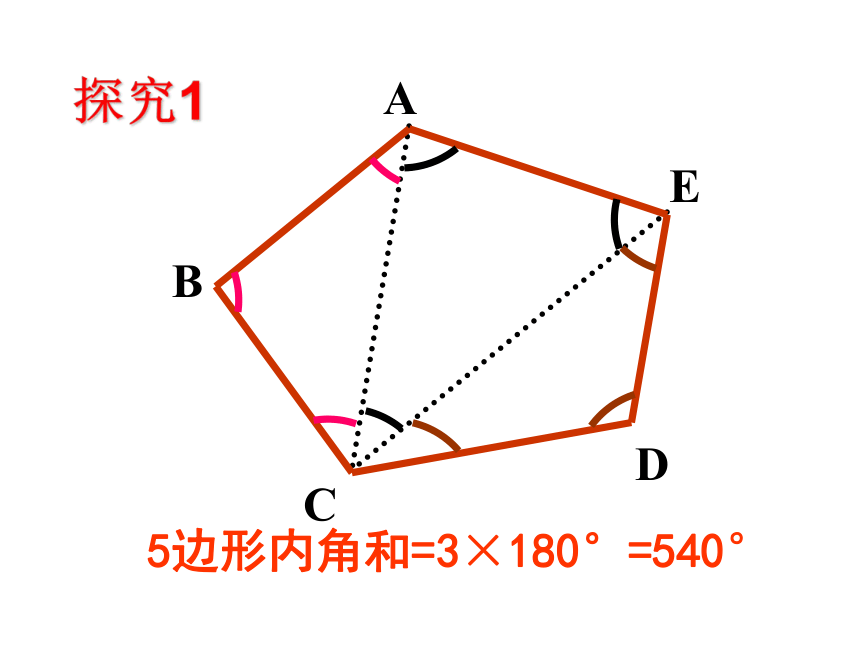
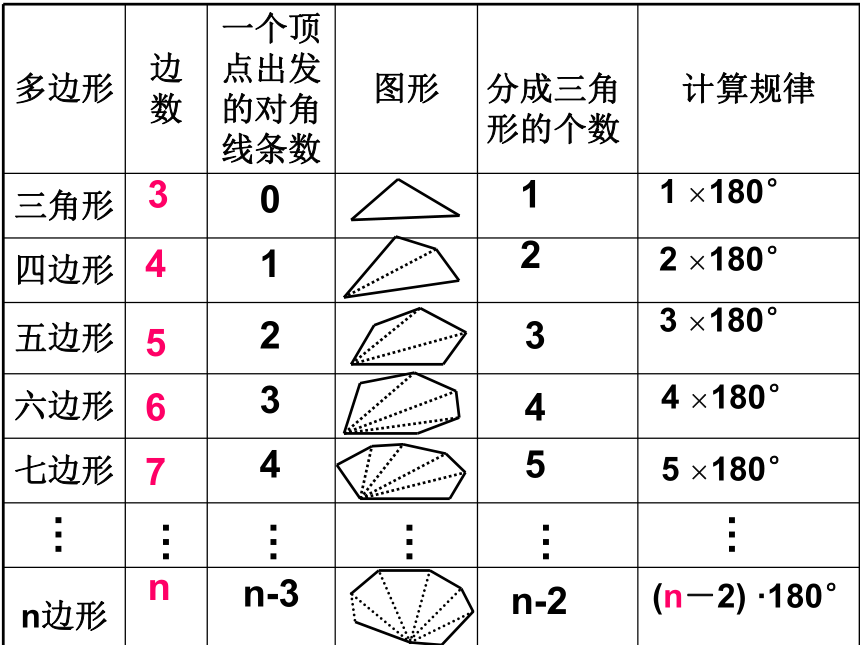
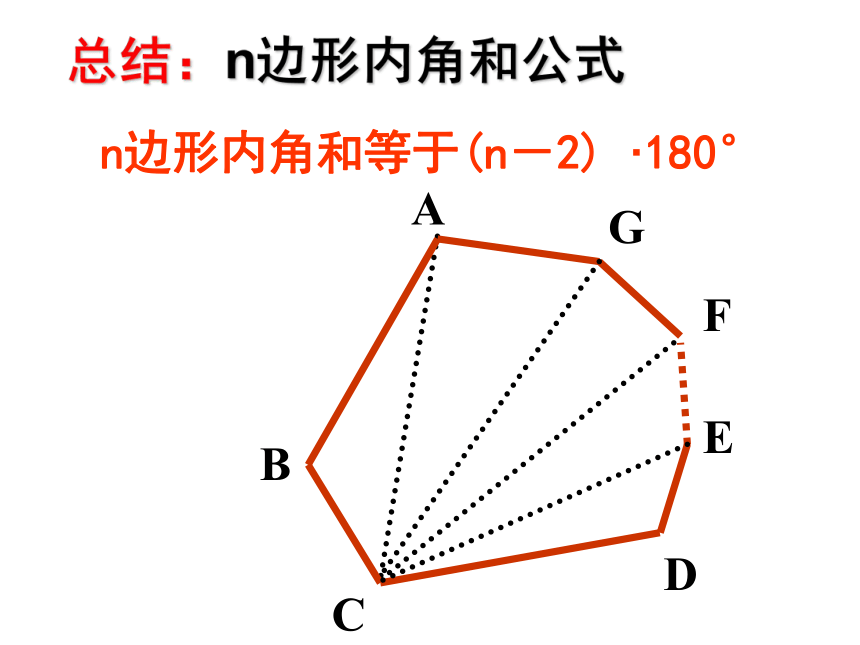
问题1:你还记得三角形内角和是多少度?(三角形内角和 180°)(都是360°)想一想四边形内角和为3600 B ACDE探究15边形内角和=3×180°=540°………………34567n0n-3123412345n-2(n-2) ·180°5 ×180°4 ×180°3 ×180°2 ×180°1 ×180°总结:n边形内角和公式n边形内角和等于(n-2) ·180°例1:已知四边形ABCD,∠A+∠C=180°,求∠B+∠D=?ABCD点评:四边形的一组对角互补,另一组对角也互补。解:四边形的内角和为:(4-2) ×180 =360 °∴ ∠B+∠D= 360 °- (A+∠C)=180° ∠A+∠C=180°十二边形的内角和是( )。
一个多边形当边数增加1时,它的内角和增加( )。
一个多边形的内角和是720o,则此多边形共有( )个内角。
如果一个多边形的内角和是1440度,那么这是( )边形。1800o180o六十 例1 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
1.任意一个外角和他相邻的内角有什么关系?
2.五个外角加上他们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系? 6 例1 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
5边形外角和 结论:五边形的外角和等于360°-(5-2) × 180°=360 ° 6=5个平角-5个内角和=5×180°探究在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.n边形外角和=结论:
n边形的外角和等于360°-(n-2) × 180°=360 °n个平角-n边形内角和=n×180 °从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。在行程中所转的各个角的和是多少?多边形的外角和回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?每个内角的度数是每个外角的度数是练一练练习1:正五边形的每一个外角等于____,每一个内角等于_____。5X=360°X=72°72°144°解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:所以每一个内角度数为108 °练习2: 已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。 解: 设多边形的边数为n
∵它的内角和等于 (n-2)?180°,
多边形外角和等于360o,
∴ (n-2)?180°=2× 360o。
解得: n=6
∴这个多边形的边数为6。
3.填空题
(1)一个多边形的内角和为4320°,则它的边数为______
(2)五边形的内角和为_____,它的对角线共有_____条
(3)一个多边形的每一个外角都等于30°,则这个多边形为____边形
(4)一个多边形的每一个内角都等于135°,则这个多边形为_____边形
(5)如果一个多边形的边数增加一条,那么这个多边形的内角和增加________,外角和增加_______.
拓展:
把一个四边形削去一个角,剩下一个几边形?它的内角和是多少?
将n边形分成了________个三角形
n边形的对角线一共有______ 条。
(n-3)(n-2)温故知新四边形的一个顶点可以引____对角线.将四边形分成了____个三角形12五边形的一个顶点可以引___对角线,将五边形分成了____个三角形.23六边形的一个顶点可以引___对角线,将六边形分成了____个三角形.34问题2:你知道长方形和正方形的内角和是多少?
其它四边形的内角和是多少?
问题1:你还记得三角形内角和是多少度?(三角形内角和 180°)(都是360°)想一想四边形内角和为3600 B ACDE探究15边形内角和=3×180°=540°………………34567n0n-3123412345n-2(n-2) ·180°5 ×180°4 ×180°3 ×180°2 ×180°1 ×180°总结:n边形内角和公式n边形内角和等于(n-2) ·180°例1:已知四边形ABCD,∠A+∠C=180°,求∠B+∠D=?ABCD点评:四边形的一组对角互补,另一组对角也互补。解:四边形的内角和为:(4-2) ×180 =360 °∴ ∠B+∠D= 360 °- (A+∠C)=180° ∠A+∠C=180°十二边形的内角和是( )。
一个多边形当边数增加1时,它的内角和增加( )。
一个多边形的内角和是720o,则此多边形共有( )个内角。
如果一个多边形的内角和是1440度,那么这是( )边形。1800o180o六十 例1 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
1.任意一个外角和他相邻的内角有什么关系?
2.五个外角加上他们分别相邻的五个内角和是多少?
3.这五个平角和与五边形的内角和、外角和有什么关系? 6 例1 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
5边形外角和 结论:五边形的外角和等于360°-(5-2) × 180°=360 ° 6=5个平角-5个内角和=5×180°探究在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.n边形外角和=结论:
n边形的外角和等于360°-(n-2) × 180°=360 °n个平角-n边形内角和=n×180 °从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。在行程中所转的各个角的和是多少?多边形的外角和回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?每个内角的度数是每个外角的度数是练一练练习1:正五边形的每一个外角等于____,每一个内角等于_____。5X=360°X=72°72°144°解:设正五边形的每一个外角度数为x,由
多边形的外角和等于360度可得:所以每一个内角度数为108 °练习2: 已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数。 解: 设多边形的边数为n
∵它的内角和等于 (n-2)?180°,
多边形外角和等于360o,
∴ (n-2)?180°=2× 360o。
解得: n=6
∴这个多边形的边数为6。
3.填空题
(1)一个多边形的内角和为4320°,则它的边数为______
(2)五边形的内角和为_____,它的对角线共有_____条
(3)一个多边形的每一个外角都等于30°,则这个多边形为____边形
(4)一个多边形的每一个内角都等于135°,则这个多边形为_____边形
(5)如果一个多边形的边数增加一条,那么这个多边形的内角和增加________,外角和增加_______.
拓展:
把一个四边形削去一个角,剩下一个几边形?它的内角和是多少?
