不等式的性质
图片预览




文档简介
课件21张PPT。相信自己加油!!!等式基本性质1:等式的两边都加上(或减去)同一个整式,等式仍旧成立等式基本性质2:
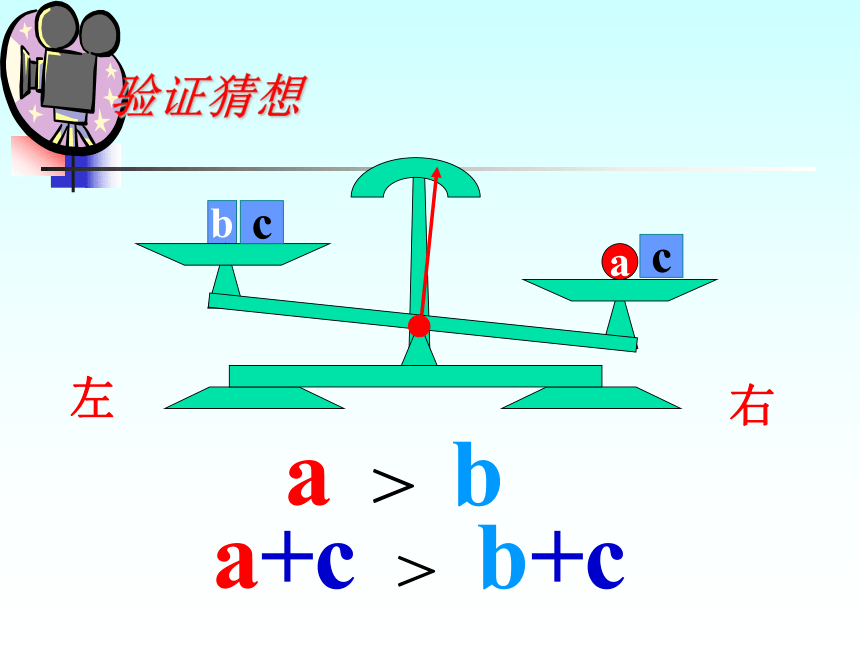
等式的两边都乘以(或除以)同一个不为0的数,等式仍旧成立温故知新不等式是否具有类似的性质呢? 不等式的基本性质五原六中 刘萍不等式是否具有类似的性质呢?由 3 <7想 3 +5 7+5想 3 -5 7-5你有什么发现?<<不等式的两边都加(或减)同一个数,
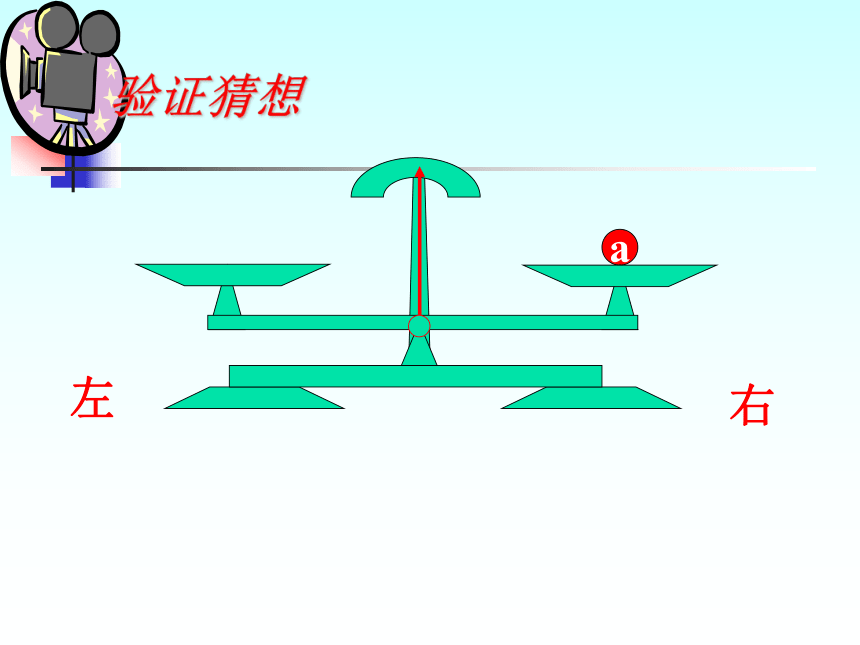
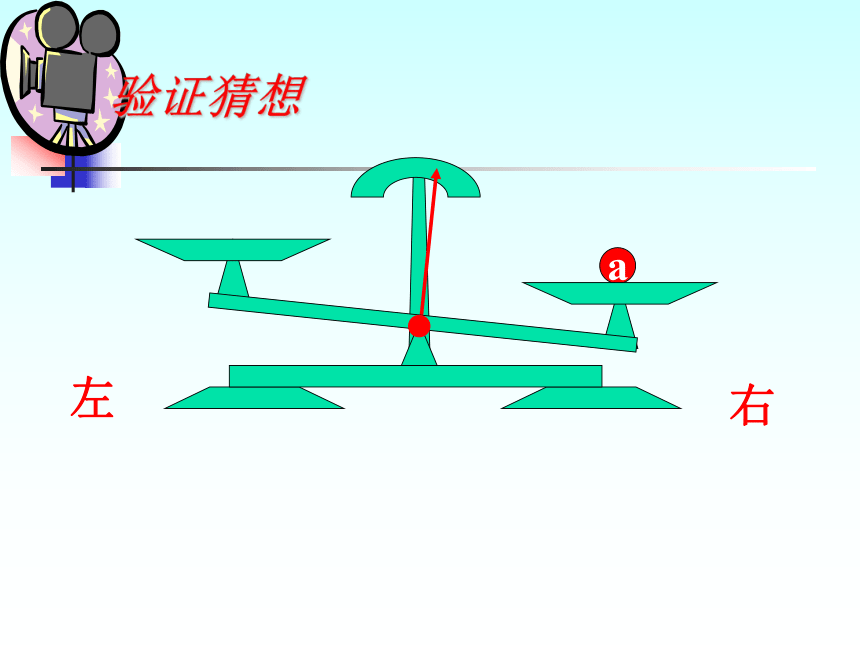
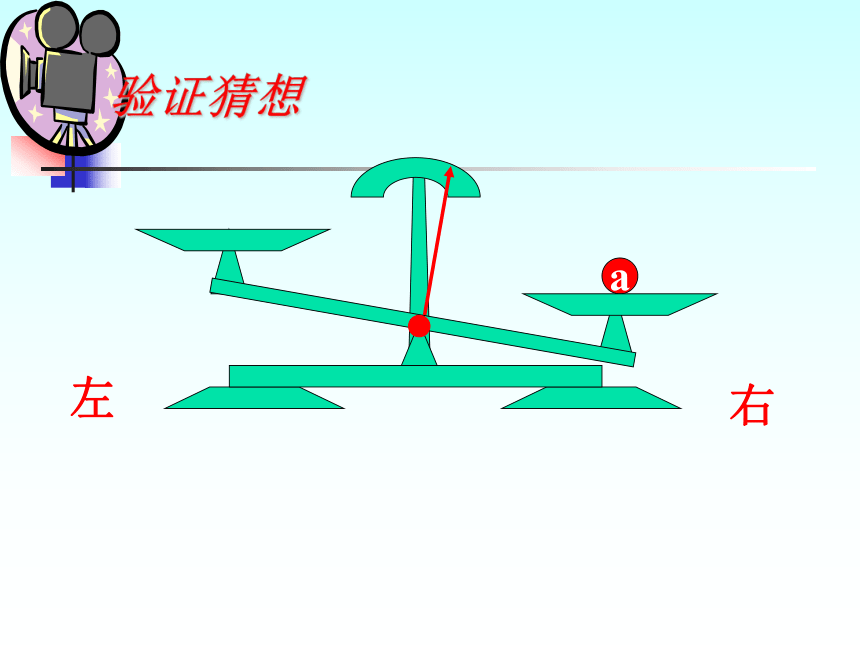
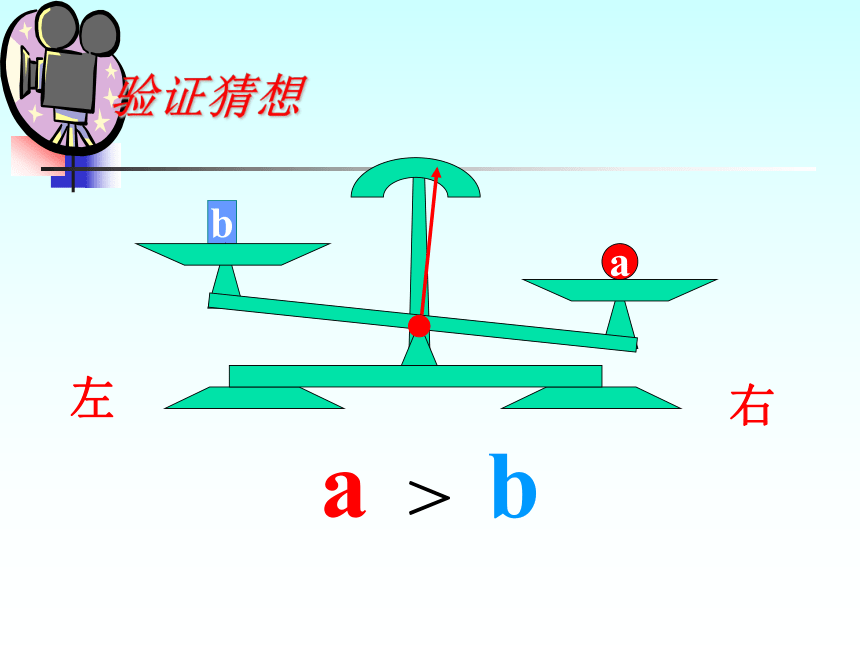
不等号的方向不变。a右左验证猜想a右左验证猜想a右左验证猜想ba右左a > b验证猜想ba右左cca+c > b+c验证猜想a > b 右左cc验证猜想a > b 右左a-c b-c>验证猜想a > b不等式两边加(或减)同一个数(或式子),
不等 号的方向不变。 如果a>b,那么a±c b±c
﹥规律探索不等式7>4-8<47×5 4×5-8÷2 4÷2不变不变两边都乘(或除以)
同一个数
不等式 不等式两边乘( 或除以)同一个正数,不等号的方向不变。>< 如果a<b,c>0那么ac bc,﹤﹤7>4-8÷(-2) 4÷(-2)7×(-5) 4×(-5)-8<4<>改变改变不等式性质2:不等式两边乘( 或除以)同一个负数,不等号的方向改变。不等式性质3:如果a<b,c<0那么ac bc,>>不等式性质1:
不等式两边加( 或减去 )同一个数(或式子),不等号的方向不变。
不等式性质2:
不等式两边乘( 或除以 )同一个正数,不等号的方向不变。
不等式性质3:
不等式两边乘( 或除以 )同一个负数,不等号的方向改变。
1、设a>b,用“<”或“>”填空:
(1)a-3 b-3 (2) (3) -4a -4b><>(4)2a-5____2b-5(5)-3a+1____-3b+1><
2.用“>”或“<”在横线上填空,并在题后
括号内填写理由.
∵a>b (2)∵ a>b
∴a-4 b-4( ) ∴ 4a 4b( )
(3)∵3m>5n (4)∵4x>5x
∴ -m ( ) ∴ x 0( )
(5)∵ < (6)∵a-1<8
∴ a 2b( ) ∴ a 9( ) >>><<<不等式基
本性质1不等式基
本性质3不等式基
本性质3不等式基
本性质1不等式基
本性质2不等式基
本性质1试试 练练 你能行!3.单项选择:
(1)由 x>y 得 ax>ay 的条件是( )
A.a>0 B.a<0 C.a≥0 D.a≤0
(2)由 x>y 得 ax≤ay 的条件是( )
A.a>0 B.a<0 C.a≥0 D.a≤0
(3)由 a>b 得 am2>bm2 的条件是( )
A.m>0 B.m<0 C.m≠0 D.m是任意有理数
(4)若 a>1,则下列各式中错误的是( )
A.4a>4 B.a+5>6 C. < D.a-1<0ADCD你太棒了!4.判断正误:
(1)∵a+8>4 (2)∵3>2
∴a>-4 ( ) ∴3a>2a( )
(3)∵-1>-2
∴a-1>a-2 ( ) √×√比一比,赛一赛把下列不等式化成x>a或x<a的形式
(1)x+2>3 (2)2x<-6
(3)3x<2x+1 (4)>1 锋 芒 初 试解:(1) x+2>3X+2-2 3 -2
得: X>1> 1、本节课我学到了什么知识, 都会了吗? 2、我还有哪些疑惑?回味无穷……
等式的两边都乘以(或除以)同一个不为0的数,等式仍旧成立温故知新不等式是否具有类似的性质呢? 不等式的基本性质五原六中 刘萍不等式是否具有类似的性质呢?由 3 <7想 3 +5 7+5想 3 -5 7-5你有什么发现?<<不等式的两边都加(或减)同一个数,
不等号的方向不变。a右左验证猜想a右左验证猜想a右左验证猜想ba右左a > b验证猜想ba右左cca+c > b+c验证猜想a > b 右左cc验证猜想a > b 右左a-c b-c>验证猜想a > b不等式两边加(或减)同一个数(或式子),
不等 号的方向不变。 如果a>b,那么a±c b±c
﹥规律探索不等式7>4-8<47×5 4×5-8÷2 4÷2不变不变两边都乘(或除以)
同一个数
不等式 不等式两边乘( 或除以)同一个正数,不等号的方向不变。>< 如果a<b,c>0那么ac bc,﹤﹤7>4-8÷(-2) 4÷(-2)7×(-5) 4×(-5)-8<4<>改变改变不等式性质2:不等式两边乘( 或除以)同一个负数,不等号的方向改变。不等式性质3:如果a<b,c<0那么ac bc,>>不等式性质1:
不等式两边加( 或减去 )同一个数(或式子),不等号的方向不变。
不等式性质2:
不等式两边乘( 或除以 )同一个正数,不等号的方向不变。
不等式性质3:
不等式两边乘( 或除以 )同一个负数,不等号的方向改变。
1、设a>b,用“<”或“>”填空:
(1)a-3 b-3 (2) (3) -4a -4b><>(4)2a-5____2b-5(5)-3a+1____-3b+1><
2.用“>”或“<”在横线上填空,并在题后
括号内填写理由.
∵a>b (2)∵ a>b
∴a-4 b-4( ) ∴ 4a 4b( )
(3)∵3m>5n (4)∵4x>5x
∴ -m ( ) ∴ x 0( )
(5)∵ < (6)∵a-1<8
∴ a 2b( ) ∴ a 9( ) >>><<<不等式基
本性质1不等式基
本性质3不等式基
本性质3不等式基
本性质1不等式基
本性质2不等式基
本性质1试试 练练 你能行!3.单项选择:
(1)由 x>y 得 ax>ay 的条件是( )
A.a>0 B.a<0 C.a≥0 D.a≤0
(2)由 x>y 得 ax≤ay 的条件是( )
A.a>0 B.a<0 C.a≥0 D.a≤0
(3)由 a>b 得 am2>bm2 的条件是( )
A.m>0 B.m<0 C.m≠0 D.m是任意有理数
(4)若 a>1,则下列各式中错误的是( )
A.4a>4 B.a+5>6 C. < D.a-1<0ADCD你太棒了!4.判断正误:
(1)∵a+8>4 (2)∵3>2
∴a>-4 ( ) ∴3a>2a( )
(3)∵-1>-2
∴a-1>a-2 ( ) √×√比一比,赛一赛把下列不等式化成x>a或x<a的形式
(1)x+2>3 (2)2x<-6
(3)3x<2x+1 (4)>1 锋 芒 初 试解:(1) x+2>3X+2-2 3 -2
得: X>1> 1、本节课我学到了什么知识, 都会了吗? 2、我还有哪些疑惑?回味无穷……
