圆的对称性--垂径定理推论

垂径定理推论
学习目的：掌握垂径定理的两个推论
学习过程：
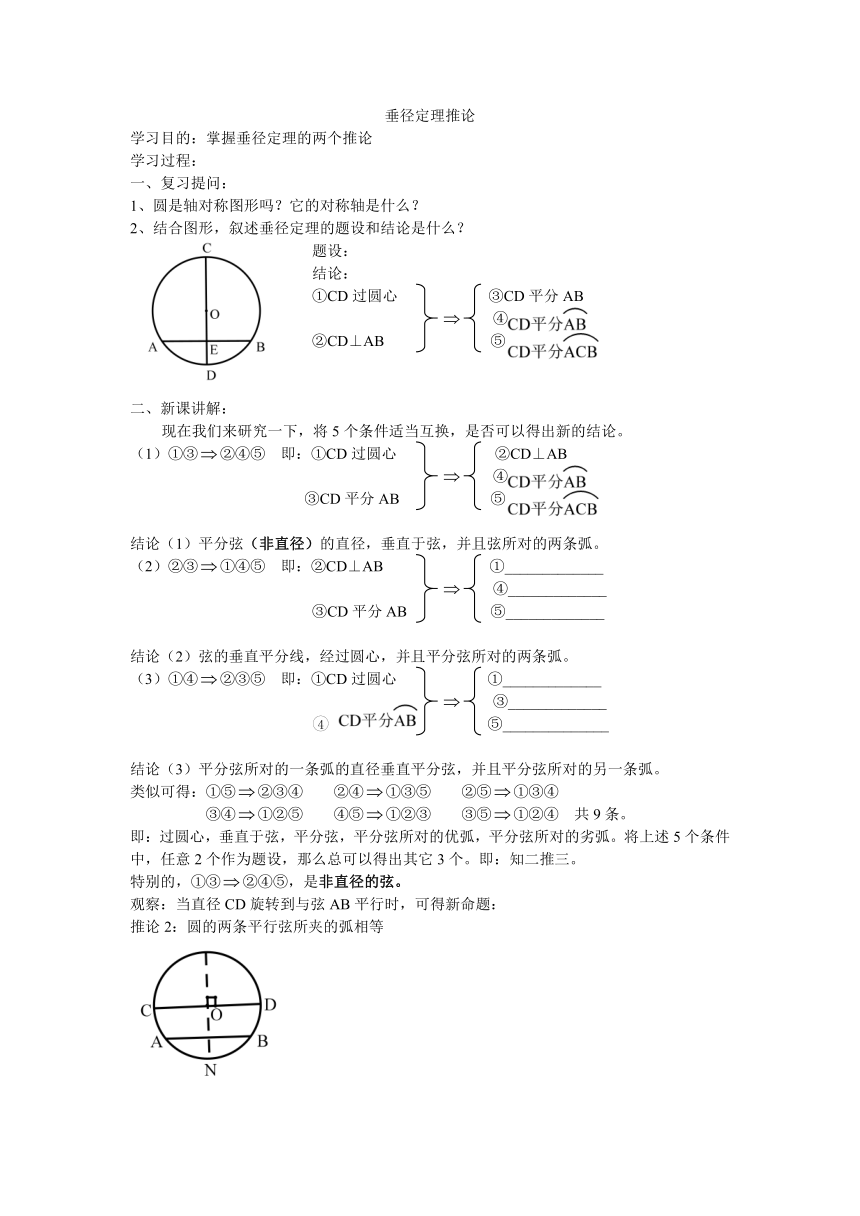
一、复习提问：
1、圆是轴对称图形吗？它的对称轴是什么？
2、结合图形，叙述垂径定理的题设和结论是什么？
题设：
结论：
①CD过圆心 ③CD平分AB
　　 　　④
　　　　　　　　　　　　②CD⊥AB　　　　　　　⑤
二、新课讲解：
现在我们来研究一下，将5个条件适当互换，是否可以得出新的结论。
（1）①③②④⑤ 即：①CD过圆心 ②CD⊥AB
④
③CD平分AB　　　　　　⑤
结论（1）平分弦（非直径）的直径，垂直于弦，并且弦所对的两条弧。
（2）②③①④⑤ 即：②CD⊥AB ①_____________
　 ④_____________
③CD平分AB　　　　　 ⑤_____________
结论（2）弦的垂直平分线，经过圆心，并且平分弦所对的两条弧。
（3）①④②③⑤ 即：①CD过圆心 ①_____________
　　③_____________
4 ⑤______________
结论（3）平分弦所对的一条弧的直径垂直平分弦，并且平分弦所对的另一条弧。
类似可得：①⑤②③④　　②④①③⑤　　②⑤①③④　　
　　　　　③④①②⑤　　④⑤①②③　　③⑤①②④ 共9条。
即：过圆心，垂直于弦，平分弦，平分弦所对的优弧，平分弦所对的劣弧。将上述5个条件中，任意2个作为题设，那么总可以得出其它3个。即：知二推三。
特别的，①③②④⑤，是非直径的弦。
观察：当直径CD旋转到与弦AB平行时，可得新命题：
推论2：圆的两条平行弦所夹的弧相等
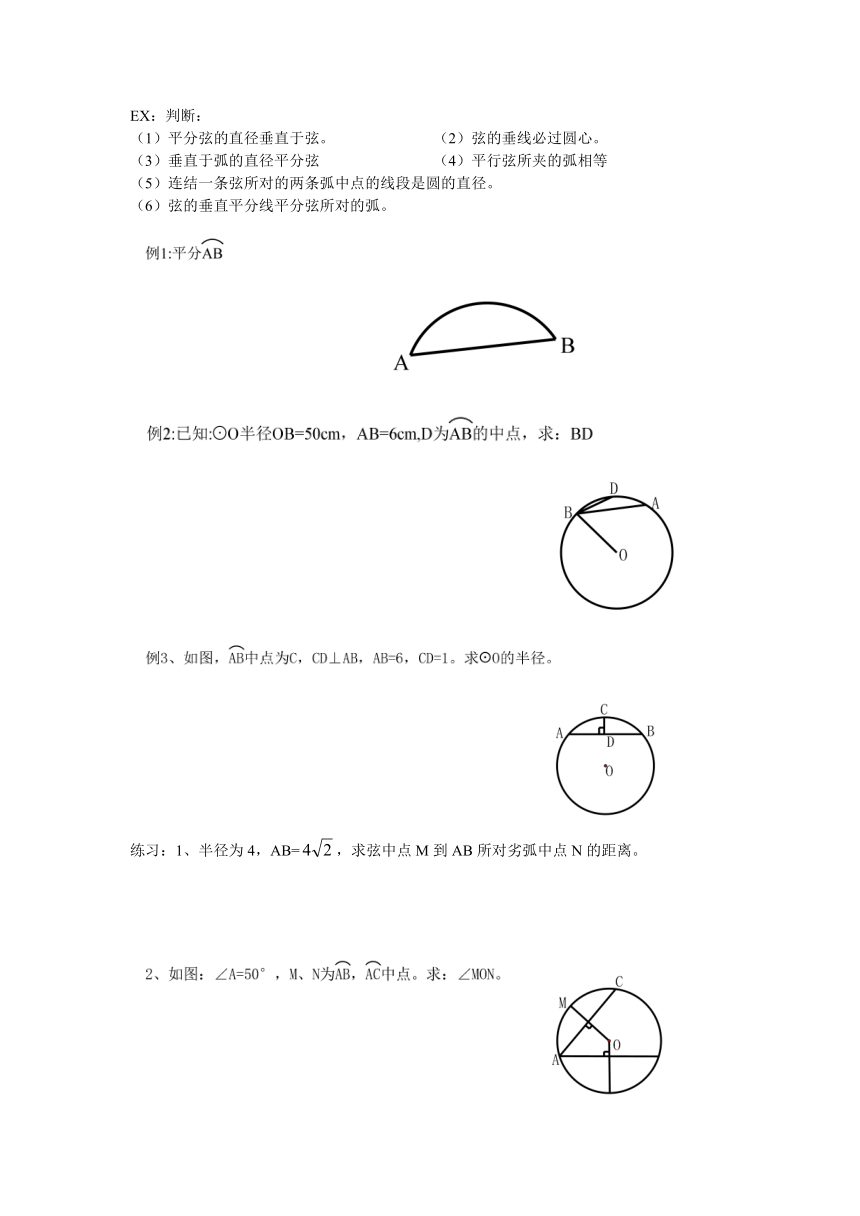
EX：判断：
（1）平分弦的直径垂直于弦。 （2）弦的垂线必过圆心。
（3）垂直于弧的直径平分弦 （4）平行弦所夹的弧相等
（5）连结一条弦所对的两条弧中点的线段是圆的直径。
（6）弦的垂直平分线平分弦所对的弧。
练习：1、半径为4，AB=，求弦中点M到AB所对劣弧中点N的距离。
3、OA=10，C为AB中点，OC∶AC=3∶4。求：AB。
4、M、N为AB、CD中点，∠AMN=∠CNM。求证：AB=CD。
5、OA=OB。求证：AC=BD
作业：
2、⊙O半径为10，AB⊥CD，AE=4，BE=8。求：CD。
3、如图：AB∥CD，相距22，AB=40，CD=48。求：⊙O的半径。
4、M、N为AB、CD中点，∠AMN=∠CNM。求证：OM=ON。
5、如图：直径AB=4，∠A=30°。求AC。
6、如图：OM=4，ON=3。求：AB、CD、r。