轴对称图形复习教案

第一章复习 第 4 页
第一课时
考点1：轴对称及轴对称图形的意义
一、知识点：
1．轴对称： 2．轴对称图形： 3．轴对称的性质：
4．简单的轴对称图形：
线段：有两条对称轴：线段所在直线和线段中垂线． 角：有一条对称轴：该角的平分线所在的直线．
等腰(非等边）三角形：有一条对称轴，底边中垂线． 等边三角形：有三条对称轴：每条边的中垂线．
等腰梯形：过两底中点的直线 正n边形有n条对称轴
圆有无数条对称轴。
二、基本图形：
1．已知：点A、B分别在直线l的同侧，在直线l上找一点P，使PA+PB最短。
变形1：正方形ABCD中，点E是AB边上的一点，在对角线AC上找一点P，使PA+PB最短。
变形2：已知点A（1，6）、点B（6，4），在x轴和y轴上各找一点C、D，使四边形ACDB的周长最短。
三、经典考题剖析：
1．（2006无锡市3分）在下面四个图案中，如果不考虑图中的文字和字母，那么不是轴对称图形的是（　　）
4．（2006鸡西市3分）在下列四个图案中，既是轴对称图形，又是中心对称图形的是( )
6．（2006梅州市3分）小明在镜中看到身后墙上的时钟，实际时间最接近8时的是下图中的（　　）
11．(2006十堰市3分)如图，在平面直角坐标系中，请按下列要求分别作出变换后的图形（图中每个小正方形的边长为个单位）：
（1）向右平移个单位；（2）关于轴对称；（3）绕点顺时针方向旋转．
考点2：折叠问题
一、考点讲解：
常见的折叠问题有两种类型：一种是将一个图形沿着某一条直线折叠到另一个位置，这时候，这条直线两旁的图形全等；另一种是将一个图形沿着某一条直线折叠，使两个点重合，此时，这折痕所在的直线是这两点连线的垂直平分线。
二、基本图形：
1．将矩形ABCD沿着对角线AC对折，则三角形AFC是 三角形。
变形：若矩形ABCD中，AB=6，AD=3，求三角形AFC的面积。
2．将矩形ABCD沿着EF对折，使点B与点D重合，若AB=8，AD=10，求折痕EF的长。
三、典型例题剖析：
2．（2006内江市3分）如图（1）将矩形纸片ABCD沿AE折叠，使点B落在直角梯形AECD的中位线FG上，若AB=，则AE的长为( )
A. B. 3 C. 2 D.
6．（2006汉川市3分）将正方形纸片两次对折，并剪出一个菱形小洞后铺平，得到的图形是
7．（2006郴州市10分）如图7，矩形纸片的边长分别为．将纸片任意翻折（如图8），折痕为．（在上），使顶点落在四边形内一点，的延长线交直线于，再将纸片的另一部分翻折，使落在直线上一点，且所在直线与所在直线重合（如图9）折痕为．
（1）猜想两折痕之间的位置关系，并加以证明．
（2）若的角度在每次翻折的过程中保持不变，则每次翻折后，两折痕间的距离有何变化？请说明理由．
（3）若的角度在每次翻折的过程中都为（如图10），每次翻折后，非重叠部分的四边形，及四边形的周长与有何关系，为什么？
第二课时
考点3：线段的垂直平分和角的平分线
一、知识点：
1． 线段垂直分线：
（1）定义：（2）线段垂直平分线上的点；到线段两端距离相等的点
２．角的平分线：
（1）角平分线上的点；到角两边距离相等的点。
二、基本图形：
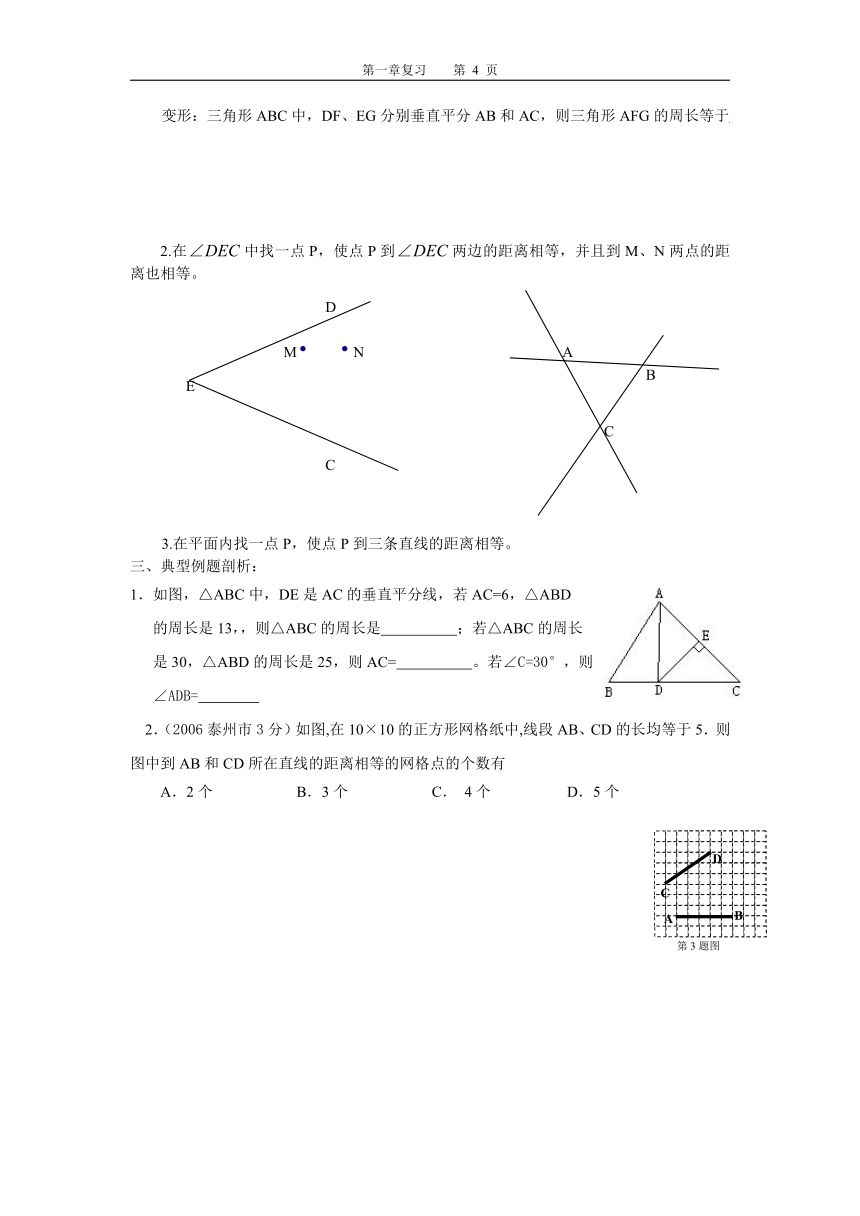
1.三角形ABC中，DE垂直平分AC，则三角形BCD的周长等于
变形：三角形ABC中，DF、EG分别垂直平分AB和AC，则三角形AFG的周长等于
2.在中找一点P，使点P到两边的距离相等，并且到M、N两点的距离也相等。
3.在平面内找一点P，使点P到三条直线的距离相等。
三、典型例题剖析：
1．如图，△ABC中，DE是AC的垂直平分线，若AC=6，△ABD
的周长是13，，则△ABC的周长是 ；若△ABC的周长
是30，△ABD的周长是25，则AC= 。若∠C=30°，则
∠ADB=
2．（2006泰州市3分）如图,在10×10的正方形网格纸中,线段AB、CD的长均等于5．则图中到AB和CD所在直线的距离相等的网格点的个数有
A．2个 B．3个 C． 4个 D．5个
第三课时
考点4：等腰三角形
一、知识点：
1．等腰三角形：（1）定义：（2）性质：（3）判定：
2．等边三角形：（1）定义：（2）性质：（3）判定：
3．直角三角形：（1）定义：。（2）性质：（3）判定：
二、基本图形：
1．等腰三角形一腰上的高与底边的夹角与顶角的关系。
变形：等腰三角形一腰上的高与另一腰的夹角与顶角的关系。
2．在三角形ABC中，AB=AC，点P是BC边上的任意一点，PM⊥AB,PN⊥AC,垂足分别为M、N，BD是AC边上的高，则PM+PN= 。
变形1：矩形ABCD中，PM⊥BD，PN⊥AC，若AB=3，BC=4，则PM+PN=
变形2：正方形ABCD中，AB=2，BC=BE，PM⊥BD，PN⊥BC，则PM+PN=
3．△ABC中，BD平分∠ABC，DE∥BC，则△BDE是 三角形。
变形1：BD、CD分别平分∠ABC和∠ACB，MN∥BC，则BM+CN=
变形2：BD、CD分别平分∠ABC和∠ACB的外角，MN∥BC，则BM-CN=
变形3：BD、CD分别平分∠ABC的外角和∠ACB的外角，MN∥BC，则BM+CN=
三、典型例题剖析
1：若等腰三角形一个角为72°，则顶角为 。
若等腰三角形的一个角是另一个角的2倍少10°，则顶角为 。
若等腰三角形的两条边长分别是3、6，则周长是 。
3．（2006扬州市10分）如图, △ABC中, D、E分别是AC、AB上的点, BD与CE交于点O. 给出下列三个条件：
①∠EBO＝∠DCO；②∠BEO＝∠CDO；③BE＝CD.
⑴ 上述三个条件中, 哪两个条件可判定△ABC是等腰三角形(用序号写出所有情形)；
⑵ 选择第⑴小题中的一种情形, 证明△ABC是等腰三角形.
4．（2006常德市8分）如图7，是等边三角形内的一点，连结，以为边作，且，连结．
（1）观察并猜想与之间的大小关系，并证明你的结论．（4分）
（2）若，连结，试判断的形状，并说明理由．（4分）
7．(2006日照8分）
如图，已知，等腰Rt△OAB中，∠AOB=90o，等腰Rt△EOF中，∠EOF=90o，连结AE、BF．
求证：（1）AE=BF；
（2）AE⊥BF．
第四课时
考点5：等腰梯形
一、考点讲解：
1．梯形：
（1）定义：（2）分类：
2．等腰梯形：（1）定义：（2）性质：（3）判定：
二、基本图形：
1．等腰梯形中，∠B=，则BC=AD+AB
2．等腰梯形中，若AB=AD=CD，则BD平分∠ABC
三、典型例题剖析：
1．（2006新疆维吾尔自治区3分）如图，等腰梯形下底与上底的差恰好等于腰长，．则等于（　　）
Ａ． Ｂ． Ｃ． Ｄ．
2．（2006徐州市2分）如图2，用四个全等的等腰梯形拼成四边形ABCD，则∠A＝
3．（2006深圳市７分）如图7，在梯形ABCD中，AD∥BC, HYPERLINK "http://" EMBED Equation.3 ，
．（1）（３分）求证：
（2）（４分）若，求梯形ABCD的面积．
4．（2006钦州市8分）已知：如图，在等腰梯形中，中，点分别在上，且．求证：．
5．（2006贵州黔南10分）如图，梯形中，，，为梯形外一点，分别交线段于点，且．
（1）写出图中三对你认为全等的三角形（不再添加辅助线）
（2）选择你在（1）中写出全等三角形中任意一对进行证明．
16．（2006常州市7分）已知：如图，△ABC和△ECD都是等腰直角三角形，，D为AB边上一点，
求证：（1）△ACE≌△BCD；（2）
思考题
21．（2006连云港市12分）操作与探究：
（1）图①是一块直角三角形纸片。将该三角形纸片按如图方法折叠，是点A与点C重合，DE为折痕。试证明△CBE等腰三角形；
（2）再将图①中的△CBE沿对称轴EF折叠(如图②)。通过折叠，原三角形恰好折成两个重合的矩形，其中一个是内接矩形，另一个是拼合(指无缝无重叠)所成的矩形，我们称这样的两个矩形为“组合矩形”。你能将图③中的△ABC折叠成一个组合矩形吗？如果能折成，请在图③中画出折痕；
（3）请你在图④的方格纸中画出一个斜三角形，同时满足下列条件：①折成的组合矩形为正方形；②顶点都在格点(各小正方形的顶点)上；
（4）有一些特殊的四边形，如菱形，通过折叠也能折成组合矩形(其中的内接矩形的四个顶点分别在原四边形的四条边上)。请你进一步探究，一个非特殊的四边形(指除平行四边形、梯形外的四边形)满足何条件是，一定能折成组合矩形？
22．如图，在等腰梯形中，，，，．等腰直角三角形的斜边，点与点重合，和在一条直线上，设等腰梯形不动，等腰直角三角形沿所在直线以的速度向右移动，直到点与点重合为止．
（1）等腰直角三角形在整个移动过程中与等腰梯形重叠部分的形状由 形变化为 形；
（2）设当等腰直角三角形移动时，等腰直角三角形与等腰梯形重叠部分的面积为，求与之间的函数关系式；
（3）当时，求等腰直角三角形与等腰梯形重叠部分的面积．
A
B
C
D
P
A
B
l
A
B
A．
B．
C．
D．
（第11题图）
B
A
C
D
E
F
A
B
C
D
E
F
B`
B′
F
E
G
D
C
B
A
P
C
Q
D
M
A
D
C
B
A
B
M
D
Q
C
P
Ａ
B
N
M
D
Q
C
P
Ａ
B
N
A
D
C
B
a
b
图7
图8
图9
图10
A
C
E
B
D
A
B
C
D
E
F
G
E
D
C
M
N
A
B
C
A
D
C
B
第3题图
A
M
N
B
C
D
A
M
N
B
C
D
P
P
M
N
P
A
B
C
D
E
图7
Q
C
P
A
B
第7题
图2
A
D
B
C
图7
A
B
F
C
D
E
(第28题图)
A
A
A
B
C
B
B
D
C
E
E
D
C
F
图①
图②
图③
图④
A
（N）
M
P
D
C
B
A
N
M
P
D
C
B