等边三角形
图片预览



文档简介
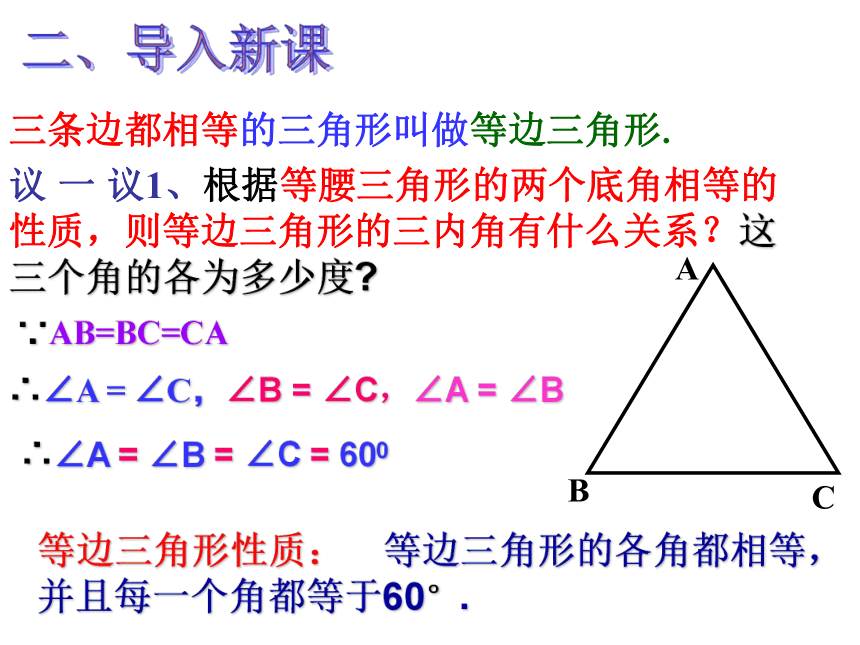
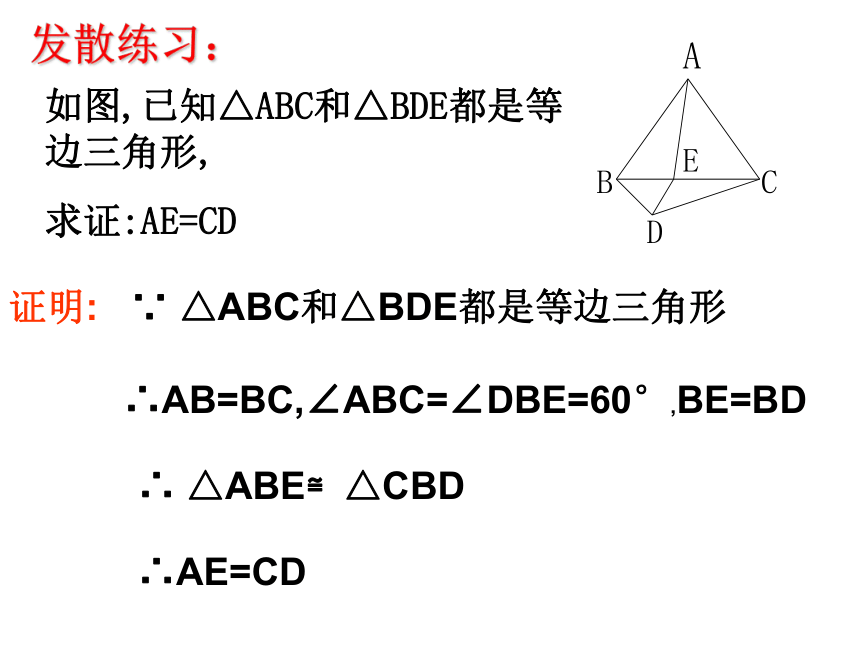
课件15张PPT。等边三角形的性质和判定1、等腰三角形的性质定理是什么?性质1:等腰三角形的两个底角相等。(等边对等角)性质2: 等腰三角形的顶角的平分线,底边上的中线,底边上的高互相重合。2、等腰三角形的判定定理:如果一个三角形中有两个角相等,那么这两个角所对的边也相等.(简称为:等角对等边 )一、温故知新 三条边都相等的三角形叫做等边三角形. 议 一 议1、根据等腰三角形的两个底角相等的性质,则等边三角形的三内角有什么关系?这三个角的各为多少度?ACB∵AB=BC=CA∴∠A = ∠C,∠B = ∠C,∠A = ∠B∴∠A = ∠B = ∠C = 600等边三角形性质: 等边三角形的各角都相等,并且每一个角都等于60°.二、导入新课如图,已知△ABC和△BDE都是等边三角形,
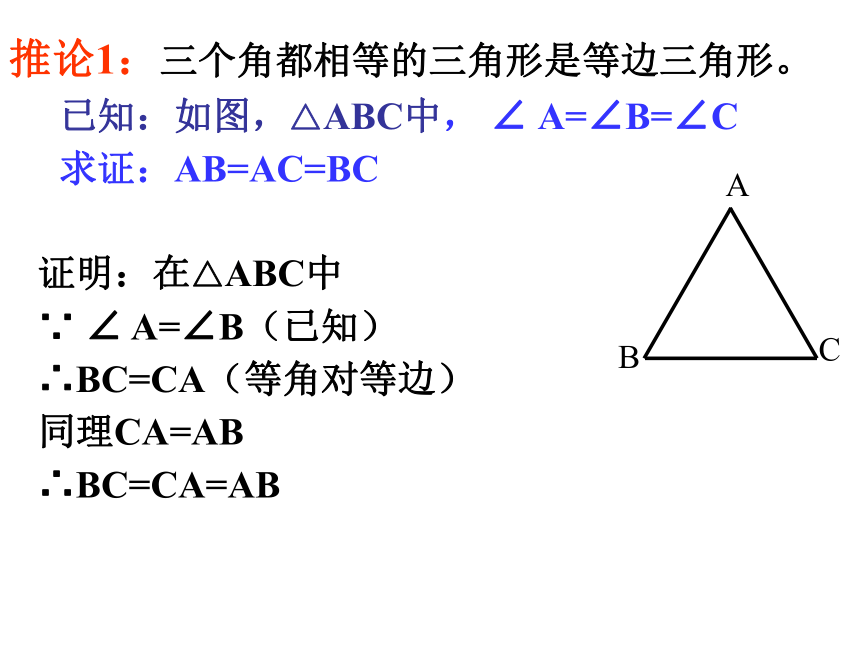
求证:AE=CD证明:∵ △ABC和△BDE都是等边三角形∴AB=BC,∠ABC=∠DBE=60°,BE=BD∴ △ABE≌△CBD∴AE=CD发散练习:推论1:三个角都相等的三角形是等边三角形。已知:如图,△ABC中, ∠ A=∠B=∠C
求证:AB=AC=BCABC证明:在△ABC中
∵ ∠ A=∠B(已知)
∴BC=CA(等角对等边)
同理CA=AB
∴BC=CA=AB
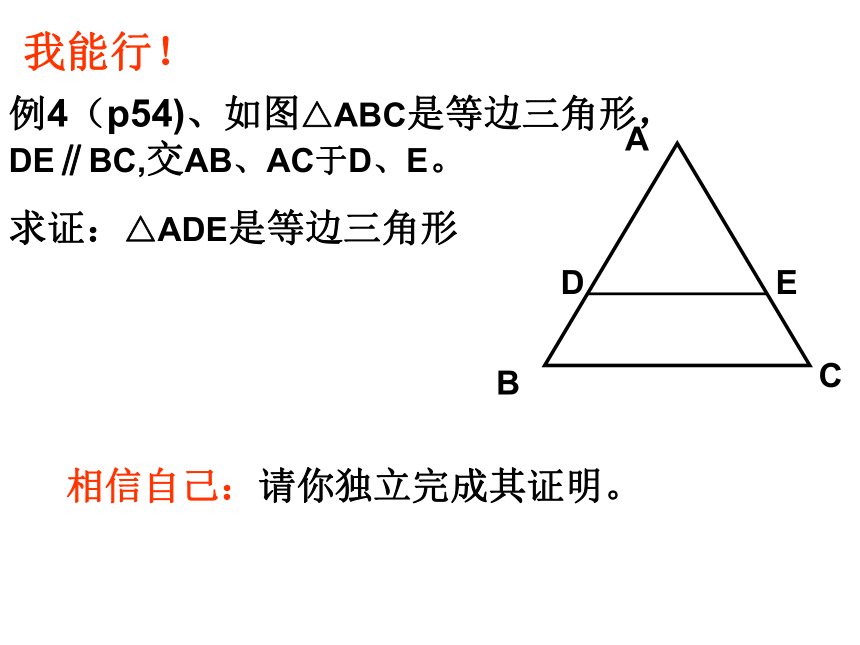
例4(p54)、如图△ABC是等边三角形,DE∥BC,交AB、AC于D、E。
求证:△ADE是等边三角形相信自己:请你独立完成其证明。我能行! 议 一 议2、你认为一个等腰三角形满足什么条件时便成为等边三角形?请把你的结论与同伴交流。猜想:有一个角等于60°的等腰三角形是等边三角形吗?你能证明你的结论吗?把你的证明思路与同伴进行交流。第一种情况:当顶角是600时第二种情况:当底角是60°时已知: ⊿ABC中,AB=AC, ∠ A=600。
求证:AB=AC=BCABC证明: ⊿ABC中
∵AB=AC,
∴ ∠B=∠C (等边对等角)
∵ ∠ A=600
∴ ∠B=∠C = 600
∴AB=AC=BC第一种情况:当顶角是600时温馨提示:第二种情况,当底角是60°时,请大家课后独立完成。推论⒉ 有一个角是60°的等腰三角形是等边三角形.如图,将两个含有30°角的三角形放在一起,你能借助这个图形,找到Rt△ABC与斜边AB之间的数量关系吗?
证明 ∵△ABC与△ADC关于AC轴对称∴AB=AD且AC⊥BD又∵∠BAD=2X30°=60°∴△ABD是等边三角形又∵AB=AD,AC⊥BD∴BC=1/2AB=1/2AD定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
三、操作思考,探索新知例5(p55) 下图是屋架设计图的一部分,点D是斜AB的中点,立柱BC、 DE垂直于横梁AC,
AB=7.4m,∠A=30°立柱BC 、 DE要多长?AB解:∵DE⊥AC, BC⊥AC, ∠A=30°得 BC=1/2AB, DE=1/2AD∴BC=1/2 ×7.4=3.7m又 AD=1/2 AB=3.7m ∴DE=1/2 AD=1/2 ×3.7=1.85m答:立柱BC的长是3.7m,DE的长是1.85m.四、范例点击 补例:等腰三角形的底角为15°,腰长为2a,求腰上的高。 已知:如图,在△ABC中,AB=AC=2a, ∠B=15 °, CD是腰AB上的高. 求CD的长。解:∵AB=AC∴∠B=∠ACB=15°∴∠DAC=30°∵CD⊥BD∴CD=1/2AC=a1、在△ABC中,AB=AC,∠C=30°,DA⊥BA于A,
BC=15,求AD的长 解:∵AB=AC∴∠B=∠C=30°∵DA⊥BA∴AD=1/2BD , ∠ADB=60°∵ ∠ADB=60° ∠C=30°∴∠DAC= ∠C=30°∴AD=DC=1/2BD∵BC=15∴AD=DC=5五、延伸拓展2、已知:如图,在等腰△ABC中,AB=AC ∠BAC=120° D为BC中点,DE⊥AB于E.证明:
∵AB=AC, ∠BAC=120°
∴∠B =30° ∵ AB=AC, D为BC中点, ∴AD⊥BC(三线合一)∵DE⊥AB∴AD=1/2AB ,∠BAD=60°等边三角形性质: 等边三角形的各角都相等,并且每一个角都等于60°.推论1:三个角都相等的三角形是等边三角形。推论⒉ 有一个角是60°的等腰三角形是等边三角形.定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.六、知识小结作业:p58 11
p58 13谢谢大家
求证:AE=CD证明:∵ △ABC和△BDE都是等边三角形∴AB=BC,∠ABC=∠DBE=60°,BE=BD∴ △ABE≌△CBD∴AE=CD发散练习:推论1:三个角都相等的三角形是等边三角形。已知:如图,△ABC中, ∠ A=∠B=∠C
求证:AB=AC=BCABC证明:在△ABC中
∵ ∠ A=∠B(已知)
∴BC=CA(等角对等边)
同理CA=AB
∴BC=CA=AB
例4(p54)、如图△ABC是等边三角形,DE∥BC,交AB、AC于D、E。
求证:△ADE是等边三角形相信自己:请你独立完成其证明。我能行! 议 一 议2、你认为一个等腰三角形满足什么条件时便成为等边三角形?请把你的结论与同伴交流。猜想:有一个角等于60°的等腰三角形是等边三角形吗?你能证明你的结论吗?把你的证明思路与同伴进行交流。第一种情况:当顶角是600时第二种情况:当底角是60°时已知: ⊿ABC中,AB=AC, ∠ A=600。
求证:AB=AC=BCABC证明: ⊿ABC中
∵AB=AC,
∴ ∠B=∠C (等边对等角)
∵ ∠ A=600
∴ ∠B=∠C = 600
∴AB=AC=BC第一种情况:当顶角是600时温馨提示:第二种情况,当底角是60°时,请大家课后独立完成。推论⒉ 有一个角是60°的等腰三角形是等边三角形.如图,将两个含有30°角的三角形放在一起,你能借助这个图形,找到Rt△ABC与斜边AB之间的数量关系吗?
证明 ∵△ABC与△ADC关于AC轴对称∴AB=AD且AC⊥BD又∵∠BAD=2X30°=60°∴△ABD是等边三角形又∵AB=AD,AC⊥BD∴BC=1/2AB=1/2AD定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.
三、操作思考,探索新知例5(p55) 下图是屋架设计图的一部分,点D是斜AB的中点,立柱BC、 DE垂直于横梁AC,
AB=7.4m,∠A=30°立柱BC 、 DE要多长?AB解:∵DE⊥AC, BC⊥AC, ∠A=30°得 BC=1/2AB, DE=1/2AD∴BC=1/2 ×7.4=3.7m又 AD=1/2 AB=3.7m ∴DE=1/2 AD=1/2 ×3.7=1.85m答:立柱BC的长是3.7m,DE的长是1.85m.四、范例点击 补例:等腰三角形的底角为15°,腰长为2a,求腰上的高。 已知:如图,在△ABC中,AB=AC=2a, ∠B=15 °, CD是腰AB上的高. 求CD的长。解:∵AB=AC∴∠B=∠ACB=15°∴∠DAC=30°∵CD⊥BD∴CD=1/2AC=a1、在△ABC中,AB=AC,∠C=30°,DA⊥BA于A,
BC=15,求AD的长 解:∵AB=AC∴∠B=∠C=30°∵DA⊥BA∴AD=1/2BD , ∠ADB=60°∵ ∠ADB=60° ∠C=30°∴∠DAC= ∠C=30°∴AD=DC=1/2BD∵BC=15∴AD=DC=5五、延伸拓展2、已知:如图,在等腰△ABC中,AB=AC ∠BAC=120° D为BC中点,DE⊥AB于E.证明:
∵AB=AC, ∠BAC=120°
∴∠B =30° ∵ AB=AC, D为BC中点, ∴AD⊥BC(三线合一)∵DE⊥AB∴AD=1/2AB ,∠BAD=60°等边三角形性质: 等边三角形的各角都相等,并且每一个角都等于60°.推论1:三个角都相等的三角形是等边三角形。推论⒉ 有一个角是60°的等腰三角形是等边三角形.定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.六、知识小结作业:p58 11
p58 13谢谢大家
