中心对称教学课件

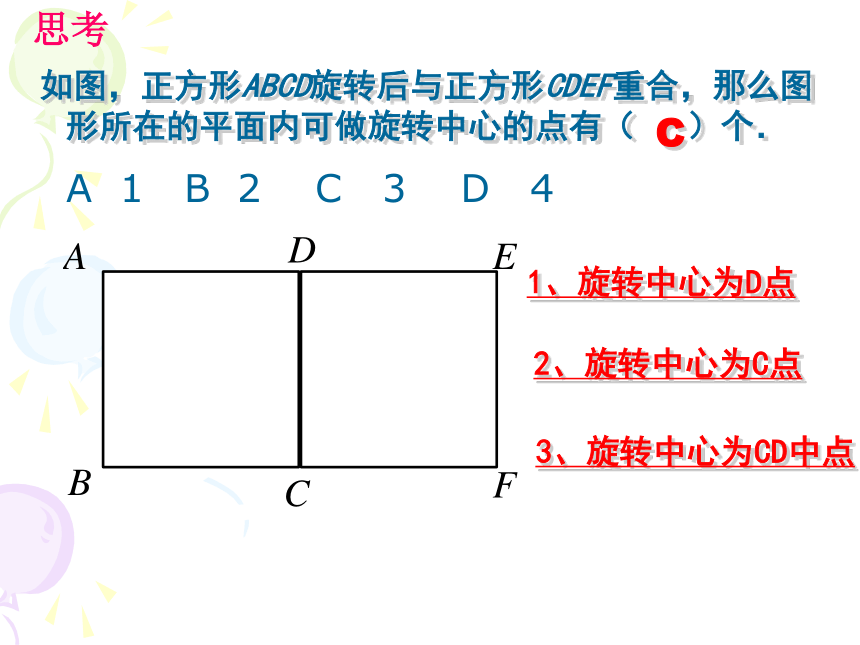
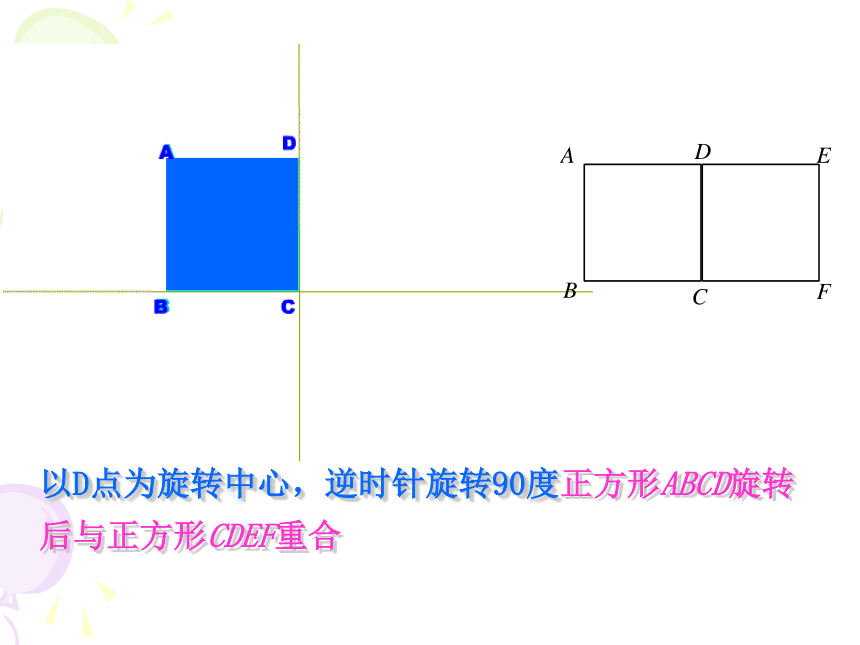
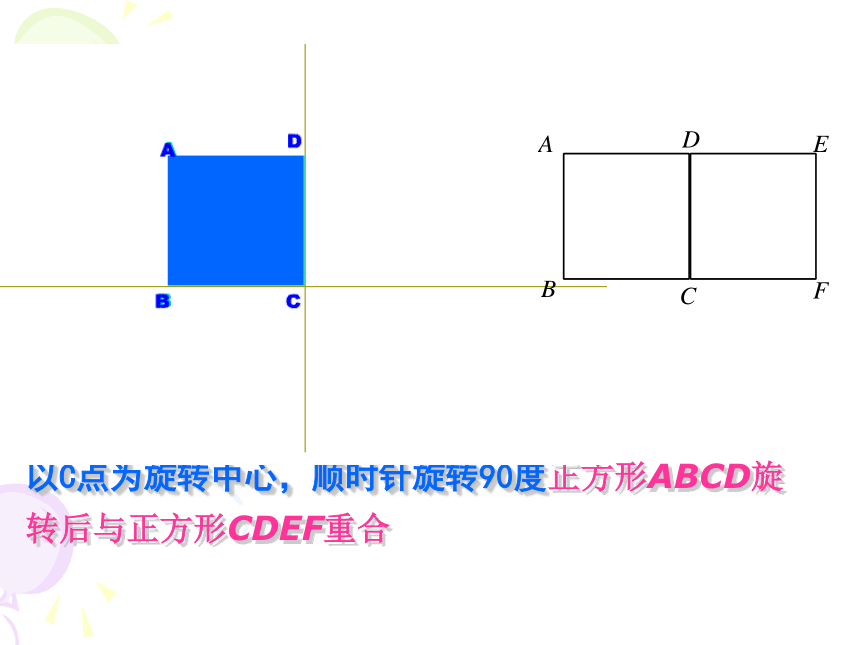
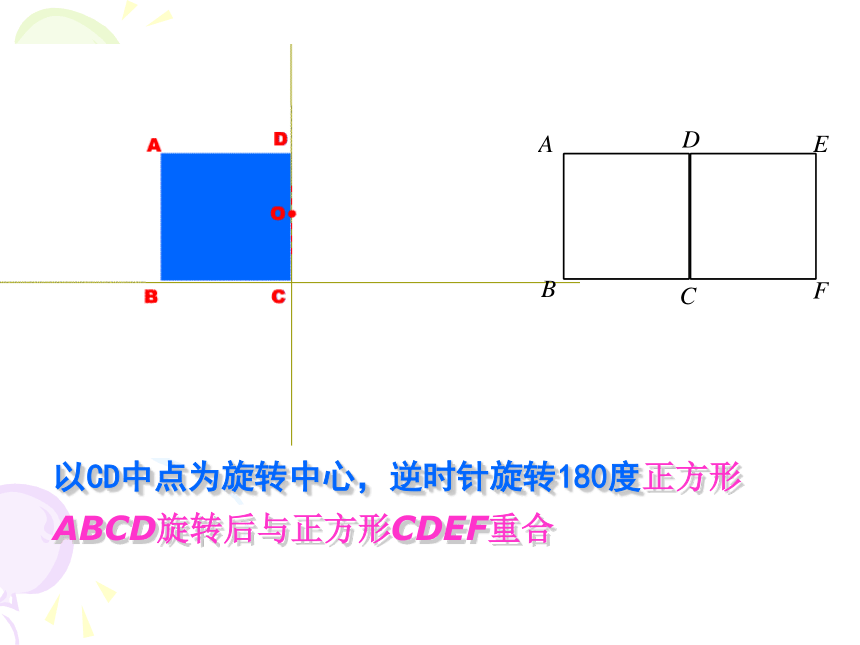
课件23张PPT。23.2.1 中心对称 同学们，看到下面的物体,你们能够回忆起什么叫旋转吗?把一个图形绕着某一点o转动一个角度的图形变换叫做旋转旋转角、旋转方向、旋转中心称为旋转三要素如图，正方形ABCD旋转后与正方形CDEF重合，那么图形所在的平面内可做旋转中心的点有（ ）个．C1、旋转中心为D点2、旋转中心为C点3、旋转中心为CD中点 A 1 B 2 C 3 D 4思考以D点为旋转中心，逆时针旋转90度正方形ABCD旋转后与正方形CDEF重合以C点为旋转中心，顺时针旋转90度正方形ABCD旋转后与正方形CDEF重合以CD中点为旋转中心，逆时针旋转180度正方形ABCD旋转后与正方形CDEF重合
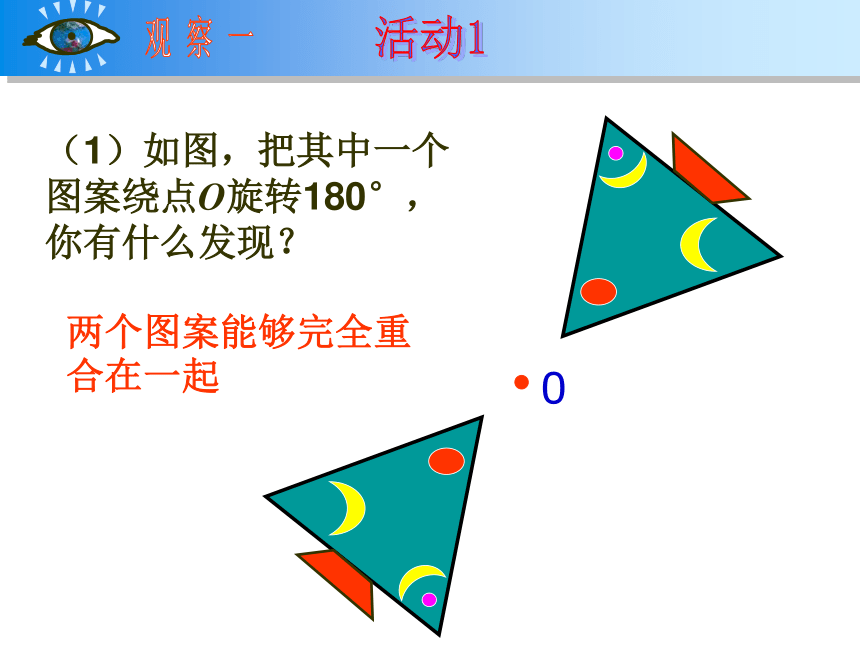
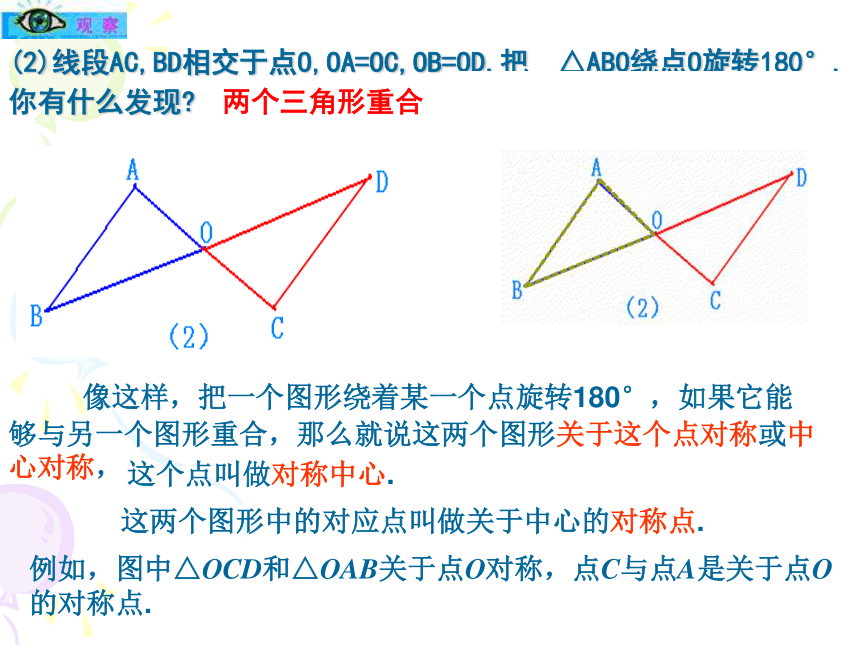
义务教育课程标准实验教材九年级23.2.1 中心对称（1）如图，把其中一个图案绕点O旋转180°，你有什么发现？观 察 一活动1两个图案能够完全重合在一起0(2)线段AC,BD相交于点O,OA=OC,OB=OD.把 △ABO绕点O旋转180°,你有什么发现? 两个三角形重合 像这样，把一个图形绕着某一个点旋转180°，如果它能够与另一个图形重合，那么就说这两个图形关于这个点对称或中心对称，例如，图中△OCD和△OAB关于点O对称，点C与点A是关于点O的对称点.这个点叫做对称中心.这两个图形中的对应点叫做关于中心的对称点. 如图，旋转三角板，画关于点O对称的两个三角形：
第一步，画出△ABC；
第二步，以三角板的一个顶点O为中心，把三角板旋转180°，画出△A′B′C′；
第三步，移开三角板.
这样画出的△ABC与△A′B′C′关于点O对称。分别连接对称点AA′、BB′、CC′.点O在线段AA′上吗？如果在，在什么位置？ △ABC与△A′B′C′有什么关系？CABC′A′B′O活动2我们可以发现：（1）点O在线段AA′上，点O是线段AA′的中点；（2）△ABC≌ △A′B′C′ （1）关于中心对称的两个图形，对称点所连线段都经过对称中心，而且被对称中心平分． （2）关于中心对称的两个图形是全等形；归 纳：中心对称轴对称观察有一个对称中心——点图形绕对称中心旋转180°后重合旋转后与另一图形重合对称点连线经过对称中心,
且被对称中心平分中心对称与轴对称有什么区别?AOA′1、以点O为对称中心,作出点A的对称点A′; 三、中心对称的作图连结OA，并延长到A’，使OA’=OA，则A’是所求的点规律总结1、画一个点关于某点(对称中心)的对称点的画
法是： 先连接这个点与对称中心，并延长一倍即可。AA′B′BO2、以点O为对称中心,作出线段AB的对称线段A′B′ 先画出图形中的几个特殊点关于某点的对称点，然后再顺次连结有关对称点即可。规律总结2、画一个图形关于某点的对称图形的画法是：
3、如图、选择点O为对称中心,画出与
△ABC关于点O对称的△A′B′C′.解:A′C′B′△A′B′C′即为所求的三角形。
4、 已知四边形ABCD和点O，画四边形A′B′C′D′，使它与已知四边形关于这一点对称。ABA’C’B’D’DOC四边形A１B１C１D１即为所求的图形。例题讲解质画一个与已知四边形ABCD中心对称图形。
（1）以顶点A为对称中心；
（2）以BC边的中点为对称中心。提高练习EFGMN 如图，已知△ABC与△A’B’C’中心对称，求出它们的对称中心O。应用解法一：根据观察，B、B’应是对应点，连结BB’，用刻度尺找出BB’的中点O，则点O即为所求（如图）O应用O解法二：根据观察，B、B’及C、C’应是两组对应点，连结BB’、CC’，BB’、CC’相交于点O，则点O即为所求（如图）。应用作业：习题23.2
谢谢！