(新人教a版选修2-1)数学:1.2《充分条件与必要条件》
文档属性
| 名称 | (新人教a版选修2-1)数学:1.2《充分条件与必要条件》 |

|
|
| 格式 | rar | ||
| 文件大小 | 135.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-13 00:00:00 | ||
图片预览





文档简介
课件24张PPT。1.2《充分条件与必要条件》教学目标 使学生正确理解充分条件、必要条件和充要条件三个概念,并能在判断、论证中正确运用.在师生、学生间的交流中增强逻辑思维活动,为用等价转化思想解决数学问题打下良好的逻辑基础.
教学重点:充分不必要条件、必要不充分条件的概念;
教学难点:判断命题的充分不必要条件、必要不充分条件;
课 型:新授课
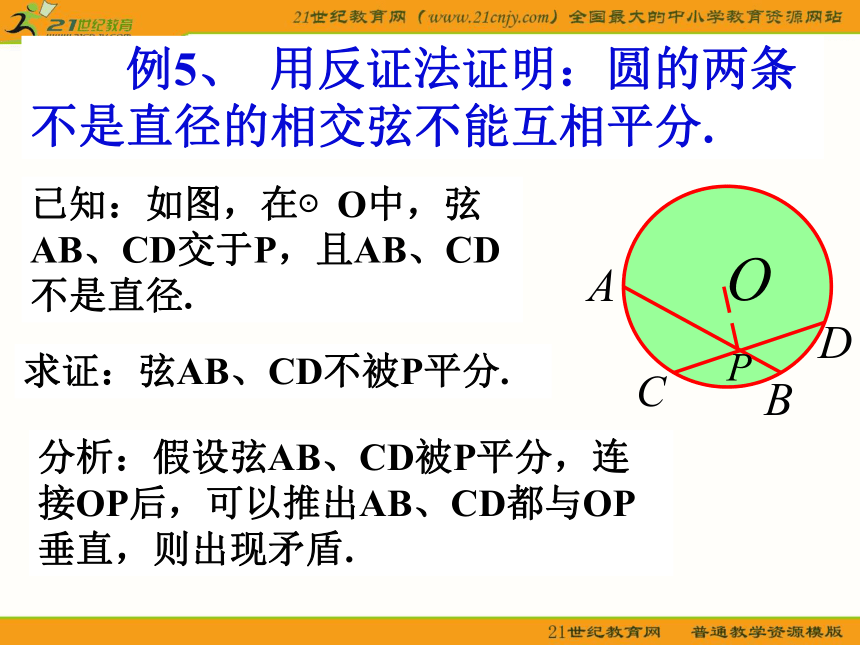
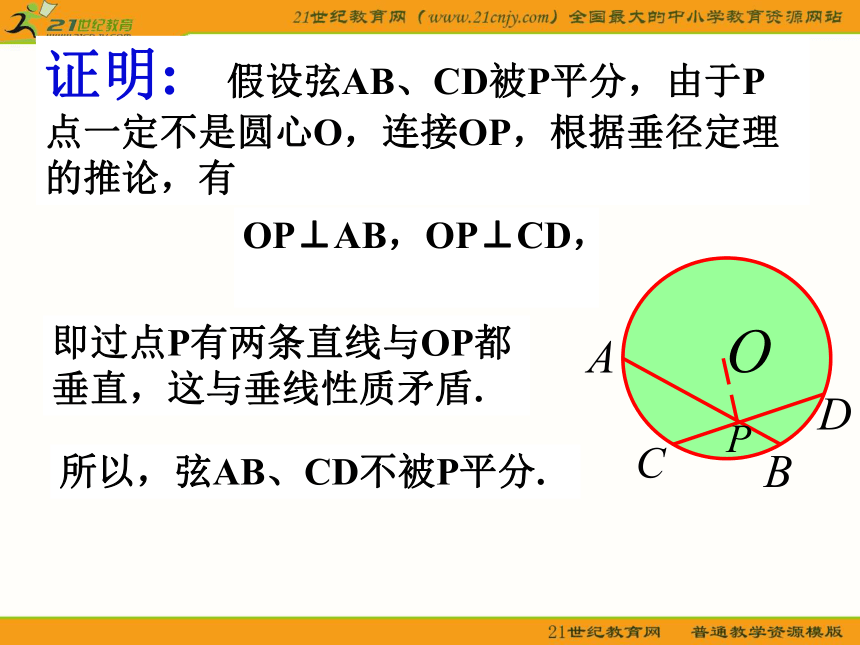
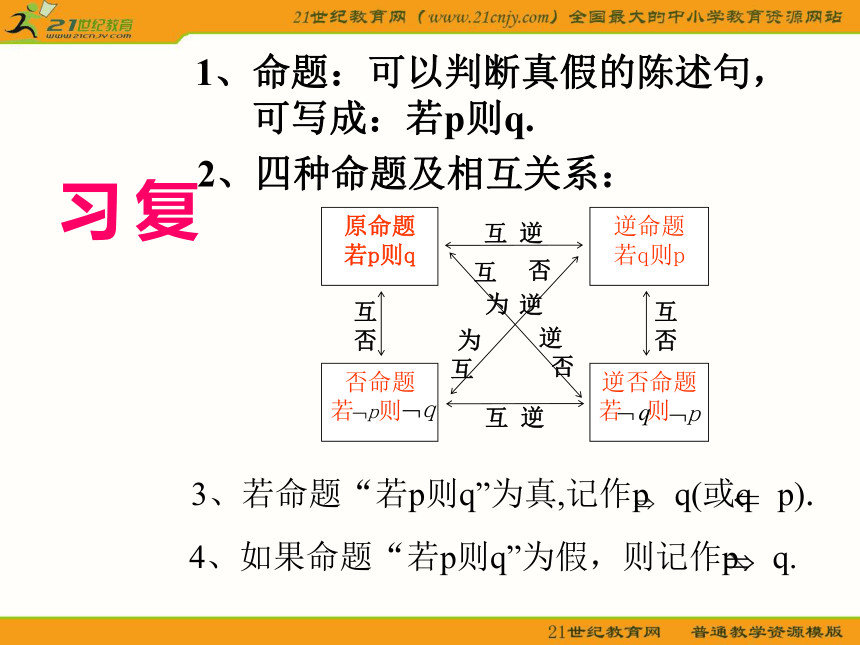
教学手段:多媒体 例5、 用反证法证明:圆的两条 不是直径的相交弦不能互相平分.已知:如图,在⊙O中,弦AB、CD交于P,且AB、CD不是直径.求证:弦AB、CD不被P平分.分析:假设弦AB、CD被P平分,连接OP后,可以推出AB、CD都与OP垂直,则出现矛盾.证明: 假设弦AB、CD被P平分,由于P点一定不是圆心O,连接OP,根据垂径定理的推论,有OP⊥AB,OP⊥CD,即过点P有两条直线与OP都垂直,这与垂线性质矛盾.所以,弦AB、CD不被P平分.思考:1.用反证法证明:若函数f(x)在区间[a,b]上是增函数,那么方程f(x)=0在区间[a,b]上至多只有一个实根.一般以下几种情况适宜使用反证法(1)结论本身是以否定形式出现的一类命题;(2)有关结论是以“至多”,或“至少”的形式出现的一类命题;(3)关于唯一性、存在性的命题;(4)结论的反面比原结论更具体、更容易研究的命题(正难则反).充分条件与必要条件 4、如果命题“若p则q”为假,则记作p q.3、若命题“若p则q”为真,记作p q(或q p).2、四种命题及相互关系:1、命题:可以判断真假的陈述句,
可写成:若p则q. 复习判断下列命题是真命题还是假命题: (1)若 ,则 ; (2)若 ,则 ; (3)对角线互相垂直的四边形是菱形; (5)若 ,则 ; (4)若方程 有两个不等的实数解,
则 . 真 假 假 假 真 (6) 若两三角形全等 ,则两三角形面积相等;
真两三角形全等 两三角形面积相等定义: 充分条件与必要条件:一般地,如果已知 ,
即命题“若p则q” 为真命题,那么就说,p 是q 的充分条件,
q 是p 的必要条件.两三角形全等是两三角形面积相等的充分条件.两三角形面积相等是两三角形全等的必要条件.两三角形全等 两三角形面积相等 例1 .指出下列各组命题中,p是q的什么条件,q是p的什么
条件.定义:对于命题“若p则q” 例2、以“充分不必要条件”、“必要不充分条件”、“充
要条件”与”既不充分也不必要条件“中选出适当的一种
填空.(充分不必要条件)(充分不必要条件)(必要不充分条件)(必要不充分条件)(充要条件)(充要条件)(既不充分也不必要条件) B A D B例7、若p是r的充分不必要条件,r是q的必要
条件,r又是s的充要条件,q是s的必要条件.
则:
1)s是p的什么条件?
2)r是q的什么条件?必要不充分条件充要条件2.充要条件的证明注意:分清p与q.①从命题角度看引申㈠若p则q是真命题,那么p是q的充分条件
q是p的必要条件.㈡若p则q是真命题,若q则p为假命题,那么p是q 的充分不必要条件,q是p必要不充分条件.(四)若p则q,若q则p都是假命题,那么p是q的既不充分也不必要条件,q是p既不充分也不必要条件.(三)若p则q,若q则p都是真命题,那么p是q的充要条件②从集合角度看
命题“若p则q”引申常用正面叙述词及它的否定. ?等于不等于小于不小于大于不大于是不是都是不都是至多有
一个至少有
两个
至少有
一个一个也
没有至多有
n个至少有
n+1个任意的某个所有的某些常用正面叙述词及它的否定. ?
教学重点:充分不必要条件、必要不充分条件的概念;
教学难点:判断命题的充分不必要条件、必要不充分条件;
课 型:新授课
教学手段:多媒体 例5、 用反证法证明:圆的两条 不是直径的相交弦不能互相平分.已知:如图,在⊙O中,弦AB、CD交于P,且AB、CD不是直径.求证:弦AB、CD不被P平分.分析:假设弦AB、CD被P平分,连接OP后,可以推出AB、CD都与OP垂直,则出现矛盾.证明: 假设弦AB、CD被P平分,由于P点一定不是圆心O,连接OP,根据垂径定理的推论,有OP⊥AB,OP⊥CD,即过点P有两条直线与OP都垂直,这与垂线性质矛盾.所以,弦AB、CD不被P平分.思考:1.用反证法证明:若函数f(x)在区间[a,b]上是增函数,那么方程f(x)=0在区间[a,b]上至多只有一个实根.一般以下几种情况适宜使用反证法(1)结论本身是以否定形式出现的一类命题;(2)有关结论是以“至多”,或“至少”的形式出现的一类命题;(3)关于唯一性、存在性的命题;(4)结论的反面比原结论更具体、更容易研究的命题(正难则反).充分条件与必要条件 4、如果命题“若p则q”为假,则记作p q.3、若命题“若p则q”为真,记作p q(或q p).2、四种命题及相互关系:1、命题:可以判断真假的陈述句,
可写成:若p则q. 复习判断下列命题是真命题还是假命题: (1)若 ,则 ; (2)若 ,则 ; (3)对角线互相垂直的四边形是菱形; (5)若 ,则 ; (4)若方程 有两个不等的实数解,
则 . 真 假 假 假 真 (6) 若两三角形全等 ,则两三角形面积相等;
真两三角形全等 两三角形面积相等定义: 充分条件与必要条件:一般地,如果已知 ,
即命题“若p则q” 为真命题,那么就说,p 是q 的充分条件,
q 是p 的必要条件.两三角形全等是两三角形面积相等的充分条件.两三角形面积相等是两三角形全等的必要条件.两三角形全等 两三角形面积相等 例1 .指出下列各组命题中,p是q的什么条件,q是p的什么
条件.定义:对于命题“若p则q” 例2、以“充分不必要条件”、“必要不充分条件”、“充
要条件”与”既不充分也不必要条件“中选出适当的一种
填空.(充分不必要条件)(充分不必要条件)(必要不充分条件)(必要不充分条件)(充要条件)(充要条件)(既不充分也不必要条件) B A D B例7、若p是r的充分不必要条件,r是q的必要
条件,r又是s的充要条件,q是s的必要条件.
则:
1)s是p的什么条件?
2)r是q的什么条件?必要不充分条件充要条件2.充要条件的证明注意:分清p与q.①从命题角度看引申㈠若p则q是真命题,那么p是q的充分条件
q是p的必要条件.㈡若p则q是真命题,若q则p为假命题,那么p是q 的充分不必要条件,q是p必要不充分条件.(四)若p则q,若q则p都是假命题,那么p是q的既不充分也不必要条件,q是p既不充分也不必要条件.(三)若p则q,若q则p都是真命题,那么p是q的充要条件②从集合角度看
命题“若p则q”引申常用正面叙述词及它的否定. ?等于不等于小于不小于大于不大于是不是都是不都是至多有
一个至少有
两个
至少有
一个一个也
没有至多有
n个至少有
n+1个任意的某个所有的某些常用正面叙述词及它的否定. ?
