(新人教a版选修2-1)数学:3.1.2《共线向量与共面向量》课件
文档属性
| 名称 | (新人教a版选修2-1)数学:3.1.2《共线向量与共面向量》课件 |  | |
| 格式 | rar | ||
| 文件大小 | 641.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-13 09:37:00 | ||
图片预览




文档简介
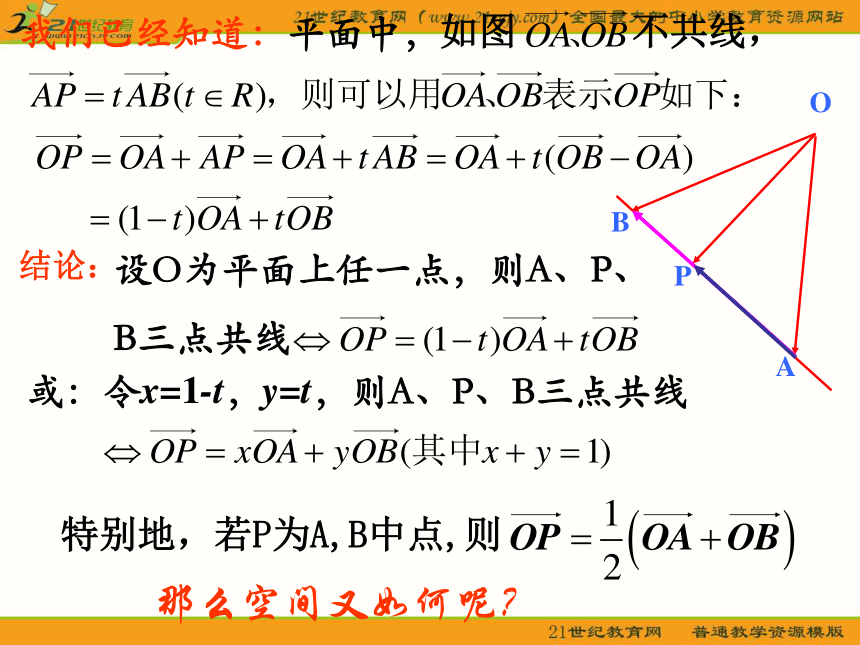
课件24张PPT。共线向量与共面向量AP特别地,若P为A,B中点,则我们已经知道:平面中,如图 不共线,结论:设O为平面上任一点,则A、P、
B三点共线或:令x=1-t,y=t,则A、P、B三点共线那么空间又如何呢?APB例1 已知A、B、P三点共线,O为直线外
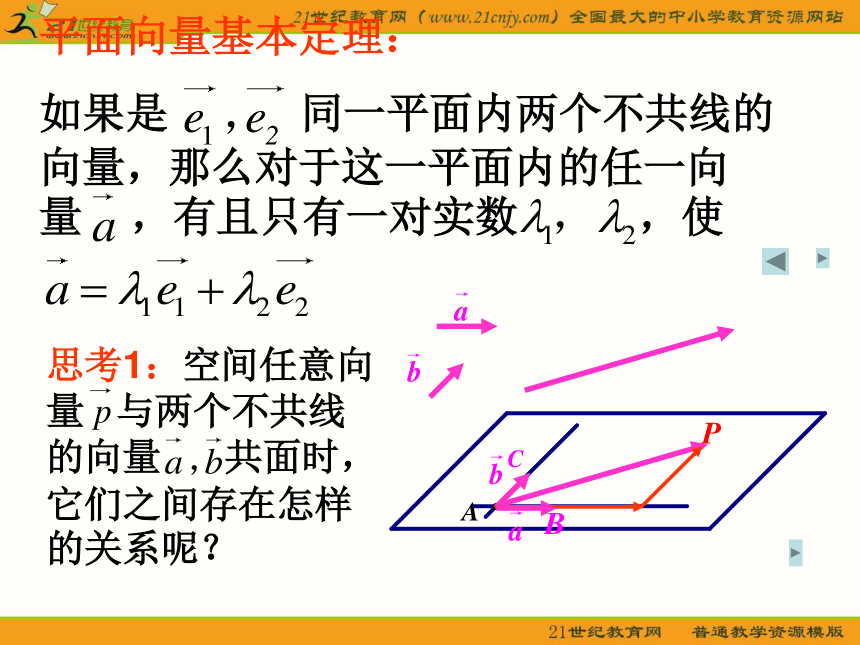
一点,且 ,求 的值. 平面向量基本定理:
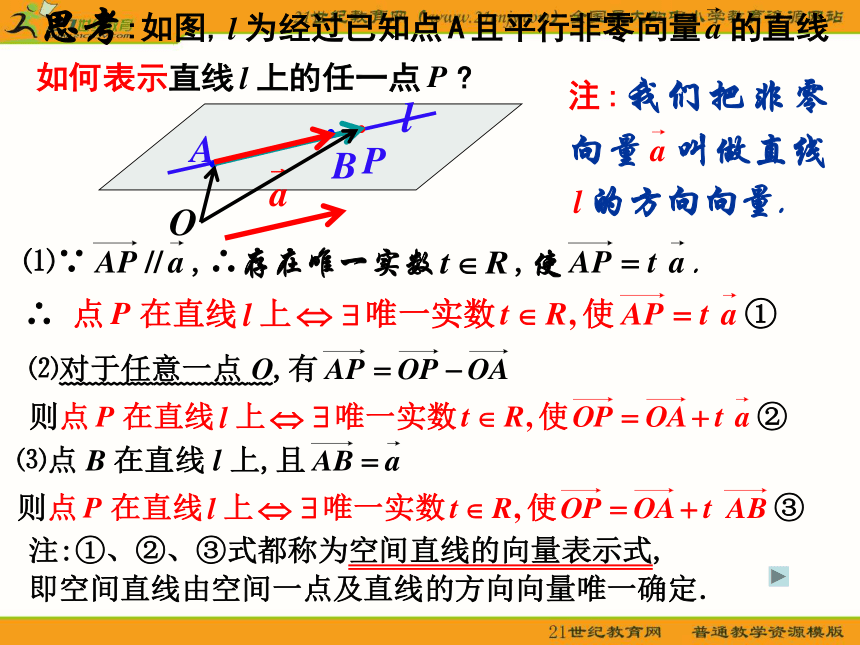
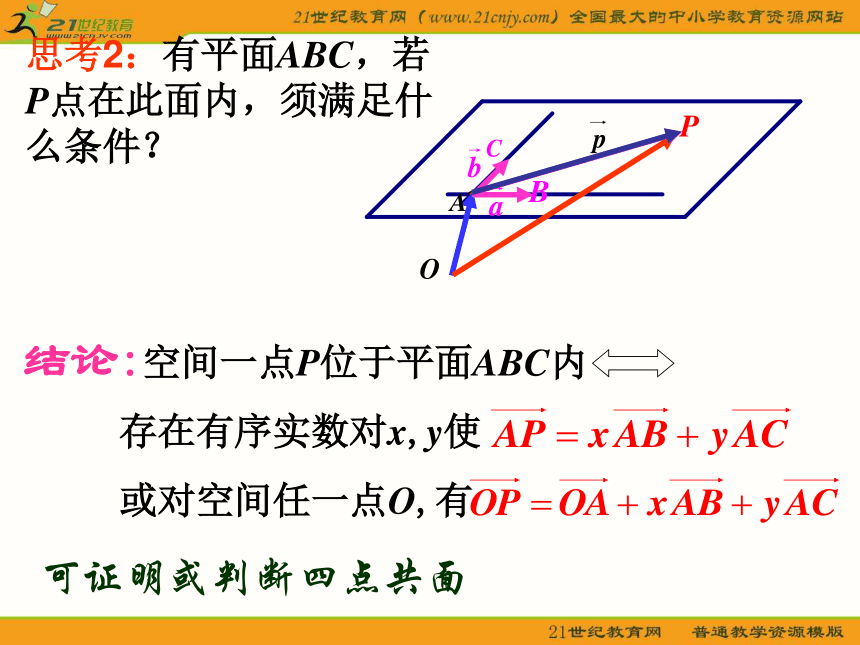
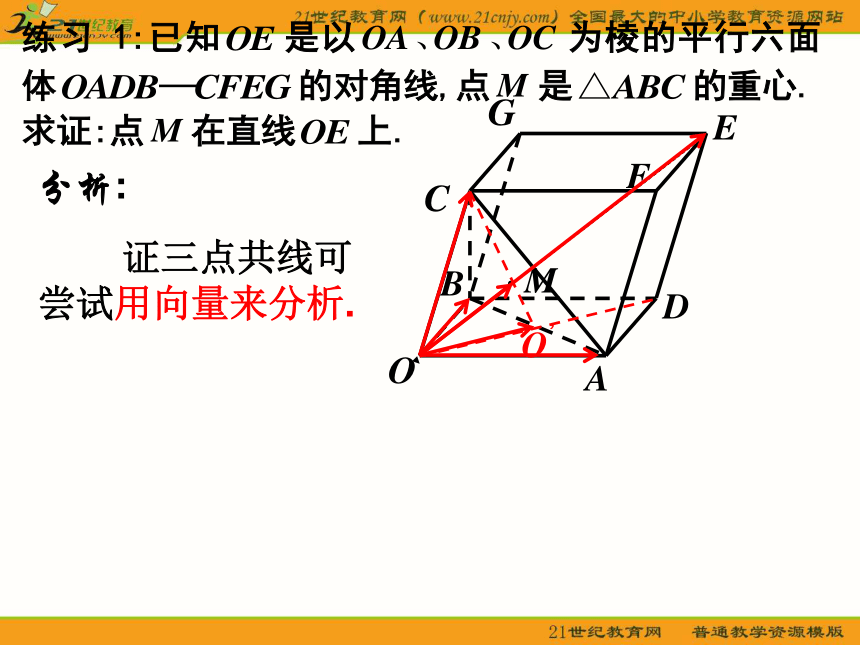
如果是 同一平面内两个不共线的向量,那么对于这一平面内的任一向量 ,有且只有一对实数 ,使思考1:空间任意向量 与两个不共线的向量 共面时,它们之间存在怎样的关系呢?二.共面向量:1.共面向量:能平移到同一平面内的向量,叫做共面向量.注意:空间任意两个向量是共面的,但空间任意三个向量就不一定共面的了。思考2:有平面ABC,若P点在此面内,须满足什么条件?可证明或判断四点共面分析:
证三点共线可尝试用向量来分析.练习2:已知矩形ABCD和ADEF所在的平面互相垂直,点M、N分别在BD,AE上,且分别是距B点、A点较近的三等分点,求证:MN//平面CDEABCDEFMN练习3: 已知A、B、M三点不共线,对于平面
ABM外的任一点O,确定在下列各条件下,
点P是否与A、B、M一定共面?类比平面向量的基本定理,在空间中应有一个什么结论?然后证唯一性证明思路:先证存在性注:空间任意三个不共面向量都可以构成空
间的一个基底.如:推论:设点O、A、B、C是不共面的四点,则对空间任一点P,都存在唯一的有序实数对 x、y、z使OABCP例1解:连AN,练习B1.对于空间任意一点O,下列命题正确的是:
(A)若 ,则P、A、B共线
(B)若 ,则P是AB的中点
(C)若 ,则P、A、B不共线
(D)若 ,则P、A、B共线2.已知点M在平面ABC内,并且对空间任意一点
O, , 则x的值为( )1.下列说明正确的是: (A)在平面内共线的向量在空间不一定共线
(B)在空间共线的向量在平面内不一定共线
(C)在平面内共线的向量在空间一定不共线
(D)在空间共线的向量在平面内一定共线2.下列说法正确的是: (A)平面内的任意两个向量都共线
(B)空间的任意三个向量都不共面
(C)空间的任意两个向量都共面
(D)空间的任意三个向量都共面补充练习:已知空间四边形OABC,对角线OB、AC,M和N分别是OA、BC的中点,点G在MN上,且使MG=2GN,试用基底 表示向量解:在△OMG中,B5.对于空间中的三个向量
它们一定是:
A.共面向量 B.共线向量
C.不共面向量
D.既不共线又不共面向量7.已知A、B、C三点不共线,对平面外一点
O,在下列条件下,点P是否与A、B、C共面?三、课堂小结:
1.共线向量的概念。
2.共线向量定理。
3.共面向量的概念。
4.共面向量定理。
B三点共线或:令x=1-t,y=t,则A、P、B三点共线那么空间又如何呢?APB例1 已知A、B、P三点共线,O为直线外
一点,且 ,求 的值. 平面向量基本定理:
如果是 同一平面内两个不共线的向量,那么对于这一平面内的任一向量 ,有且只有一对实数 ,使思考1:空间任意向量 与两个不共线的向量 共面时,它们之间存在怎样的关系呢?二.共面向量:1.共面向量:能平移到同一平面内的向量,叫做共面向量.注意:空间任意两个向量是共面的,但空间任意三个向量就不一定共面的了。思考2:有平面ABC,若P点在此面内,须满足什么条件?可证明或判断四点共面分析:
证三点共线可尝试用向量来分析.练习2:已知矩形ABCD和ADEF所在的平面互相垂直,点M、N分别在BD,AE上,且分别是距B点、A点较近的三等分点,求证:MN//平面CDEABCDEFMN练习3: 已知A、B、M三点不共线,对于平面
ABM外的任一点O,确定在下列各条件下,
点P是否与A、B、M一定共面?类比平面向量的基本定理,在空间中应有一个什么结论?然后证唯一性证明思路:先证存在性注:空间任意三个不共面向量都可以构成空
间的一个基底.如:推论:设点O、A、B、C是不共面的四点,则对空间任一点P,都存在唯一的有序实数对 x、y、z使OABCP例1解:连AN,练习B1.对于空间任意一点O,下列命题正确的是:
(A)若 ,则P、A、B共线
(B)若 ,则P是AB的中点
(C)若 ,则P、A、B不共线
(D)若 ,则P、A、B共线2.已知点M在平面ABC内,并且对空间任意一点
O, , 则x的值为( )1.下列说明正确的是: (A)在平面内共线的向量在空间不一定共线
(B)在空间共线的向量在平面内不一定共线
(C)在平面内共线的向量在空间一定不共线
(D)在空间共线的向量在平面内一定共线2.下列说法正确的是: (A)平面内的任意两个向量都共线
(B)空间的任意三个向量都不共面
(C)空间的任意两个向量都共面
(D)空间的任意三个向量都共面补充练习:已知空间四边形OABC,对角线OB、AC,M和N分别是OA、BC的中点,点G在MN上,且使MG=2GN,试用基底 表示向量解:在△OMG中,B5.对于空间中的三个向量
它们一定是:
A.共面向量 B.共线向量
C.不共面向量
D.既不共线又不共面向量7.已知A、B、C三点不共线,对平面外一点
O,在下列条件下,点P是否与A、B、C共面?三、课堂小结:
1.共线向量的概念。
2.共线向量定理。
3.共面向量的概念。
4.共面向量定理。
