(新人教a版选修2-1)数学:3.2《立体几何中的向量方法》
文档属性
| 名称 | (新人教a版选修2-1)数学:3.2《立体几何中的向量方法》 |  | |
| 格式 | rar | ||
| 文件大小 | 557.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-13 09:37:00 | ||
图片预览




文档简介
课件13张PPT。3.2《立体几何中的向量方法》教学 目标向量运算在几何证明与计算中的应用,掌握利用向量运算解几何题的方法,并能解简单的立体几何问题。
教学重点:向量运算在几何证明与计算中的应用。
教学难点:向量运算在几何证明与计算中的应用;上一节的课外思考题练习巩固引入方法的分析课外练习H 分析:面面距离转化为点面距离来求尝试:∴所求的距离是课本第114页例1的思考(3)
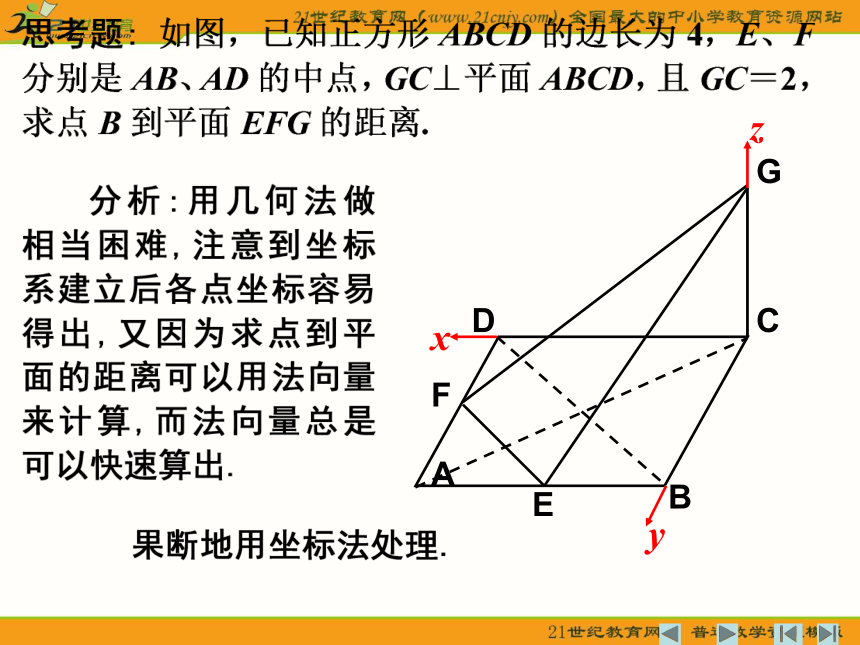
晶体中相对的两个平面之间的距离是多少?(设棱长为1) 几何法较难,如何用向量知识求点到平面的距离? 几何分析加向量运算 妙!妙!妙!能否用法向量运算求解呢?可证得如何用向量法求点到平面的距离:思考题分析DABCGFEDABCGFE2.(课本第116页练习2)如图,60°的二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直AB,已知AB=4,AC=6,BD=8,求CD的长. 解:如图,以D为原点建立空间直角坐标系D-xyz
则D(0,0,0),A( ,0,0),B( , ,0),C(0, ,0),P(0,0, )
2.如图,60°的二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直AB,已知AB=4,AC=6,BD=8,求CD的长. 例2:如图3,甲站在水库底面上的点A处,乙站在水坝斜面上的点B处。从A,B到直线 (库底与水坝的交线)的距离AC和BD分别为
和 ,CD的长为 , AB的长为 。求库底与水坝所成二面角的余弦值。 解:如图,化为向量问题根据向量的加法法则进行向量运算于是,得设向量 与 的夹角为 , 就是库底与水坝所成的二面角。因此回到图形问题库底与水坝所成二面角的余弦值为课外练习:
正三棱柱 中,D是AC的中点,当 时,求二面角 的余弦值.
CADBC1B1A1解:如图,以C为原点建立空间直角坐标系C-xyz.设底面三角形的边长为a,侧棱长为b则 C(0,0,0),故由于 ,所以 ∴ 设面 的一个法向量为
教学重点:向量运算在几何证明与计算中的应用。
教学难点:向量运算在几何证明与计算中的应用;上一节的课外思考题练习巩固引入方法的分析课外练习H 分析:面面距离转化为点面距离来求尝试:∴所求的距离是课本第114页例1的思考(3)
晶体中相对的两个平面之间的距离是多少?(设棱长为1) 几何法较难,如何用向量知识求点到平面的距离? 几何分析加向量运算 妙!妙!妙!能否用法向量运算求解呢?可证得如何用向量法求点到平面的距离:思考题分析DABCGFEDABCGFE2.(课本第116页练习2)如图,60°的二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直AB,已知AB=4,AC=6,BD=8,求CD的长. 解:如图,以D为原点建立空间直角坐标系D-xyz
则D(0,0,0),A( ,0,0),B( , ,0),C(0, ,0),P(0,0, )
2.如图,60°的二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直AB,已知AB=4,AC=6,BD=8,求CD的长. 例2:如图3,甲站在水库底面上的点A处,乙站在水坝斜面上的点B处。从A,B到直线 (库底与水坝的交线)的距离AC和BD分别为
和 ,CD的长为 , AB的长为 。求库底与水坝所成二面角的余弦值。 解:如图,化为向量问题根据向量的加法法则进行向量运算于是,得设向量 与 的夹角为 , 就是库底与水坝所成的二面角。因此回到图形问题库底与水坝所成二面角的余弦值为课外练习:
正三棱柱 中,D是AC的中点,当 时,求二面角 的余弦值.
CADBC1B1A1解:如图,以C为原点建立空间直角坐标系C-xyz.设底面三角形的边长为a,侧棱长为b则 C(0,0,0),故由于 ,所以 ∴ 设面 的一个法向量为
