(新人教a版选修2-1)数学:第十三章《空间向量与立体几何》课件
文档属性
| 名称 | (新人教a版选修2-1)数学:第十三章《空间向量与立体几何》课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 535.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-13 00:00:00 | ||
图片预览





文档简介
课件16张PPT。一、复习目标:1、理解直线的方向向量与平面的法向量并会求直线的方向向量与平面的法向量。2、理解和掌握向量共线与共面的判断方法。3、用向量法会熟练判断和证明线面平行与垂直。第十三章
《空间向量与立体几何》二、重难点:概念与方法的运用三、教学方法:探析归纳,讲练结合。
四、教学过程
(一)、知识梳理,方法定位
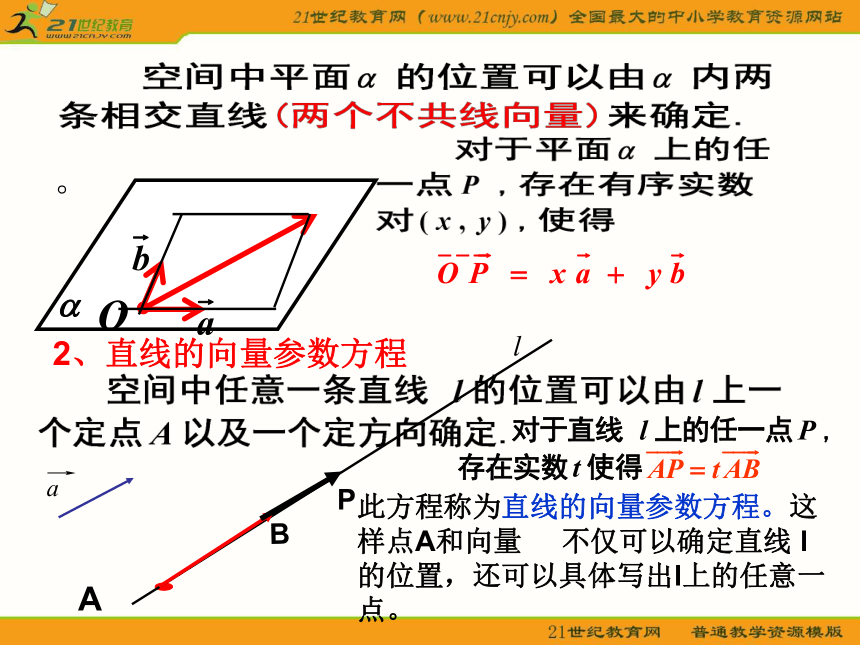
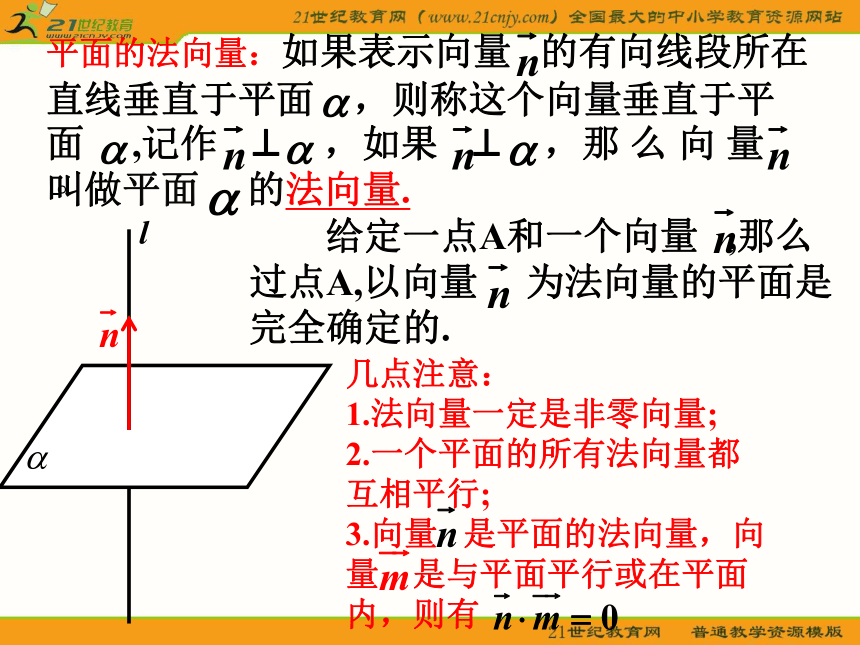
1、点、直线、平面的位置的向量表示PO。BP。2、直线的向量参数方程BP此方程称为直线的向量参数方程。这样点A和向量 不仅可以确定直线 l的位置,还可以具体写出l上的任意一点。. 3、平面的法向量P这样,点O与向量 不仅可以确定平面 的位置,还可以具体表示出 内的任意一点。除 此之外, 还可以用垂直于平面的直线的方向向量(这个平面的法向量)表示空间中平面的位置. 。平面的法向量:如果表示向量 的有向线段所在直线垂直于平面 ,则称这个向量垂直于平面 ,记作 ⊥ ,如果 ⊥ ,那 么 向 量 叫做平面 的法向量. 给定一点A和一个向量 ,那么过点A,以向量 为法向量的平面是完全确定的.几点注意:
1.法向量一定是非零向量;
2.一个平面的所有法向量都互相平行;
3.向量 是平面的法向量,向量 是与平面平行或在平面内,则有步骤:求法:4、用方向向量和法向量判定位置关系..(二)例题探析
例1、用向量法证明:一条直线与一个平面内两条相交直线都垂直,则该直线与此平面垂直。已知:直线m,n是平面 内的任意两条相交直线,且。例2、已知点 是平行四边形 所在平面外一点,如果 , ,
(1)求证: 是平面 的法向量;
(2)求平行四边形 的面积.
(1)证明:∵ ,
,
∴ , ,又 , 平面 ,
∴ 是平面 的法向量.
∴.。。例3:如图在四棱锥P—ABCD中底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F。
(1)求证PA∥平面EDB
(2)求证PB⊥平面EFD
(3)求二面角C---PB---D的大小.解:如图建立空间直角坐标系,点D为坐标原点,设DC=1.(1)证明:连结AC,AC交BD于点G,连结EG依题意得A(1,0,0)P(0,0,1)E(因为底面ABCD是正方形,所以点G是此正方形的中心,
故点G的坐标为( )且), ,,所以而EG平面EDB,且PA平面EDB,因此PA//平面EDB。(2)证明;依题意得
B(1,1,0) ,故所以由已知所以 (3)解:已知 由(2)可知 ,故 是二面角C-PB-D的平面角。 设点F的坐标为( ),则 ,因为 所以 , 因为 所以 所以 ,点F的坐标为 ,又点E的 坐标为 所以 因为 所以 即二面角C-PB-D的大小为 。。 (三)、强化巩固训练 1、设直线l,m的方向向量分别为 , ,根据下列条件判断l,m的位置关系: .2、设平面 , 的法向量分别为 , ,根据下列条件判断 , 的位置关系: 3、棱长为a的正方体ABCD—A1B1C1D1中,在棱DD1上是否存在点P使B1D⊥面PAC? 解:以D为原点建立如图所示的坐标系, 设存在点P(0,0,z), =(-a,0,z), =(-a,a,0), =(a,a,a), ∵B1D⊥面PAC,∴ , ∴-a2+az=0∴z=a,即点P与D1重合 ∴点P与D1重合时,DB1⊥面PAC。(四)、小结:本课主要探析了1、直线的方向向量与平面的法向量 的概念与求法;2、用方向向量和法向量判定线面位置关系的方法。要求大家理解和掌握并会熟练运用。
(五)、作业布置:复资P132中2、4、5、6题。五、教学反思
《空间向量与立体几何》二、重难点:概念与方法的运用三、教学方法:探析归纳,讲练结合。
四、教学过程
(一)、知识梳理,方法定位
1、点、直线、平面的位置的向量表示PO。BP。2、直线的向量参数方程BP此方程称为直线的向量参数方程。这样点A和向量 不仅可以确定直线 l的位置,还可以具体写出l上的任意一点。. 3、平面的法向量P这样,点O与向量 不仅可以确定平面 的位置,还可以具体表示出 内的任意一点。除 此之外, 还可以用垂直于平面的直线的方向向量(这个平面的法向量)表示空间中平面的位置. 。平面的法向量:如果表示向量 的有向线段所在直线垂直于平面 ,则称这个向量垂直于平面 ,记作 ⊥ ,如果 ⊥ ,那 么 向 量 叫做平面 的法向量. 给定一点A和一个向量 ,那么过点A,以向量 为法向量的平面是完全确定的.几点注意:
1.法向量一定是非零向量;
2.一个平面的所有法向量都互相平行;
3.向量 是平面的法向量,向量 是与平面平行或在平面内,则有步骤:求法:4、用方向向量和法向量判定位置关系..(二)例题探析
例1、用向量法证明:一条直线与一个平面内两条相交直线都垂直,则该直线与此平面垂直。已知:直线m,n是平面 内的任意两条相交直线,且。例2、已知点 是平行四边形 所在平面外一点,如果 , ,
(1)求证: 是平面 的法向量;
(2)求平行四边形 的面积.
(1)证明:∵ ,
,
∴ , ,又 , 平面 ,
∴ 是平面 的法向量.
∴.。。例3:如图在四棱锥P—ABCD中底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F。
(1)求证PA∥平面EDB
(2)求证PB⊥平面EFD
(3)求二面角C---PB---D的大小.解:如图建立空间直角坐标系,点D为坐标原点,设DC=1.(1)证明:连结AC,AC交BD于点G,连结EG依题意得A(1,0,0)P(0,0,1)E(因为底面ABCD是正方形,所以点G是此正方形的中心,
故点G的坐标为( )且), ,,所以而EG平面EDB,且PA平面EDB,因此PA//平面EDB。(2)证明;依题意得
B(1,1,0) ,故所以由已知所以 (3)解:已知 由(2)可知 ,故 是二面角C-PB-D的平面角。 设点F的坐标为( ),则 ,因为 所以 , 因为 所以 所以 ,点F的坐标为 ,又点E的 坐标为 所以 因为 所以 即二面角C-PB-D的大小为 。。 (三)、强化巩固训练 1、设直线l,m的方向向量分别为 , ,根据下列条件判断l,m的位置关系: .2、设平面 , 的法向量分别为 , ,根据下列条件判断 , 的位置关系: 3、棱长为a的正方体ABCD—A1B1C1D1中,在棱DD1上是否存在点P使B1D⊥面PAC? 解:以D为原点建立如图所示的坐标系, 设存在点P(0,0,z), =(-a,0,z), =(-a,a,0), =(a,a,a), ∵B1D⊥面PAC,∴ , ∴-a2+az=0∴z=a,即点P与D1重合 ∴点P与D1重合时,DB1⊥面PAC。(四)、小结:本课主要探析了1、直线的方向向量与平面的法向量 的概念与求法;2、用方向向量和法向量判定线面位置关系的方法。要求大家理解和掌握并会熟练运用。
(五)、作业布置:复资P132中2、4、5、6题。五、教学反思
