(苏教版选修1—2)数学:4.1流程图(课件)
文档属性
| 名称 | (苏教版选修1—2)数学:4.1流程图(课件) |

|
|
| 格式 | rar | ||
| 文件大小 | 55.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-13 00:00:00 | ||
图片预览



文档简介
课件13张PPT。结构图
流程图框图 程序框图
工序流程图
数学中的流程图
其它流程图用程序解决问题的步骤:
1、分析问题
2、设计算法
3、编制程序
4、调试运行第一步:用自然语言描述算法
第二步:画出程序框图表示算法比较:用程序框图表达的算法比用自然语言描 述的算法步骤更直观、明确、清楚,而且更容易 转化为计算机程序。三种基本的逻辑结构
1、顺序结构
2、条件结构(选择结构)
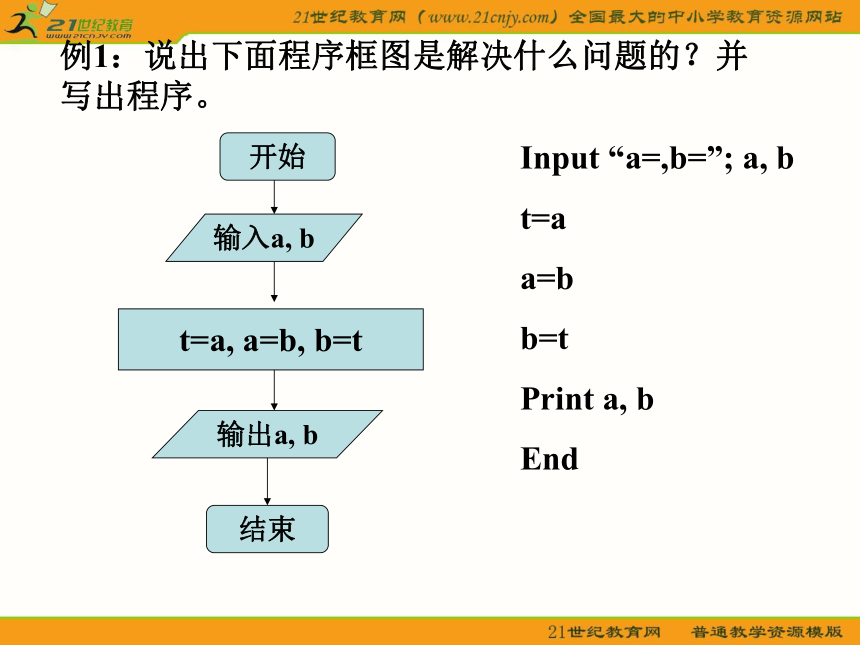
3、循环结构例1:说出下面程序框图是解决什么问题的?并写出程序。Input “a=,b=”; a, b
t=a
a=b
b=t
Print a, b
End
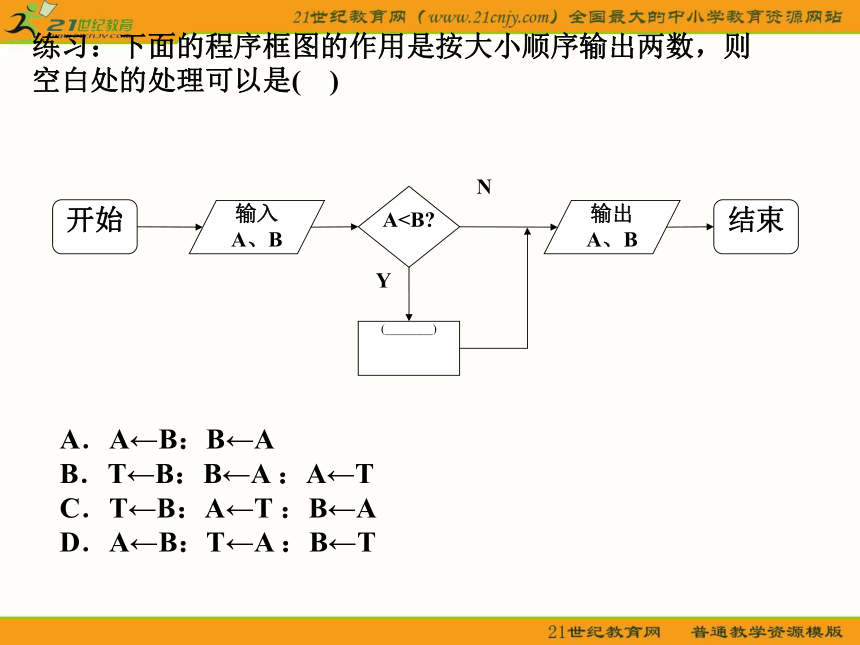
练习:下面的程序框图的作用是按大小顺序输出两数,则空白处的处理可以是( ) A.A←B:B←A
B.T←B:B←A :A←T
C.T←B:A←T :B←A
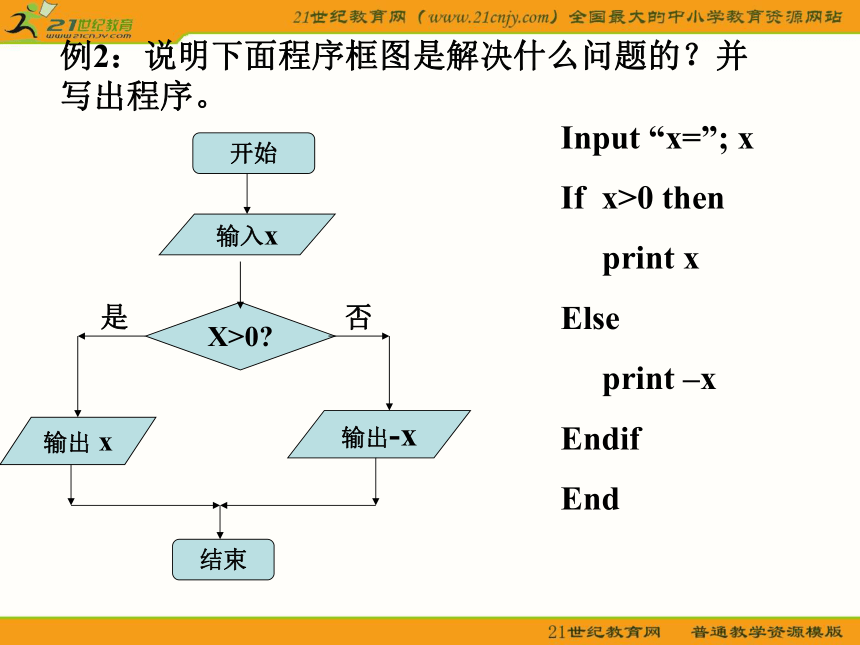
D.A←B:T←A :B←T例2:说明下面程序框图是解决什么问题的?并写出程序。Input “x=”; x
If x>0 then
print x
Else
print –x
Endif
End
否是例3: P74 练习1
算法:
1、令sun=0, i=1
2、令sum=sum+i ,
i=i+1,
sum=sum-i,
i=i+1
3、判断 i≤100吗?
是,进行第二步;
否,输出sum。
开始i=1, sum=0sum=sum+ii=i+1sum=sum-i, i=i+1i≤100?输出sum结束否是开始i=1, sum=0sum=sum+(-1)i-1×ii=i+1i≤100?输出sum结束否是练习:
说出左边程序框图的功能。开始输入x x<5?y=2x2+2y=x2-1输出S 结束例4:这是一个算法的流程图,当输入的值为3时,输出的结果为多少? 例5:有如下程序框图,表示的算法的功能是什么? 例6:阅读流程图,解答下列问题:
(1)变量y在这个算法中的作用是什么?
(2)这个算法的循环体是哪一部分?功能是什么?
(3)这个算法的处理功能是什么?例7 画出用二分法求方程x2-2=0的近似根的程序框图。算法:
1、令f(x)=x2-2,误差为ε,因为 f(1)<0 , f(2)>0 ,所 以设 x1=1,x2=2。
2、令m=(x1+x2)/2 ,判断f(m)是否为0。若是,则m为方程的根,若否,则判断f(x1)·f(m)的符号。
3、若 f(x1)·f(m)>0,则令x1=m ;否则,令x2=m。
4、判断|x1-x2|<ε是否成立?成立,则 m为方程的近似根,若不成立,同返回第二步。F(x)=x2-2输入ε,x1,x2的值m=(x1+x2)/2f(m)=0?f(x1) · f(m)>0?X1=mX2=m|x1-x2|<ε输出m输出m是否是否是否
流程图框图 程序框图
工序流程图
数学中的流程图
其它流程图用程序解决问题的步骤:
1、分析问题
2、设计算法
3、编制程序
4、调试运行第一步:用自然语言描述算法
第二步:画出程序框图表示算法比较:用程序框图表达的算法比用自然语言描 述的算法步骤更直观、明确、清楚,而且更容易 转化为计算机程序。三种基本的逻辑结构
1、顺序结构
2、条件结构(选择结构)
3、循环结构例1:说出下面程序框图是解决什么问题的?并写出程序。Input “a=,b=”; a, b
t=a
a=b
b=t
Print a, b
End
练习:下面的程序框图的作用是按大小顺序输出两数,则空白处的处理可以是( ) A.A←B:B←A
B.T←B:B←A :A←T
C.T←B:A←T :B←A
D.A←B:T←A :B←T例2:说明下面程序框图是解决什么问题的?并写出程序。Input “x=”; x
If x>0 then
print x
Else
print –x
Endif
End
否是例3: P74 练习1
算法:
1、令sun=0, i=1
2、令sum=sum+i ,
i=i+1,
sum=sum-i,
i=i+1
3、判断 i≤100吗?
是,进行第二步;
否,输出sum。
开始i=1, sum=0sum=sum+ii=i+1sum=sum-i, i=i+1i≤100?输出sum结束否是开始i=1, sum=0sum=sum+(-1)i-1×ii=i+1i≤100?输出sum结束否是练习:
说出左边程序框图的功能。开始输入x x<5?y=2x2+2y=x2-1输出S 结束例4:这是一个算法的流程图,当输入的值为3时,输出的结果为多少? 例5:有如下程序框图,表示的算法的功能是什么? 例6:阅读流程图,解答下列问题:
(1)变量y在这个算法中的作用是什么?
(2)这个算法的循环体是哪一部分?功能是什么?
(3)这个算法的处理功能是什么?例7 画出用二分法求方程x2-2=0的近似根的程序框图。算法:
1、令f(x)=x2-2,误差为ε,因为 f(1)<0 , f(2)>0 ,所 以设 x1=1,x2=2。
2、令m=(x1+x2)/2 ,判断f(m)是否为0。若是,则m为方程的根,若否,则判断f(x1)·f(m)的符号。
3、若 f(x1)·f(m)>0,则令x1=m ;否则,令x2=m。
4、判断|x1-x2|<ε是否成立?成立,则 m为方程的近似根,若不成立,同返回第二步。F(x)=x2-2输入ε,x1,x2的值m=(x1+x2)/2f(m)=0?f(x1) · f(m)>0?X1=mX2=m|x1-x2|<ε输出m输出m是否是否是否
