2011年中考数学专题复习教学案--动手操作题(附答案)
文档属性
| 名称 | 2011年中考数学专题复习教学案--动手操作题(附答案) |  | |
| 格式 | rar | ||
| 文件大小 | 905.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-13 16:54:00 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
动手操作题
近年来中考数学试题加强了对学生动手操作能力的考查,出现了一类新题型--动手操作题.这类试题能够有效地考查学生的实践能力、创新意识和直觉思维能力.解决这类问题需要通过观察、操作、比较、猜想、分析、综合、抽象和概括等实践活动和思维过程,灵活运用所学知识和生活经验,探索和发现结论,从而解决问题.
中考数学试题中动手操作题可分为图形折叠型动手操作题、图形拼接型动手操作题、图形分割型动手操作题和作图型动手操作题等四种类型.
类型一:图形折叠型动手操作题
图形折叠型动手操作题,就是通过图形的折叠来研究它的相关结论.
例1 (2009·河南)动手操作:在矩形纸片ABCD中,AB=3,AD=5.如图1所示,折叠纸片,使点A落在BC边上的A’处,折痕为PQ,当点A’在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点A’在BC边上可移动的最大距离为 .
【分析与解答】(1)当P点与B点重合时,此时A’点离B点最远(如图2),且.
(2)Q点与D点重合时,此时A’点离B点最近(如图3).设,则,又因为,在中,由勾股定理,得,解得,(舍去).即.
综合(1)、(2)可知,A’点在BC边上可移动的最大距离为.
同步测试1
(2009·河北)如图4,等边△ABC的边长为1 cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点 处,且点在△ABC外部,则阴影部分图形的周长为 cm.
【答案】1.
类型二:图形拼接型动手操作题
图形拼接问题,就是将已知的若干个图形重新拼合成符合条件的新图形.
例2 (2009·安徽)如图5,将正方形沿图中虚线(其中x<y)剪成①②③④四块图形,用这四块图形恰能拼成一个矩形(非正方形).请画出拼成的矩形的简图.
【分析与解答】我们观察图5中的4块图形各边之间的对应关系,找出能拼接在一起的边,如图6就是一种拼接方法.
同步测试2
(2008·襄樊)如图7是一个等腰直角三角形纸片,按图中裁剪线将这个纸片裁剪成三部分.请你将这三部分小纸片重新分别拼接成:(1)一个非矩形的平行四边形;(2)一个等腰梯形;(3)一个正方形.请画出拼接后的三个图形.
【答案】拼接后的平行四边形、等腰梯形和正方形如图8:
类型三:图形分割型动手操作题
图形分割型动手操作题就是按照要求把一个图形先分割成若干块,然后再把它们拼合一个符合条件的图形.
例3(2009·浙江义乌)(1)如图9,正方形网格中有一个平行四边形,请在图9中画一条直线把平行四边形分成面积相等的两部分;(2)把图10中的平行四边形分割成四个全等的四边形(要求在图10中画出分割线),并把所得的四个全等的四边形在图11中拼成一个轴对称图形或中心对称图形,使所得图形与原图形不全等且各个顶点都落在格点上.
图9 图10 图11
【分析与解答】本题让我们根据题目的要求先把平行四边形分割成几部分,然后再用分割的图形拼合出对称的图案来.
(1)把平行四边形分成面积相等的两部分,只要这条直线经过平行四边形的对称中心就可以.图略.
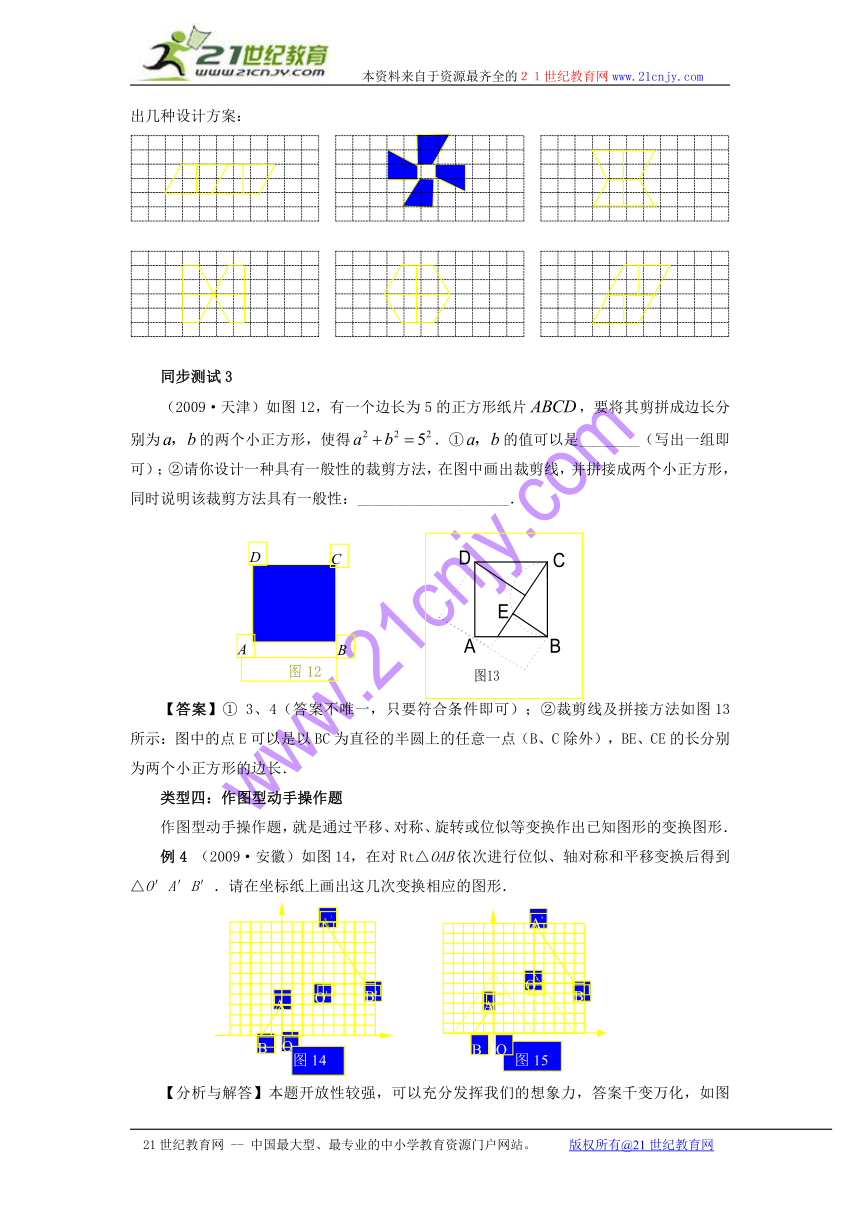
(1)此问题具有一定的开放性,解决问题的方案有多种,只要符合要求即可.下面给出几种设计方案:
同步测试3
(2009·天津)如图12,有一个边长为5的正方形纸片,要将其剪拼成边长分别为的两个小正方形,使得.①的值可以是________(写出一组即可);②请你设计一种具有一般性的裁剪方法,在图中画出裁剪线,并拼接成两个小正方形,同时说明该裁剪方法具有一般性:____________________.
【答案】① 3、4(答案不唯一,只要符合条件即可);②裁剪线及拼接方法如图13所示:图中的点E可以是以BC为直径的半圆上的任意一点(B、C除外),BE、CE的长分别为两个小正方形的边长.
类型四:作图型动手操作题
作图型动手操作题,就是通过平移、对称、旋转或位似等变换作出已知图形的变换图形.
例4 (2009·安徽)如图14,在对Rt△OAB依次进行位似、轴对称和平移变换后得到△O′A′B′.请在坐标纸上画出这几次变换相应的图形.
【分析与解答】本题开放性较强,可以充分发挥我们的想象力,答案千变万化,如图15就是一种作图方案:以O为位似中心把Rt△OAB放大2倍→沿y轴翻折→向右平移4个单位→向上平移5个单位.
同步测试4
(2009·南宁)已知在平面直角坐标系中的位置如图16所示.画出绕点按顺时针方向旋转.
【答案】旋转后的图形如图17.
随堂检测
1. 如图18所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠EFB=65°,则∠AED′等于 ( )
(A) 70°
(B) 65°
(C) 50°
(D) 25°
2. 如图19,将三角形纸片ABC沿EF折叠可得图20(其中EF∥BC),已知图20的图形面积与原三角形的面积之比为3∶4,且阴影部分的面积为8,则原三角形面积为( ).
A.32 B.16 C.20 D.12
3. 把长为8cm的矩形按虚线对折,按图21中的虚线剪出一个直角梯形,打开得到一个等腰梯形,剪掉部分的面积为6cm2,则打开后梯形的周长是( )
A.(10+2)cm B.(10+)cm C.22cm D.18cm
4.图22-1是两个由同样大的小方格组成的图形,我们可以用不同的方法把这两个图形拼成一个轴对称图形,例如图22-2就是这样的轴对称图形,沿某条直线折叠后,直线两侧的图形能够完全重合.请问:符合要求的拼法一共有 种.
5.将任意三角形剪切可以拼成一个与此三角形面积相等的矩形.
方法如下(如图23—1):
请你类似上面图示的方法,解答下列的问题:
(1)对任意三角形(如图23—2),设计一种与上例不同的方案,将它分成若干块,再拼成一个与原三角形面积相等的矩形.
(2)对任意四边形(如图23—3),设计一种方案,将它分成若干块,再拼成一个与原四边形面积相等的矩形.
6.如图所示,左边方格纸中每个正方形的边长均为a,右边方格纸中每个正方形的边长均为b,将左边方格纸中的图形顺时针旋转90°,并按b:a的比例画在右边方格纸中.
随堂检测答案:
1.C ;2.D ;3.A ;4.3 ;
5.(1)
(2)
6.画图如下:
A
B
C
图4
D
E
A′
图12
D
C
B
A
A'
B'
O'
A
B
O
′
图14
图15
O'
A'
B'
A
O
′
′
B
y
x
8
7
6
5
4
3
2
1
0
8
7
6
5
4
3
2
1
B
C
A
图16
y
x
8
7
6
5
4
3
2
1
0
8
7
6
5
4
3
2
1
B
C
A
图17
E
D
B
C′
F
C
D′
A
图18
图19
图20
图21
②
图23—1
①
③
②
③
①
中点
中点
图23—2
图23—3
②
中点
中点
①
③
②
①
③
③
①
②
④
⑤
⑥
①
③
②
④
⑥
⑤
中点
中点
中点
中点
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
动手操作题
近年来中考数学试题加强了对学生动手操作能力的考查,出现了一类新题型--动手操作题.这类试题能够有效地考查学生的实践能力、创新意识和直觉思维能力.解决这类问题需要通过观察、操作、比较、猜想、分析、综合、抽象和概括等实践活动和思维过程,灵活运用所学知识和生活经验,探索和发现结论,从而解决问题.
中考数学试题中动手操作题可分为图形折叠型动手操作题、图形拼接型动手操作题、图形分割型动手操作题和作图型动手操作题等四种类型.
类型一:图形折叠型动手操作题
图形折叠型动手操作题,就是通过图形的折叠来研究它的相关结论.
例1 (2009·河南)动手操作:在矩形纸片ABCD中,AB=3,AD=5.如图1所示,折叠纸片,使点A落在BC边上的A’处,折痕为PQ,当点A’在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P、Q分别在AB、AD边上移动,则点A’在BC边上可移动的最大距离为 .
【分析与解答】(1)当P点与B点重合时,此时A’点离B点最远(如图2),且.
(2)Q点与D点重合时,此时A’点离B点最近(如图3).设,则,又因为,在中,由勾股定理,得,解得,(舍去).即.
综合(1)、(2)可知,A’点在BC边上可移动的最大距离为.
同步测试1
(2009·河北)如图4,等边△ABC的边长为1 cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点 处,且点在△ABC外部,则阴影部分图形的周长为 cm.
【答案】1.
类型二:图形拼接型动手操作题
图形拼接问题,就是将已知的若干个图形重新拼合成符合条件的新图形.
例2 (2009·安徽)如图5,将正方形沿图中虚线(其中x<y)剪成①②③④四块图形,用这四块图形恰能拼成一个矩形(非正方形).请画出拼成的矩形的简图.
【分析与解答】我们观察图5中的4块图形各边之间的对应关系,找出能拼接在一起的边,如图6就是一种拼接方法.
同步测试2
(2008·襄樊)如图7是一个等腰直角三角形纸片,按图中裁剪线将这个纸片裁剪成三部分.请你将这三部分小纸片重新分别拼接成:(1)一个非矩形的平行四边形;(2)一个等腰梯形;(3)一个正方形.请画出拼接后的三个图形.
【答案】拼接后的平行四边形、等腰梯形和正方形如图8:
类型三:图形分割型动手操作题
图形分割型动手操作题就是按照要求把一个图形先分割成若干块,然后再把它们拼合一个符合条件的图形.
例3(2009·浙江义乌)(1)如图9,正方形网格中有一个平行四边形,请在图9中画一条直线把平行四边形分成面积相等的两部分;(2)把图10中的平行四边形分割成四个全等的四边形(要求在图10中画出分割线),并把所得的四个全等的四边形在图11中拼成一个轴对称图形或中心对称图形,使所得图形与原图形不全等且各个顶点都落在格点上.
图9 图10 图11
【分析与解答】本题让我们根据题目的要求先把平行四边形分割成几部分,然后再用分割的图形拼合出对称的图案来.
(1)把平行四边形分成面积相等的两部分,只要这条直线经过平行四边形的对称中心就可以.图略.
(1)此问题具有一定的开放性,解决问题的方案有多种,只要符合要求即可.下面给出几种设计方案:
同步测试3
(2009·天津)如图12,有一个边长为5的正方形纸片,要将其剪拼成边长分别为的两个小正方形,使得.①的值可以是________(写出一组即可);②请你设计一种具有一般性的裁剪方法,在图中画出裁剪线,并拼接成两个小正方形,同时说明该裁剪方法具有一般性:____________________.
【答案】① 3、4(答案不唯一,只要符合条件即可);②裁剪线及拼接方法如图13所示:图中的点E可以是以BC为直径的半圆上的任意一点(B、C除外),BE、CE的长分别为两个小正方形的边长.
类型四:作图型动手操作题
作图型动手操作题,就是通过平移、对称、旋转或位似等变换作出已知图形的变换图形.
例4 (2009·安徽)如图14,在对Rt△OAB依次进行位似、轴对称和平移变换后得到△O′A′B′.请在坐标纸上画出这几次变换相应的图形.
【分析与解答】本题开放性较强,可以充分发挥我们的想象力,答案千变万化,如图15就是一种作图方案:以O为位似中心把Rt△OAB放大2倍→沿y轴翻折→向右平移4个单位→向上平移5个单位.
同步测试4
(2009·南宁)已知在平面直角坐标系中的位置如图16所示.画出绕点按顺时针方向旋转.
【答案】旋转后的图形如图17.
随堂检测
1. 如图18所示,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠EFB=65°,则∠AED′等于 ( )
(A) 70°
(B) 65°
(C) 50°
(D) 25°
2. 如图19,将三角形纸片ABC沿EF折叠可得图20(其中EF∥BC),已知图20的图形面积与原三角形的面积之比为3∶4,且阴影部分的面积为8,则原三角形面积为( ).
A.32 B.16 C.20 D.12
3. 把长为8cm的矩形按虚线对折,按图21中的虚线剪出一个直角梯形,打开得到一个等腰梯形,剪掉部分的面积为6cm2,则打开后梯形的周长是( )
A.(10+2)cm B.(10+)cm C.22cm D.18cm
4.图22-1是两个由同样大的小方格组成的图形,我们可以用不同的方法把这两个图形拼成一个轴对称图形,例如图22-2就是这样的轴对称图形,沿某条直线折叠后,直线两侧的图形能够完全重合.请问:符合要求的拼法一共有 种.
5.将任意三角形剪切可以拼成一个与此三角形面积相等的矩形.
方法如下(如图23—1):
请你类似上面图示的方法,解答下列的问题:
(1)对任意三角形(如图23—2),设计一种与上例不同的方案,将它分成若干块,再拼成一个与原三角形面积相等的矩形.
(2)对任意四边形(如图23—3),设计一种方案,将它分成若干块,再拼成一个与原四边形面积相等的矩形.
6.如图所示,左边方格纸中每个正方形的边长均为a,右边方格纸中每个正方形的边长均为b,将左边方格纸中的图形顺时针旋转90°,并按b:a的比例画在右边方格纸中.
随堂检测答案:
1.C ;2.D ;3.A ;4.3 ;
5.(1)
(2)
6.画图如下:
A
B
C
图4
D
E
A′
图12
D
C
B
A
A'
B'
O'
A
B
O
′
图14
图15
O'
A'
B'
A
O
′
′
B
y
x
8
7
6
5
4
3
2
1
0
8
7
6
5
4
3
2
1
B
C
A
图16
y
x
8
7
6
5
4
3
2
1
0
8
7
6
5
4
3
2
1
B
C
A
图17
E
D
B
C′
F
C
D′
A
图18
图19
图20
图21
②
图23—1
①
③
②
③
①
中点
中点
图23—2
图23—3
②
中点
中点
①
③
②
①
③
③
①
②
④
⑤
⑥
①
③
②
④
⑥
⑤
中点
中点
中点
中点
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
