函数的奇偶性(公开课)
图片预览





文档简介
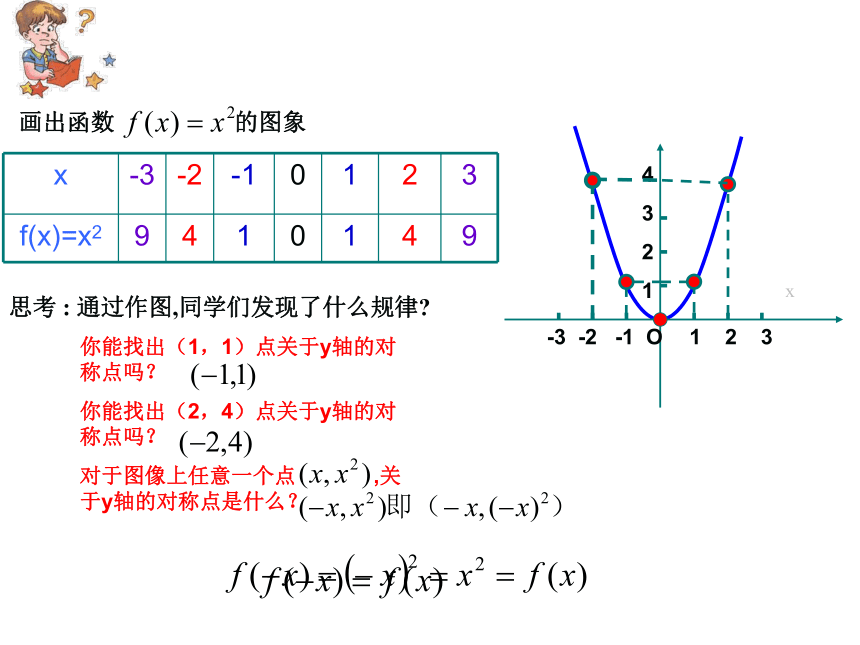
课件18张PPT。2.1.4函数的奇偶性画出函数 的图象你能找出(1,1)点关于y轴的对称点吗?
你能找出(2,4)点关于y轴的对称点吗?
对于图像上任意一个点 ,关于y轴的对称点是什么?
x思考 : 通过作图,同学们发现了什么规律?1.偶函数一般地,对于函数 的定义域内的任意一个 ,
都有 ,那么函数 就叫做偶函数. ☆对偶函数定义的说明: (1)函数是偶函数的的前提条件是:定义域关于原点对称。
(2)定义域内的任意x,都有f(-x)=f(x)成立. 概念辨析(判断下列说法是否正确)(1) 对于定义在R上的函数f(x),
若 ,则 f(x) 是偶函数;(2)函数 是偶函数;(×) (×)(×)(3)函数 是偶函数.例1. 判断下列函数是否是偶函数 (2)解:函数的定义域为R,
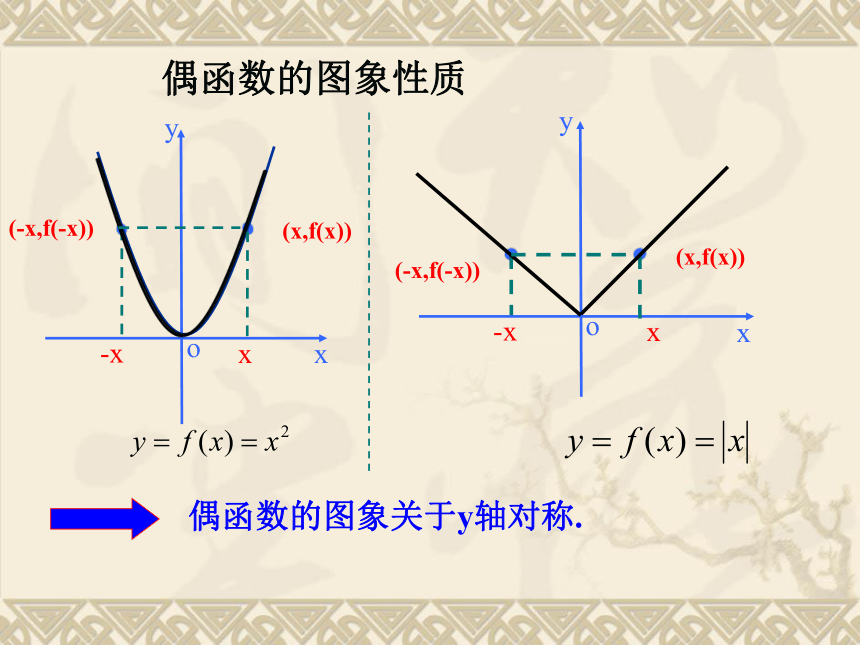
因为对定义域内的任意x,都有☆ 用定义判断函数是否是偶函数的步骤: ⑴先求出定义域,看定义域是否关于原点对称.⑵再判断f(-x)=f(x) 是否成立.偶函数的图象性质偶函数的图象关于y轴对称.ox(-x,f(-x))(x,f(x))-xox(-x,f(-x))(x,f(x))-xo解:画法略
解: g(-2)=(-2)3=-8 g (2)=8g(-1)=(-1)3=-1 g(1)=1 g(-x)=(-x)3=-x3思考 : 通过练习,同学们发现了什么规律?g(-2)= - g(2)
g(-1)= - g(1)
g(-x)= - g(x)2.奇函数 一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=-f(x),那么f(x)就叫做奇函数. 2.奇函数一般地,对于函数f(x)的定义域内的任意一个x,
都有f(-x)=-f(x),那么函数f(x)就叫做奇函数. ☆对奇函数定义的说明: (1)函数是奇函数前提条件是:定义域关于原点对称。
⑵定义域内的任意x,都有f(-x)=-f(x)成立.
☆ 用定义判断函数是否是奇函数的步骤: ⑴先求出定义域,看定义域是否关于原点对称.⑵再判断f(-x)= -f(x) 是否成立.证明:函数的定义域为 ,对于定义域内的任 意一个x,都有例3. 证明函数 是奇函数奇函数的图象oaaP/(-a ,f(-a))p(a ,f(a))-a(-a,-f(a))奇函数的图象关于原点对称.例 4 已知函数y=f(x)是奇函数,它在y轴右边的图象如图,画出y=f(x)在 y轴左边的图象。解:画法略想一想1. 函数有奇函数,偶函数,有没有函数既不是奇函数也不是偶函数的?
2.有没有这样的函数,它既是奇函数又是偶函数呢?1.两个定义: 对于f(x)定义域内的任意一个x ,
如果都有f(-x)=-f(x)
如果都有f(-x)= f(x)2.两个性质:
一个函数为奇函数 它的图象关于原点对称。一个函数为偶函数 它的图象关于y 轴对称。本课小结:作业:
P36练习 1.(2)(3)
2.谢谢!
你能找出(2,4)点关于y轴的对称点吗?
对于图像上任意一个点 ,关于y轴的对称点是什么?
x思考 : 通过作图,同学们发现了什么规律?1.偶函数一般地,对于函数 的定义域内的任意一个 ,
都有 ,那么函数 就叫做偶函数. ☆对偶函数定义的说明: (1)函数是偶函数的的前提条件是:定义域关于原点对称。
(2)定义域内的任意x,都有f(-x)=f(x)成立. 概念辨析(判断下列说法是否正确)(1) 对于定义在R上的函数f(x),
若 ,则 f(x) 是偶函数;(2)函数 是偶函数;(×) (×)(×)(3)函数 是偶函数.例1. 判断下列函数是否是偶函数 (2)解:函数的定义域为R,
因为对定义域内的任意x,都有☆ 用定义判断函数是否是偶函数的步骤: ⑴先求出定义域,看定义域是否关于原点对称.⑵再判断f(-x)=f(x) 是否成立.偶函数的图象性质偶函数的图象关于y轴对称.ox(-x,f(-x))(x,f(x))-xox(-x,f(-x))(x,f(x))-xo解:画法略
解: g(-2)=(-2)3=-8 g (2)=8g(-1)=(-1)3=-1 g(1)=1 g(-x)=(-x)3=-x3思考 : 通过练习,同学们发现了什么规律?g(-2)= - g(2)
g(-1)= - g(1)
g(-x)= - g(x)2.奇函数 一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=-f(x),那么f(x)就叫做奇函数. 2.奇函数一般地,对于函数f(x)的定义域内的任意一个x,
都有f(-x)=-f(x),那么函数f(x)就叫做奇函数. ☆对奇函数定义的说明: (1)函数是奇函数前提条件是:定义域关于原点对称。
⑵定义域内的任意x,都有f(-x)=-f(x)成立.
☆ 用定义判断函数是否是奇函数的步骤: ⑴先求出定义域,看定义域是否关于原点对称.⑵再判断f(-x)= -f(x) 是否成立.证明:函数的定义域为 ,对于定义域内的任 意一个x,都有例3. 证明函数 是奇函数奇函数的图象oaaP/(-a ,f(-a))p(a ,f(a))-a(-a,-f(a))奇函数的图象关于原点对称.例 4 已知函数y=f(x)是奇函数,它在y轴右边的图象如图,画出y=f(x)在 y轴左边的图象。解:画法略想一想1. 函数有奇函数,偶函数,有没有函数既不是奇函数也不是偶函数的?
2.有没有这样的函数,它既是奇函数又是偶函数呢?1.两个定义: 对于f(x)定义域内的任意一个x ,
如果都有f(-x)=-f(x)
如果都有f(-x)= f(x)2.两个性质:
一个函数为奇函数 它的图象关于原点对称。一个函数为偶函数 它的图象关于y 轴对称。本课小结:作业:
P36练习 1.(2)(3)
2.谢谢!
