指数函数及其性质

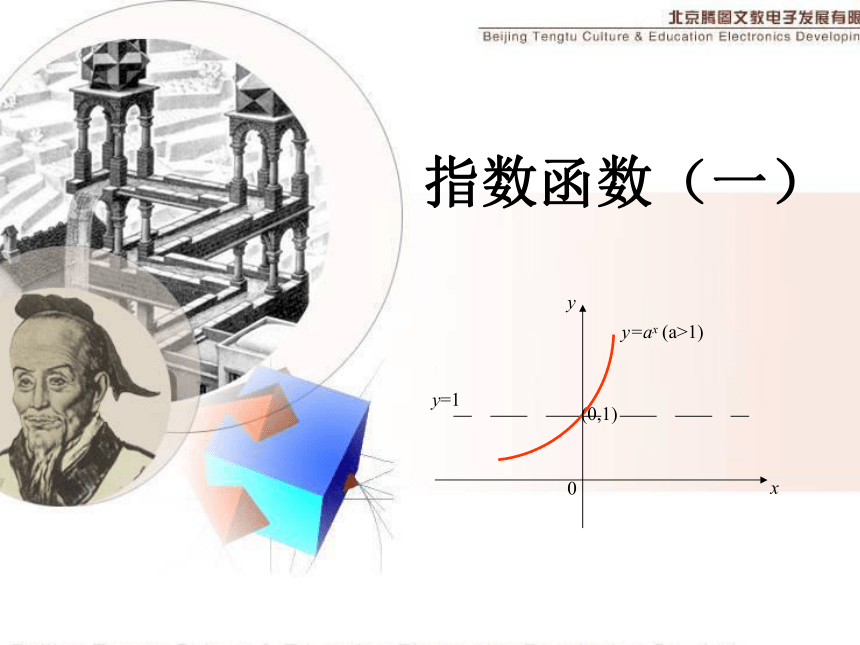
课件28张PPT。 2.6 指数函数及其性质授课教师： 陈轩 2008年11月21指数函数（一）
知识回顾1、我们之前学过哪几种类型的函数？ 常函数 y=a (a为实数） 正比例函数 y=kx (k≠0)反比例函数 y= (k ≠0)一次函数 y=ax+b (a ≠0)二次函数 y=a +bx+c (a ≠0）注意：在研究一个函数时一定要确定其定义域。R
R
R
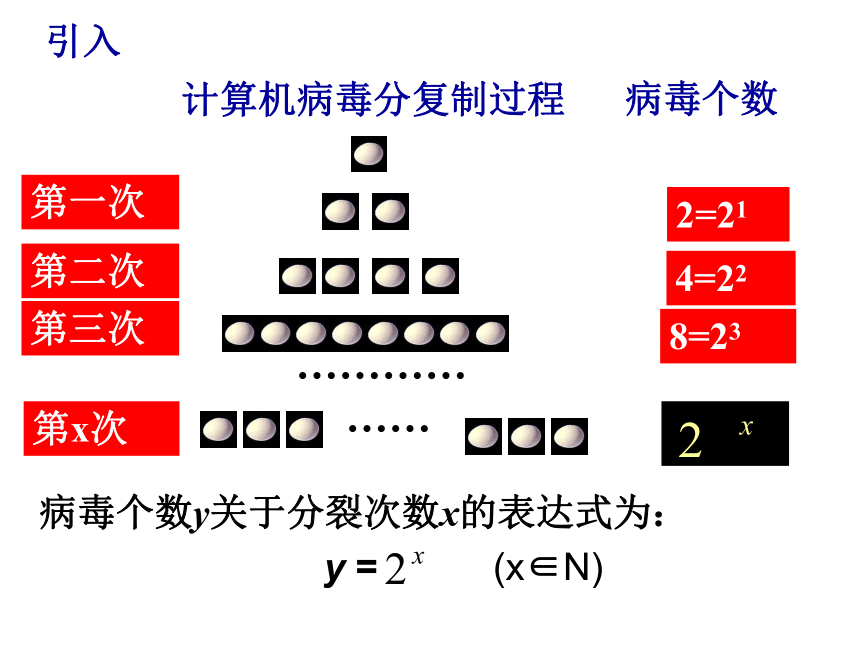
R问题一：计算机病毒的传播速度很快,可以由1个复制成2个,由2个复制成4个……若复制x次后得到的病毒个数y与次数x之间的函数关系式是？一、问题引入引入计算机病毒分复制过程病毒个数第一次第二次第三次2=218=234=22………… 第x次……病毒个数y关于分裂次数x的表达式为：y =
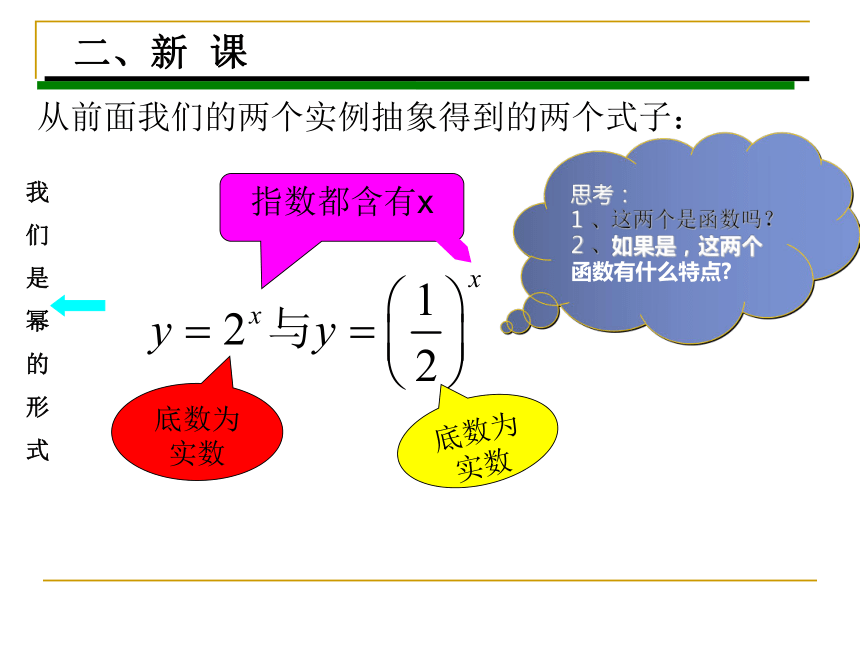
(x∈N)问题二、 一根1米长的绳子从中间剪一次剩下 米，再从中间剪一次剩下 米，若这条绳子剪x次剩下y米，则y与x的关系是：二、新 课 从前面我们的两个实例抽象得到的两个式子：思考：
1 、这两个是函数吗？
2 、如果是，这两个函数有什么特点?底数为实数底数为实数指数都含有x我
们
是
幂
的
形
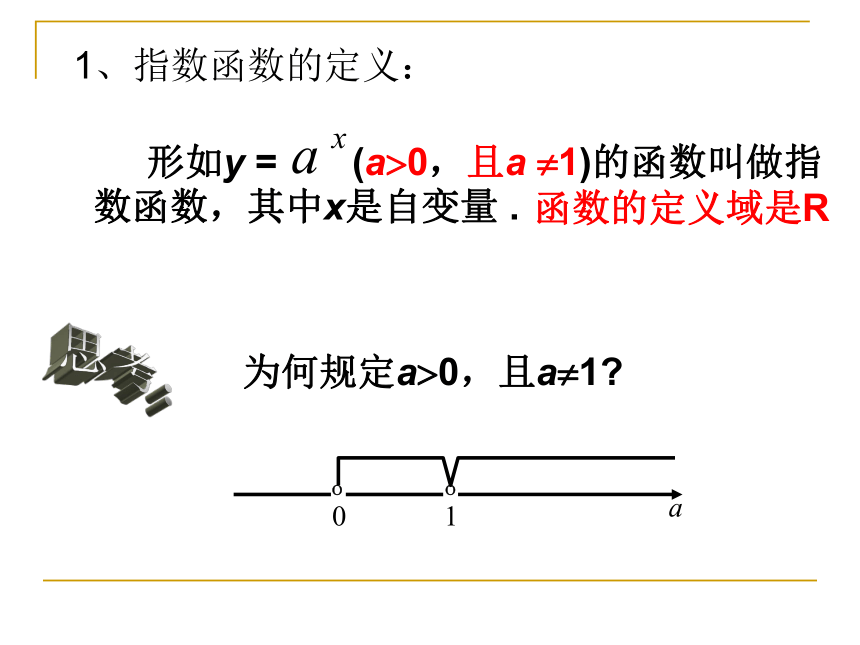
式1、指数函数的定义： 形如y = (a?0，且a ?1)的函数叫做指数函数，其中x是自变量 .思考：为何规定a?0，且a?1?
函数的定义域是R 当a?0时，ax 对有些数会没有意义，如(-2) ,0 等都没有意义；而当a=1时，函数值y恒等于1，没有研究的必要.记住：在y= 中a一定大于零！为何规定a?0，且a?1?
探究三、概念理解例1、指出下面哪个函数是指数函数：是否是否是(1)当k=1时，是；
(2)当k≠1时，否。思考：1 当a>1时， 的大致图像如下图： 学习函数的一般模式（方法）：解析式（定义）图像性质应用数形结合①定义域②值域③单调性⑤奇偶性④最值知识结构2.指数函数的图象和性质定义域为R，值域为(0,+?).过点（0，1），即当x=0时，y=1在R上是增函数y>1;
00时,
当x<0时, 当00时,
当x<0时,6.当x>0时,
当x<0时, 1.定义域为R，值域为(0,+?)4.非奇非偶函数4.非奇非偶函数02.过点（0，1）5.无最值5.无最值 y>1;
0 y>1;观察右边图象，回答问题： 问：从图形的对称性上看，右边函数图像有什么对称特征？
指数函数 与 的图像关于y轴对称；总结思考①当a>1时， 的图象随着a由小变大会有什么样的变化？②当01时， 的图象随着a由小变大会有越靠近y轴；②当00且a≠0）定义域为R。2、指数函数的图象与性质：
当0 当a>1时，它在R上是单调递增函数；并且指数函数一定通过（1，0）这个特殊点。作业： 理解指数函数的相关性质，并熟记！三、例题讲解例2、求下列函数的定义域：解、①②③二、新 课例3、比较下列各组数的大小：
解：①②、解：④、小结：比较指数大小的方法：①、构造函数法：要点是利用函数的单调性，数的特征是同底不同指（包括可以化为同底的），若底数是参变量要注意分类讨论。②、中间媒介法：用别的数如为媒介（如1等）。数的特征是不同底不同指。三、小结1、指数函数概念； 2、指数比较大小的方法； ①、构造函数法：要点是利用函数的单调性，数的特征是同底不同指（包括可以化为同底的），若底数是参变量要注意分类讨论。②、中间媒介法：用别的数如为媒介（如1等）。数的特征是不同底不同指。 形如y = ax(a?0，且a ?1)的函数叫做指数函数，其中x是自变量 .函数的定义域是R .3、指数函数的性质：（1）定义域： 值 域：（2）函数过特殊点：（3）函数的单调性：3.指数函数的图象和性质1.定义域为R，值域为(0,+?).2.图象都过点（0，1），即当x=0时，y=13.在R上是增函数3.在R上是减函数4.当x>0时,y>1;
当x<0时,00时, 0当x<0时, y>1.四、练习、作业1、练习P81 1、2
2、作业p82 1 、2