折叠与勾股定理

---八上专题—折叠问题与勾股定理---
[思路]
在直角三角形中勾股定理的作用:
1. 已知两边的长度，可求未知边的长度
2. 已知一边的长度以及另外两边的关系，可求未知边的长度（设未知数，列方程解决）
------------------------------------------------类型一--------------------------------------------------------
题1、如图，已知BC⊥CD，将线段BC在A处折断，使得刚好B、D两点重合。若BC=18，CD=12。求AC
[分析]：由BC=18，可得：AC+AB=18
又由折叠可得：AC+AD=18 （即已知两边的关系，故马上设未知数）
【解】设AC=x，则AB=，又AB折叠至AD，故AD=
于是，在Rt△ACD中，由勾股定理可得：
，解得
∴ AC=5
题2、在Rt△ABC，AB=3，BC=4，现将图形沿着AD对折，刚好使得B点落在AC边上的E处。
求△CDE的周长
【解】在Rt△ABC，由勾股定理可得：AC=
又由折叠可知：AE=AB=3，∴ CE=5-3=2
DE=BD
方法一： ∴ △CDE的周长=EC+CD+DE=EC+CD+BD=EC+BC=2+4=6
方法二： 设DE=，则BD，CD
故在折叠得到的Rt△CDE中，由勾股定理可得：，
解得，即BD=DE=，CD=
故△CDE的周长=EC+CD+DE=
变形练习：在Rt△ABC，AB=3，AC=5，现将图形沿着CD对折，刚好使得B点落在AC边上的E处。
求△ADE的周长
------------------------------------------------类型二--------------------------------------------------------
题3． 在长方形ABCD中，AB=8，BC=10，将图形沿着AE对折，使得D点落在BC边上的F处。试求EC的长。
[关键点]找到由折叠产生的所有等量关系，其中也需要用到方程思想（设未知数，并表示出其他线段长度）
【解】： 由题意可得：AD=BC=10，
又由折叠可知：AF=AD=10 DE=EF
∴ 在Rt△ABF中，根据勾股定理可得：
∴ BF=6， ∴ FC=10-6=4
设DE=，则，
故，在Rt△CEF中，根据勾股定理可得：
，解得：
即：DE=5
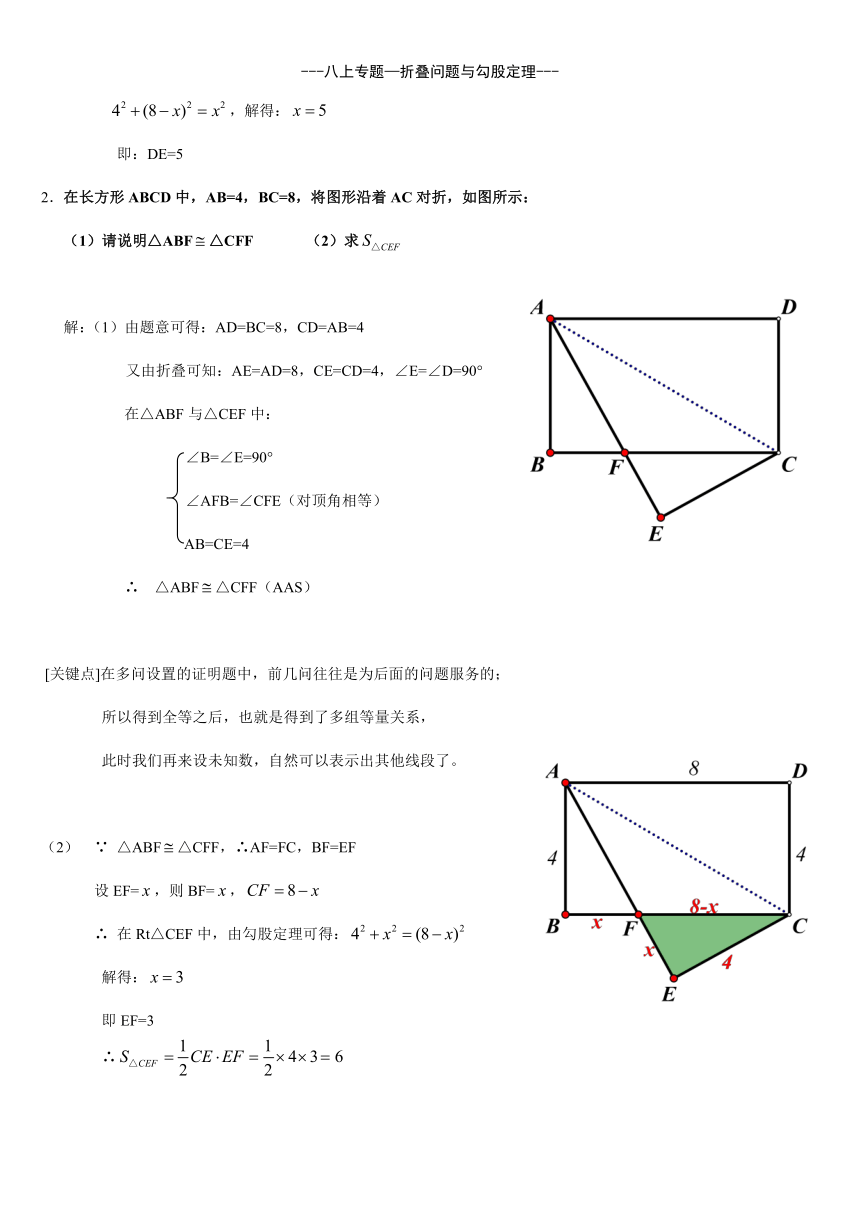
2．在长方形ABCD中，AB=4，BC=8，将图形沿着AC对折，如图所示：
（1）请说明△ABF△CFF （2）求
解：（1）由题意可得：AD=BC=8，CD=AB=4
又由折叠可知：AE=AD=8，CE=CD=4，∠E=∠D=90°
在△ABF与△CEF中：
∠B=∠E=90°
∠AFB=∠CFE（对顶角相等）
AB=CE=4
∴ △ABF△CFF（AAS）
[关键点]在多问设置的证明题中，前几问往往是为后面的问题服务的；
所以得到全等之后，也就是得到了多组等量关系，
此时我们再来设未知数，自然可以表示出其他线段了。
（2） ∵ △ABF△CFF，∴AF=FC，BF=EF
设EF=，则BF=，
∴ 在Rt△CEF中，由勾股定理可得：
解得：
即EF=3
∴
[补充]此题中对于△ABF，同样可以通过设未知数，利用勾股定理求解。
3．在长方形ABCD中，AB=3，BC=5，将图形沿着EF对折，使得B点与D点重合。
（1）说明DE=DF
（2）求
（3）求EF的长度
分析：（1）要说明DE=DF，有两种思路：
1 可说明全等；
② 可说明△DEF是等腰三角形，DE、DF是两腰
所以这个题目既要有能力说明全等也要有能力说明等腰
解：（1）方法一：由题意可得：CD=AB=3，∠ADC=90°
由折叠可得：DG=CD=3，∠G=∠C=90°，∠GDF=∠B=90°
∴ ∠1+∠2=90°，∠3+∠2=90° ∴ ∠1=∠3
故在△DEG与△DCF中：
∠G=∠C（已证）
DG=CD（已证） ∴ △DEG≌△DCF（ASA）
∠1=∠3（已证） ∴ DE=DF
方法二：∵ 长方形ABCD ∴ AD∥BC
∴ ∠4=∠6（两直线平行，内错角相等）
又由折叠可知∠4=∠5
∴ ∠5=∠6（等量代换）
∴ DE=DF（等角对等边）
[ 建议]
到现在为止，我们对待一个问题，要有能力去实现一题多解，对于较为简单的题目从多个角度用多种方法去思考，对于能力的培养非常重要，同学们在平时思考问题时要注意对这个能力的培养。
3．在长方形ABCD中，AB=3，BC=5，将图形沿着EF对折，使得B点与D点重合。
（2）求
解：由折叠可知：EG=AE
设，则，∴
故在Rt△DEG中，根据勾股定理可得：
解得：
故EG DE=
∴
变形练习：求△DEF的面积
思路：1.可以用梯形面积减去三角形的面积（因为前面已经说明图形中的两个直角三角形全等）
2. 若要直接求则需要做辅助线（做高）
若把DF当做底边，
则“过E点作EH⊥DF”，
∴ 四边形EHDG是长方形，
∴ EH=DG=3
若把DE当做底边，
则“过F点作FI⊥DE”，
∴ 四边形CDIF是长方形，
∴ IF=CD=3
3．在长方形ABCD中，AB=3，BC=5，将图形沿着EF对折，使得B点与D点重合。
（3）求EF的长度
分析：学完勾股定理之后，我们多了一种求线段长度的方法
解：易得ID=FC=，∴EI=
在Rt△EFI中，EF=
变形练习：如图，把矩形纸片沿折叠，使点落在边上的点处，点落在点处；
（1）求证：；
（2）设，试猜想之间的一种关系，并给予证明．
E
F
D
C
B
A