《垂径定理》复习学案

九年级上《垂径定理》复习学案
学习目标：
1. 通过复习，使学生进一步掌握圆的性质（垂径定理）。
2. 会熟练解决有关弦、弧、弦心距及半径之间关系的证明和计算。
3. 培养学生的探究能力和应用能力。
学习重点、难点：
垂径定理及逆定理的应用。
学习过程：
一、知识梳理 谁过关
垂径定理及其推论是《圆》一章的重要考点。定理告诉我们，对于一个圆和一条直线来说，如果具备如下五个条件中的两个，那么也具有另外的三个：①垂直于弦②过圆心③平分弦④平分弦所对的优弧⑤平分线所对的劣弧，它反映了圆的重要性质，是证明线段相等、角相等、垂直关系的重要依据，同时也为圆的计算和作图提供了方法和依据。
二、基础知识 谁最棒 （10分钟）
1．圆是轴对称图形，它的对称轴有 （ ）
A．一条 B 两条 C．一条 D．无数条
2． 如图1，在⊙O中，直径CD交弦AB（不是直径）于点E.
(1)若CD⊥AB，则有 、 、 ；
(2)若 AE = EB，则有 、 、 ；
(3)若 ，则有 、 、 .
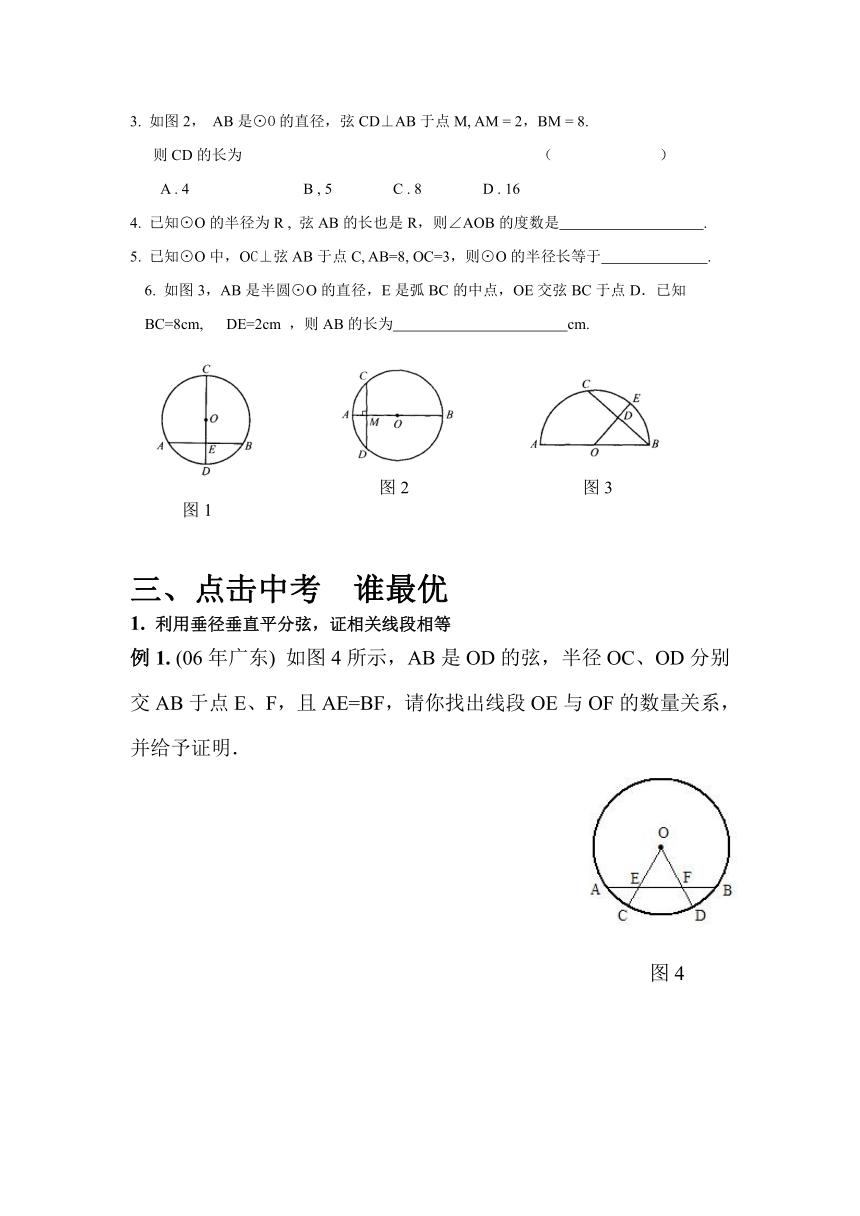
3. 如图2， AB是⊙O的直径，弦CD⊥AB于点M, AM = 2，BM = 8.
则CD的长为 （ ）
A . 4 B , 5 C . 8 D . 16
4. 已知⊙O的半径为R , 弦AB的长也是R，则∠AOB的度数是 .
5. 已知⊙O中，OC⊥弦AB于点C, AB=8, OC=3，则⊙O的半径长等于 .
6. 如图3，AB是半圆⊙O的直径，E是弧BC的中点，OE交弦BC于点D．已知BC=8cm, DE=2cm ，则AB的长为 cm.
图2 图3
图1
三、点击中考 谁最优
1. 利用垂径垂直平分弦，证相关线段相等
例1. (06年广东) 如图4所示，AB是OD的弦，半径OC、OD分别交AB于点E、F，且AE=BF，请你找出线段OE与OF的数量关系，并给予证明．
图4
2. 利用垂径垂直弦，构造成特殊四边形
例2（四川省）如图5，在⊙O中，AB、AC是互相垂直的两条弦， AB＝8cm，AC＝6cm，那么⊙O的半径OA的长 （ ）
A．4 cm B．5 cm C．6 cm D．8 cm
3. 利用垂径定理，构造直角三角形，利用勾股定理
例3（长春市）某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，图6是水平放置的破裂管道有水部分的截面．
（1）请你补全这个输水管道的圆形截面；
（2）若这个输水管道有水部分的水面宽AB＝16cm，水面最深地 方的高度为4cm，求这个圆形截面的半径．
四、挑战自我 谁能行 (15分钟)
1. 如图7，同心圆中，大圆的弦AB交小圆于C、D．已知AB= 4， CD=2，圆心O到AB的距离OE=1.则大、小两．圆的半径之比为 ( )
A. 3 : 2 B． C． D.．
2. 从圆上点所作的互相垂直的两弦．它们和圆心的距离分别为6cm和10cm，则此两弦的长分别为 .
3. ⊙O中弦AB⊥CD于点E, AB被CD分成5cm 和13cm两段，则圆心到CD的距离为 .
4. 一条弦把圆的一条直径分成2cm和6cm两部分，若弦与直径所成的角为300，则圆心到弦的距离为 .
5.如图8， ⊙O的直径为10，弦AB=8，P是弦AB上的一个动点，那么OP长的取值范围是 .
6. 已知⊙O的半径为10cm，弦MN//EF，且MN =12cm, EP=16cm，则弦MN和EF之间的距离为 .
图7 图8
7. 已知⊙O的半径为5cm，过⊙O内一点P的最短的弦长为8cm，则OP= .
在直径为650mm 的圆柱形油槽内装入一些油后，截面如图所示．若油面宽AB=600mm ，求油面的最大深度．
8. 如图，一条公路的转弯处是一段圆弧，点O是的圆心，E为的中点，OE交CD于点F. 已知CD=600m, EF=100m，求这段弯路的半径。
9.如图，直线AD交⊙O于点B、D, ⊙O的半径为10cm, AO=16cm，∠A=300，OC⊥AD于点C，求 BC, AB, AD的长，
五、我是总结小高手 谈谈你的收获
图6
图5