12.3.1(1)等腰三角形的性质学案
文档属性
| 名称 | 12.3.1(1)等腰三角形的性质学案 |
|
|
| 格式 | rar | ||
| 文件大小 | 62.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-18 00:00:00 | ||
图片预览


文档简介
第十二章 12.3.1《等腰三角形》---第1课时导学案
年级及科目:八年级数学 备课:董成伟 审核:八年级数学备课组 课型:展示课
【学习内容】§12.3.1《等腰三角形》,教材第49--51页
【学习目标】
(一)知识技能
1.掌握等腰三角形的有关概念和性质;
2.熟练运用等腰三角形的性质解决等腰三角形内角以及边的证明和计算问题。
(二)过程与方法
1.在探索等腰三角形的性质和判定的过程中体会知识间的关系,感受数学与生活的联系;
2.培养学生添加辅助线解决问题的能力。
(三)情感态度与价值观
1.通过学生之间的交流活动,培养学生主动与他人合作交流的意识;
2.培养学生分析解决问题的能力,使学生养成良好的学习习惯。
【学习重点】
探索和掌握等腰三角形的性质及其应用。
【学习难点】
等腰三角形的性质的证明。
【学习方法】
预习展示
【学习过程】
探究1:
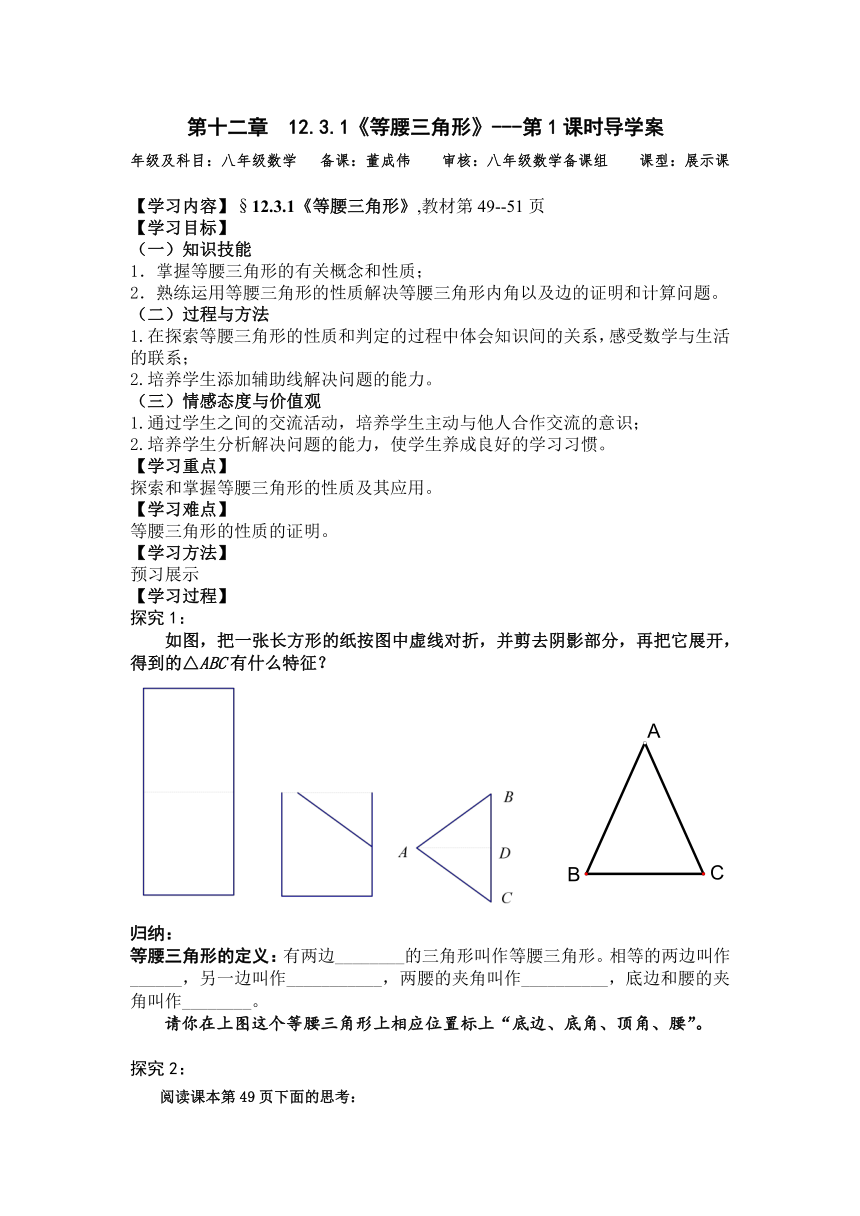
如图,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC有什么特征?
归纳:
等腰三角形的定义:有两边________的三角形叫作等腰三角形。相等的两边叫作______,另一边叫作___________,两腰的夹角叫作__________,底边和腰的夹角叫作________。
请你在上图这个等腰三角形上相应位置标上“底边、底角、顶角、腰”。
探究2:
阅读课本第49页下面的思考:
(1)把探究1中剪出的△ABC沿折痕AD对折,找出其中重合的线段,填入下表:
重合的线段 重合的角
(2)从上表中你能发现等腰三角形具有什么性质吗?
等腰三角形的性质:
性质1 (简写成“ ” );
性质2 。(简写成“ ” )
注意:性质2实际上包含了三个命题:(1) ;
(2) ;(3) 。
活动1:
你能用所学知识验证上述性质吗?
例:
求证:等腰三角形的两个底角相等。
已知: ΔABC中,AB=AC.
求证: ∠B= ∠C.
证明;作底边BC的中线AD.
在△BAD和△CAD中,
AB=AC
AD=AD
BD=CD( 辅助线作法 )
∴ △BAD ≌ △CAD ( ).
∴ ∠ B= ∠C ( ).
请思考:
作底边上的高可以吗?作顶角的平分线可以吗?
请思考:
怎样证明性质2呢?(提示:实际上是证明性质2包含的三个命题)
活动2:
等腰三角形性质定理的推理格式:
(1)∵AB=AC,∴____= ____. (等边对等角)
(2)∵AB=AC,AD是角平分线,∴____ ⊥____ ,_____ =_____.(三线合一)
∵AB=AC,AD是中线,∴____⊥____ ,∠_____ =∠_____.(三线合一)
∵AB=AC ,AD⊥BC,∴∠_____ = ∠_____,____= ____. (三线合一)
归纳:
“三线合一”的运用过程可理解为“知一推二”(即在等腰三角形中,知“一线”可推出“另两线”)
活动3:
典例分析
1.如图,在△ABC中,AB=AC,点D在AC上,且BD = BC = AD,求△ABC各角的度数。
2.如图,D、E在△ABC的边BC上,AB=AC,AD=AE,求证:BD=CE。
活动4:当堂训练
1、 等腰三角形的对称轴是( )
A、顶角的平分线 B、底边上的高
C、底边上的中线 D、底边上的高所在的直线
2、如图,把一张对边平行的纸条如图折叠,重合部分是 ( )
A、等边三角形 B、等腰三角形
C、直角三角形 D、无法确定
3、等腰三角形的一个外角是80°,则其底角是( )
A、100° B、100°或40° C、40° D、80
4、等腰三角形的两边长分别是4和9,则其周长是( )
A、22 B、17 C、22或17 D、27
5、如图,在四边形ABCD中,AB=AD,CB=CD,求证:∠ABC=∠ADC。
6、在△ ABC中,AB=AD=DC, ∠BAD=26°,求∠ B和∠ C的度数
活动5:目标检测
1、(2009年贵州黔东南)如图2,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )
A、30o B、40o C、45o D、36o
2、(2009年烟台)如图,等边的边长为3,为上一点,
且,为上一点,若,则
的长为( )
A、 B、 C、 D、
3、(2009年杭州)若一个等腰三角形的一个外角等于110 o ,则这个等腰三角形的度数分别为 。
4、等腰三角形一腰上的高与另一腰的夹角为30 o ,则顶角的度数为( )
A、 60 o B、 120 o C 、 60 o 或150 o D、60 o或120 o
5、(2009年呼和浩特)在等腰△ABC中,AB=AC,中线BD将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为( )
A、7 B、11 C、7或11 D、7或10
6、(2009年威海)如图,,若, 则的度数是( )
A、 B、 C、 D、
7、如图,在△ABC中,AB=AC,O为△ABC内的一点,且OB=OC。
求证:AO⊥BC。
8、(挑战题)如图,在△ABC中,AB=AC,AD=AE,若∠BAD=20 o,
求∠CDE的度数。
活动6:学习小结
1、 。
2、 。
A
B
60°
P
B
C
D
A
C
D
这是运用“三线合一”
的前提条件!
年级及科目:八年级数学 备课:董成伟 审核:八年级数学备课组 课型:展示课
【学习内容】§12.3.1《等腰三角形》,教材第49--51页
【学习目标】
(一)知识技能
1.掌握等腰三角形的有关概念和性质;
2.熟练运用等腰三角形的性质解决等腰三角形内角以及边的证明和计算问题。
(二)过程与方法
1.在探索等腰三角形的性质和判定的过程中体会知识间的关系,感受数学与生活的联系;
2.培养学生添加辅助线解决问题的能力。
(三)情感态度与价值观
1.通过学生之间的交流活动,培养学生主动与他人合作交流的意识;
2.培养学生分析解决问题的能力,使学生养成良好的学习习惯。
【学习重点】
探索和掌握等腰三角形的性质及其应用。
【学习难点】
等腰三角形的性质的证明。
【学习方法】
预习展示
【学习过程】
探究1:
如图,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC有什么特征?
归纳:
等腰三角形的定义:有两边________的三角形叫作等腰三角形。相等的两边叫作______,另一边叫作___________,两腰的夹角叫作__________,底边和腰的夹角叫作________。
请你在上图这个等腰三角形上相应位置标上“底边、底角、顶角、腰”。
探究2:
阅读课本第49页下面的思考:
(1)把探究1中剪出的△ABC沿折痕AD对折,找出其中重合的线段,填入下表:
重合的线段 重合的角
(2)从上表中你能发现等腰三角形具有什么性质吗?
等腰三角形的性质:
性质1 (简写成“ ” );
性质2 。(简写成“ ” )
注意:性质2实际上包含了三个命题:(1) ;
(2) ;(3) 。
活动1:
你能用所学知识验证上述性质吗?
例:
求证:等腰三角形的两个底角相等。
已知: ΔABC中,AB=AC.
求证: ∠B= ∠C.
证明;作底边BC的中线AD.
在△BAD和△CAD中,
AB=AC
AD=AD
BD=CD( 辅助线作法 )
∴ △BAD ≌ △CAD ( ).
∴ ∠ B= ∠C ( ).
请思考:
作底边上的高可以吗?作顶角的平分线可以吗?
请思考:
怎样证明性质2呢?(提示:实际上是证明性质2包含的三个命题)
活动2:
等腰三角形性质定理的推理格式:
(1)∵AB=AC,∴____= ____. (等边对等角)
(2)∵AB=AC,AD是角平分线,∴____ ⊥____ ,_____ =_____.(三线合一)
∵AB=AC,AD是中线,∴____⊥____ ,∠_____ =∠_____.(三线合一)
∵AB=AC ,AD⊥BC,∴∠_____ = ∠_____,____= ____. (三线合一)
归纳:
“三线合一”的运用过程可理解为“知一推二”(即在等腰三角形中,知“一线”可推出“另两线”)
活动3:
典例分析
1.如图,在△ABC中,AB=AC,点D在AC上,且BD = BC = AD,求△ABC各角的度数。
2.如图,D、E在△ABC的边BC上,AB=AC,AD=AE,求证:BD=CE。
活动4:当堂训练
1、 等腰三角形的对称轴是( )
A、顶角的平分线 B、底边上的高
C、底边上的中线 D、底边上的高所在的直线
2、如图,把一张对边平行的纸条如图折叠,重合部分是 ( )
A、等边三角形 B、等腰三角形
C、直角三角形 D、无法确定
3、等腰三角形的一个外角是80°,则其底角是( )
A、100° B、100°或40° C、40° D、80
4、等腰三角形的两边长分别是4和9,则其周长是( )
A、22 B、17 C、22或17 D、27
5、如图,在四边形ABCD中,AB=AD,CB=CD,求证:∠ABC=∠ADC。
6、在△ ABC中,AB=AD=DC, ∠BAD=26°,求∠ B和∠ C的度数
活动5:目标检测
1、(2009年贵州黔东南)如图2,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )
A、30o B、40o C、45o D、36o
2、(2009年烟台)如图,等边的边长为3,为上一点,
且,为上一点,若,则
的长为( )
A、 B、 C、 D、
3、(2009年杭州)若一个等腰三角形的一个外角等于110 o ,则这个等腰三角形的度数分别为 。
4、等腰三角形一腰上的高与另一腰的夹角为30 o ,则顶角的度数为( )
A、 60 o B、 120 o C 、 60 o 或150 o D、60 o或120 o
5、(2009年呼和浩特)在等腰△ABC中,AB=AC,中线BD将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为( )
A、7 B、11 C、7或11 D、7或10
6、(2009年威海)如图,,若, 则的度数是( )
A、 B、 C、 D、
7、如图,在△ABC中,AB=AC,O为△ABC内的一点,且OB=OC。
求证:AO⊥BC。
8、(挑战题)如图,在△ABC中,AB=AC,AD=AE,若∠BAD=20 o,
求∠CDE的度数。
活动6:学习小结
1、 。
2、 。
A
B
60°
P
B
C
D
A
C
D
这是运用“三线合一”
的前提条件!
