苏教版必修4第二章《平面向量》前三节
图片预览











文档简介
课件35张PPT。镇江市网络同步助学平台苏教版必修4第二章《平面向量》
§2.1:向量的概念及表示;
§2.2:向量的线性运算;
§2.3:向量的坐标表示;1苏教版必修4第二章《平面向量》前三节 一.向量的有关概念及表示;
二.向量的运算;
三.平面向量基本定理;
四.归纳总结.目 录1一、向量的有关概念1.向量的定义:既有大小又有方向的量.注意:如果向量的起点在原点,那么向量
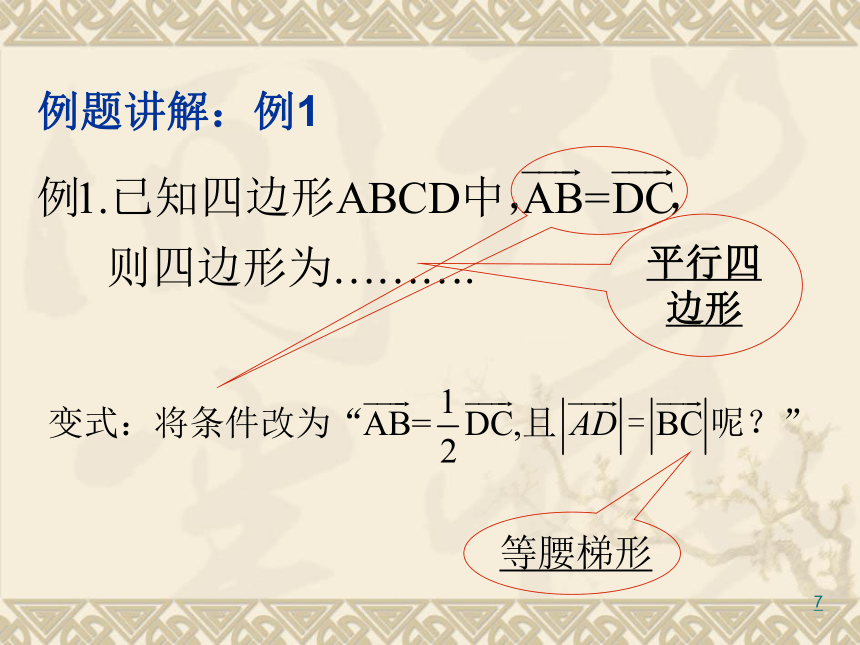
的坐标与向量的终点坐标相同。 15.相等向量:大小相等,方向相同的向量.1不能=01例题讲解:例1平行四边形等腰梯形1例2:对于下列各种情况,各向量的终点的集合分别是什么图形?
(1)把平行于直线m的所有单位向量的起点平移到m上的点p;例题讲解:例2解:直线上与点p距离为1的两个点
PAB1(2)把所有单位向量的起点平行移动到同一点p;(3)把平行于直线m的一切向量的起点
平移到m上的点p. 解:集合表示以p为圆心,
1个单位长为半径的圆; 解:直线m. PP解:集合表示以p为圆心,
1个单位长为半径的圆; 1二、向量的运算 1.几何运算:
①向量加法:利用“平行四边形法则”进行,
但“平行四边形法则”只适用于不共线的向量,
除此之外,向量加法还可利用“三角形法则”:
设, 那么向量 叫做 与 的和,
即 ;注意运用:
一个封闭图形首尾连接而成的向量和为零向量.1②向量的减法:用“三角形法则”:
设 ,
由减向量的终点指向被减向量的终点
注意:此处减向量与被减向量的起点相同。 1
实数 与向量 的积是一个向量,记作 ,
它的长度和方向规定如下:
当 时, 的方向与 的方向相同,
当 时, 的方向与 的方向相反,
当 时, .
注意: .2.实数与向量的积:1 设 ,则:
①向量的加减法运算: , 3.坐标运算: 设 ,则:
①向量的加减法运算: , 设 ,则:
①向量的加减法运算: , 设 ,则:
①向量的加减法运算: , 当 时, 表示 方向上的单位向量 .14.向量的运算律1提醒: 向量运算和实数运算有类似的地方也有区别:对于一个向量等式,可以移项,两边平方、两边同乘以一个实数,两边同时取模,两边同乘以一个向量,但不能两边同除以一个向量,即两边不能约去一个向量,切记两向量不能相除(相约);15.共线定理向量平行(共线)的充要条件: 规定: 与任何向量平行.1例题讲解:例3错解:(8,-5)分析:向量为自由向量,平移不改变向量的大小和方向.1例题讲解:例4如图,四边形 是以向量
为边的平行四边形,又
试用 表示向量1分析:把所求向量放到三角形或平行四边形中, 运用法则进行求解.解:1例题讲解:例5已知 =(1,0), =(2,1),当实数 为何值时,
向量 平行?并确定此
时它们是同向还是反向. 分析:利用向量平行(共线)的充要条件:1解:从而它们方向相反.1点评:
例5主要考查了向量的坐标运算和向量共线的充要条件.1例题讲解:例6已知点 .
(1)要使点 在 轴上、 轴上、第二象限内,
则 分别应取什么值?
(2)四边形 是否有可能是平行四边形?
如可能,求出 相应的值,
如不可能说明理由.1分析:
(1)当向量的起点为坐标原点时,
向量的坐标即为向量的终点坐标;
11(2)四边形 是否有可能是平行四边形?
如可能,求出 相应的值,如不可能说明
理由.分析:要使四边形为平行四边形,只需
有一对边向量相等.1若四边形 是平行四边形得:所以t无解.故四边形OABP不可能是平行四边形1点评:
例6主要考查了向量的坐标表示和
坐标运算,以及向量相等的概念.1三、平面向量的基本定理 如果 和 是同一平面内的两个不共线向量,
那么对该平面内的任一向量 ,
有且只有一对实数 、 ,
使1例题讲解:例7设 是平面的一组基底,如果
求证: 三点共线.分析:欲证 三点共线,只需证明
共起点的两个向量 共线,
即证11例题讲解:例8在平面直角坐标系中, 为坐标原点,已知
两点 ,若点 满足
其中 ,且 ,
求点 的轨迹方程. 分析: 的坐标即为 的坐标;可令 的坐
标,则 的坐标满足的等式即为点 的轨迹方程.1解:设 ,点 满足 ,
所以 ,
解得 又 ,
所以点 的轨迹方程为 .想一想:
怎么解得?1四、归纳总结1.要熟记向量的有关概念和公式;
2.填空题中常以三角形和平行四边形为载体
考查向量的概念和运算;
3.判断两向量是否共线,已知两向量共线求
参数问题;
4.平面向量基本定理及坐标表示的综合问题;
5.点共线转化为向量共线问题;
1再 见 祝同学们学习愉快! 本次讲座到此结束1
§2.1:向量的概念及表示;
§2.2:向量的线性运算;
§2.3:向量的坐标表示;1苏教版必修4第二章《平面向量》前三节 一.向量的有关概念及表示;
二.向量的运算;
三.平面向量基本定理;
四.归纳总结.目 录1一、向量的有关概念1.向量的定义:既有大小又有方向的量.注意:如果向量的起点在原点,那么向量
的坐标与向量的终点坐标相同。 15.相等向量:大小相等,方向相同的向量.1不能=01例题讲解:例1平行四边形等腰梯形1例2:对于下列各种情况,各向量的终点的集合分别是什么图形?
(1)把平行于直线m的所有单位向量的起点平移到m上的点p;例题讲解:例2解:直线上与点p距离为1的两个点
PAB1(2)把所有单位向量的起点平行移动到同一点p;(3)把平行于直线m的一切向量的起点
平移到m上的点p. 解:集合表示以p为圆心,
1个单位长为半径的圆; 解:直线m. PP解:集合表示以p为圆心,
1个单位长为半径的圆; 1二、向量的运算 1.几何运算:
①向量加法:利用“平行四边形法则”进行,
但“平行四边形法则”只适用于不共线的向量,
除此之外,向量加法还可利用“三角形法则”:
设, 那么向量 叫做 与 的和,
即 ;注意运用:
一个封闭图形首尾连接而成的向量和为零向量.1②向量的减法:用“三角形法则”:
设 ,
由减向量的终点指向被减向量的终点
注意:此处减向量与被减向量的起点相同。 1
实数 与向量 的积是一个向量,记作 ,
它的长度和方向规定如下:
当 时, 的方向与 的方向相同,
当 时, 的方向与 的方向相反,
当 时, .
注意: .2.实数与向量的积:1 设 ,则:
①向量的加减法运算: , 3.坐标运算: 设 ,则:
①向量的加减法运算: , 设 ,则:
①向量的加减法运算: , 设 ,则:
①向量的加减法运算: , 当 时, 表示 方向上的单位向量 .14.向量的运算律1提醒: 向量运算和实数运算有类似的地方也有区别:对于一个向量等式,可以移项,两边平方、两边同乘以一个实数,两边同时取模,两边同乘以一个向量,但不能两边同除以一个向量,即两边不能约去一个向量,切记两向量不能相除(相约);15.共线定理向量平行(共线)的充要条件: 规定: 与任何向量平行.1例题讲解:例3错解:(8,-5)分析:向量为自由向量,平移不改变向量的大小和方向.1例题讲解:例4如图,四边形 是以向量
为边的平行四边形,又
试用 表示向量1分析:把所求向量放到三角形或平行四边形中, 运用法则进行求解.解:1例题讲解:例5已知 =(1,0), =(2,1),当实数 为何值时,
向量 平行?并确定此
时它们是同向还是反向. 分析:利用向量平行(共线)的充要条件:1解:从而它们方向相反.1点评:
例5主要考查了向量的坐标运算和向量共线的充要条件.1例题讲解:例6已知点 .
(1)要使点 在 轴上、 轴上、第二象限内,
则 分别应取什么值?
(2)四边形 是否有可能是平行四边形?
如可能,求出 相应的值,
如不可能说明理由.1分析:
(1)当向量的起点为坐标原点时,
向量的坐标即为向量的终点坐标;
11(2)四边形 是否有可能是平行四边形?
如可能,求出 相应的值,如不可能说明
理由.分析:要使四边形为平行四边形,只需
有一对边向量相等.1若四边形 是平行四边形得:所以t无解.故四边形OABP不可能是平行四边形1点评:
例6主要考查了向量的坐标表示和
坐标运算,以及向量相等的概念.1三、平面向量的基本定理 如果 和 是同一平面内的两个不共线向量,
那么对该平面内的任一向量 ,
有且只有一对实数 、 ,
使1例题讲解:例7设 是平面的一组基底,如果
求证: 三点共线.分析:欲证 三点共线,只需证明
共起点的两个向量 共线,
即证11例题讲解:例8在平面直角坐标系中, 为坐标原点,已知
两点 ,若点 满足
其中 ,且 ,
求点 的轨迹方程. 分析: 的坐标即为 的坐标;可令 的坐
标,则 的坐标满足的等式即为点 的轨迹方程.1解:设 ,点 满足 ,
所以 ,
解得 又 ,
所以点 的轨迹方程为 .想一想:
怎么解得?1四、归纳总结1.要熟记向量的有关概念和公式;
2.填空题中常以三角形和平行四边形为载体
考查向量的概念和运算;
3.判断两向量是否共线,已知两向量共线求
参数问题;
4.平面向量基本定理及坐标表示的综合问题;
5.点共线转化为向量共线问题;
1再 见 祝同学们学习愉快! 本次讲座到此结束1
