高中数学课件 新人教版必修3:7算法案例(1)
文档属性
| 名称 | 高中数学课件 新人教版必修3:7算法案例(1) |  | |
| 格式 | rar | ||
| 文件大小 | 138.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-18 08:13:00 | ||
图片预览





文档简介
课件17张PPT。1.3算法案例(第一课时)表示算法的三种方式:算法步骤(自然语言)程序框图(图形语言)计算机程序(程序语言)复习引入3 159 45[问题1]:在小学,我们已经学过求最大公约数的知识,你能求出18与90的最大公约数吗?18 9023∴18和90的最大公约数是2×3×3=18.先用两个数公有的质因数连续去除,一直除到所得的商是互质数为止,然后把所有的除数连乘起来.[问题2]:求8251与6105的最大公约数?新课讲解1 53求两个正数8251和6105的最大公约数。解:8251=6105×1+2146;6105=2146×2+1813;
2146=1813×1+333;
1813=333×5+148;
333=148×2+37;
148=37×4+0.则37为8251与6105的最大公约数。 以上我们求最大公约数的方法就是辗转相除法。也叫欧几里德算法,它是由欧几里德在公元前300年左右首先提出的。 研探新知一、辗转相除法(欧几里得算法)1、定义:
所谓辗转相除法,就是对于给定的两个数,用较大的数除以较小的数。若余数不为零,则将除数变被除数,余数变除数,继续上面的除法,直到大数被小数除尽,则这时最后的除数就是原来两个数的最大公约数。辗转相除法是一个反复执行直到余数等于0停止的算法 [问题3]你能把辗转相除法写成算法步骤吗?研探新知第四步,若r=0,则m,n的最大公约数等于m;
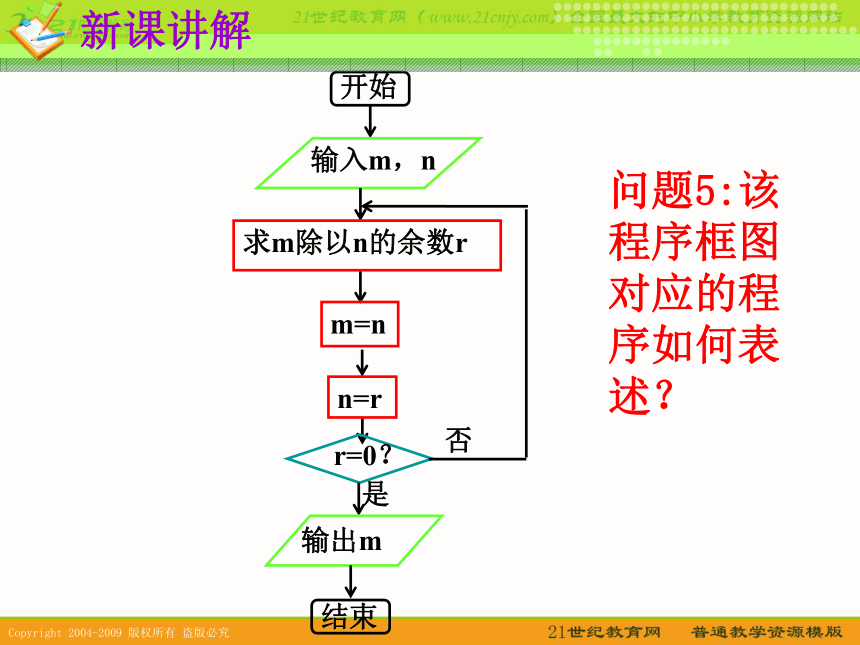
否则,返回第二步辗转相除法求最大公约数算法步骤:第一步,给定两个正数m,n第二步,计算m除以n所得到余数r第三步,m=n,n=r研探新知[问题4]:该算法的程序框图如何表示?求m除以n的余数r新课讲解问题5:该程序框图对应的程序如何表述?INPUT m,nDOr=m MOD nm=nn=rLOOP UNTIL r=0PRINT mEND求m除以n的余数rm=nn=r新课讲解问题6:如果用当型循环结构构造算法,求两个正整数m,n的最大公约数的程序框图和程序分别如何表示?研探新知例2 用更相减损术求98与63的最大公约数. 解:由于63不是偶数,把98和63以大数减小数,并辗转相减, 即:98-63=35;
63-35=28;
35-28=7;
28-7=21;
21-7=14;
14-7=7.所以,98与63的最大公约数是7。练习2:用更相减损术求两个正数84与72的最大公约数。 (12)研探新知辗转相除法与更相减损术的比较: (1)都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主;计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显。
(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损术则以减数与差相等而得到.研探新知思考2:上述求两个正整数的最大公约数的方法称为更相减损术.一般地,用更相减损术求两个正整数m,n的最大公约数,可以用什么逻辑结构来构造算法?其算法步骤如何设计?第一步,给定两个正整数m,n(m>n). 第二步,计算m-n所得的差k. 第三步,比较n与k的大小,其中大者用m表 示,小者用n表示. 第四步,若m=n,则m,n的最大公约数等于 m;否则,返回第二步. 研探新知思考3:该算法的程序框图如何表示?研探新知思考4:该程序框图对应的程序如何表述?INPUT m,nWHILE m<>nk=m-nIF n>k THENm=nn=kELSEm=kEND IFWENDPRINT mEND研探新知1、分别用辗转相除法和更相减损术求168与93的最大公约数. 辗转相除法:168=93×1+75,
93=75×1+18,
75=18×4+3,
18=3×6.练习更相减损术:168-93=75, 93-75=18,
75-18=57, 57-18=39,
39-18=21, 21-18=3,
18-3=15, 15-3=12,
12-3=9, 9-3=6,
6-3=3. 1.辗转相除法,就是对于给定的两个正整数,用较大的数除以较小的数,若余数不为零,则将余数和较小的数构成新的一对数,继续上面的除法,直到大数被小数除尽为止,这时的较小的数即为原来两个数的最大公约数. 2. 更相减损术,就是对于给定的两个正整数,用较大的数减去较小的数,然后将差和较小的数构成新的一对数,继续上面的减法,直到差和较小的数相等,此时相等的两数即为原来两个数的最大公约数.小结与作业3、辗转相除法与更相减损术的区别
(1)都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主,计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显。
(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损术则以减数与差相等而得到小结与作业课本P48页练习T1;
2146=1813×1+333;
1813=333×5+148;
333=148×2+37;
148=37×4+0.则37为8251与6105的最大公约数。 以上我们求最大公约数的方法就是辗转相除法。也叫欧几里德算法,它是由欧几里德在公元前300年左右首先提出的。 研探新知一、辗转相除法(欧几里得算法)1、定义:
所谓辗转相除法,就是对于给定的两个数,用较大的数除以较小的数。若余数不为零,则将除数变被除数,余数变除数,继续上面的除法,直到大数被小数除尽,则这时最后的除数就是原来两个数的最大公约数。辗转相除法是一个反复执行直到余数等于0停止的算法 [问题3]你能把辗转相除法写成算法步骤吗?研探新知第四步,若r=0,则m,n的最大公约数等于m;
否则,返回第二步辗转相除法求最大公约数算法步骤:第一步,给定两个正数m,n第二步,计算m除以n所得到余数r第三步,m=n,n=r研探新知[问题4]:该算法的程序框图如何表示?求m除以n的余数r新课讲解问题5:该程序框图对应的程序如何表述?INPUT m,nDOr=m MOD nm=nn=rLOOP UNTIL r=0PRINT mEND求m除以n的余数rm=nn=r新课讲解问题6:如果用当型循环结构构造算法,求两个正整数m,n的最大公约数的程序框图和程序分别如何表示?研探新知例2 用更相减损术求98与63的最大公约数. 解:由于63不是偶数,把98和63以大数减小数,并辗转相减, 即:98-63=35;
63-35=28;
35-28=7;
28-7=21;
21-7=14;
14-7=7.所以,98与63的最大公约数是7。练习2:用更相减损术求两个正数84与72的最大公约数。 (12)研探新知辗转相除法与更相减损术的比较: (1)都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主;计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显。
(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损术则以减数与差相等而得到.研探新知思考2:上述求两个正整数的最大公约数的方法称为更相减损术.一般地,用更相减损术求两个正整数m,n的最大公约数,可以用什么逻辑结构来构造算法?其算法步骤如何设计?第一步,给定两个正整数m,n(m>n). 第二步,计算m-n所得的差k. 第三步,比较n与k的大小,其中大者用m表 示,小者用n表示. 第四步,若m=n,则m,n的最大公约数等于 m;否则,返回第二步. 研探新知思考3:该算法的程序框图如何表示?研探新知思考4:该程序框图对应的程序如何表述?INPUT m,nWHILE m<>nk=m-nIF n>k THENm=nn=kELSEm=kEND IFWENDPRINT mEND研探新知1、分别用辗转相除法和更相减损术求168与93的最大公约数. 辗转相除法:168=93×1+75,
93=75×1+18,
75=18×4+3,
18=3×6.练习更相减损术:168-93=75, 93-75=18,
75-18=57, 57-18=39,
39-18=21, 21-18=3,
18-3=15, 15-3=12,
12-3=9, 9-3=6,
6-3=3. 1.辗转相除法,就是对于给定的两个正整数,用较大的数除以较小的数,若余数不为零,则将余数和较小的数构成新的一对数,继续上面的除法,直到大数被小数除尽为止,这时的较小的数即为原来两个数的最大公约数. 2. 更相减损术,就是对于给定的两个正整数,用较大的数减去较小的数,然后将差和较小的数构成新的一对数,继续上面的减法,直到差和较小的数相等,此时相等的两数即为原来两个数的最大公约数.小结与作业3、辗转相除法与更相减损术的区别
(1)都是求最大公约数的方法,计算上辗转相除法以除法为主,更相减损术以减法为主,计算次数上辗转相除法计算次数相对较少,特别当两个数字大小区别较大时计算次数的区别较明显。
(2)从结果体现形式来看,辗转相除法体现结果是以相除余数为0则得到,而更相减损术则以减数与差相等而得到小结与作业课本P48页练习T1;
