24.1.2 垂直于弦的直径(1)
文档属性
| 名称 | 24.1.2 垂直于弦的直径(1) |

|
|
| 格式 | rar | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-17 00:00:00 | ||
图片预览


文档简介
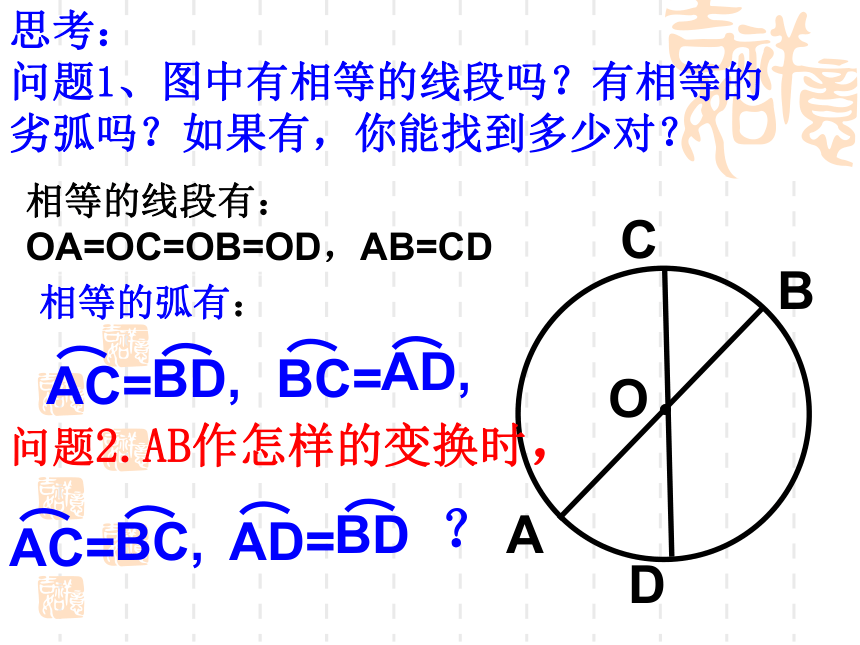
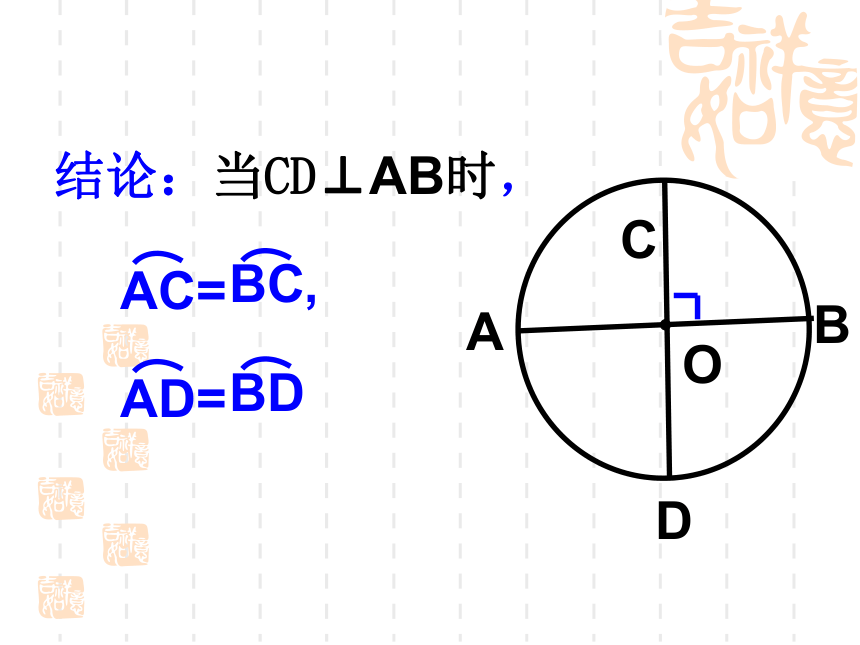
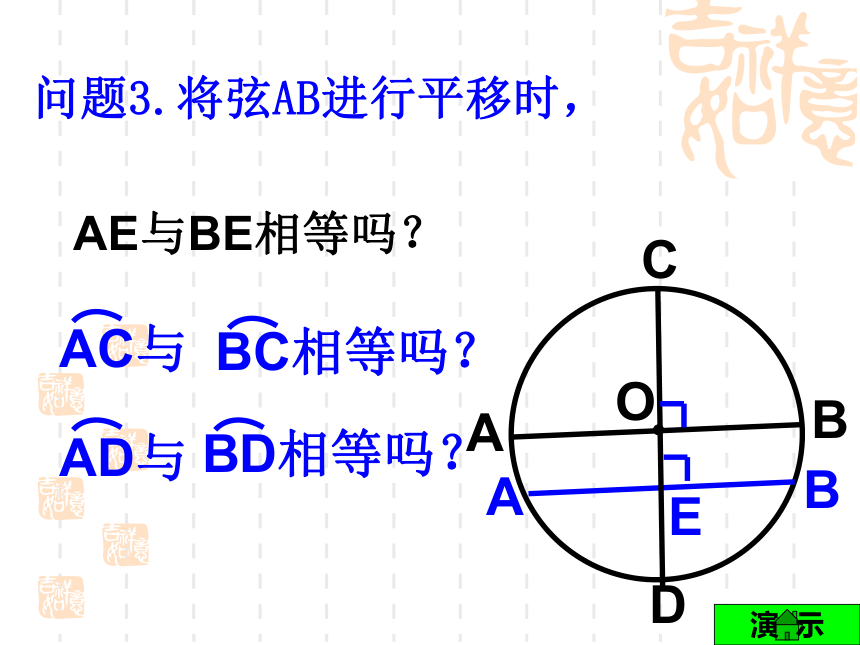
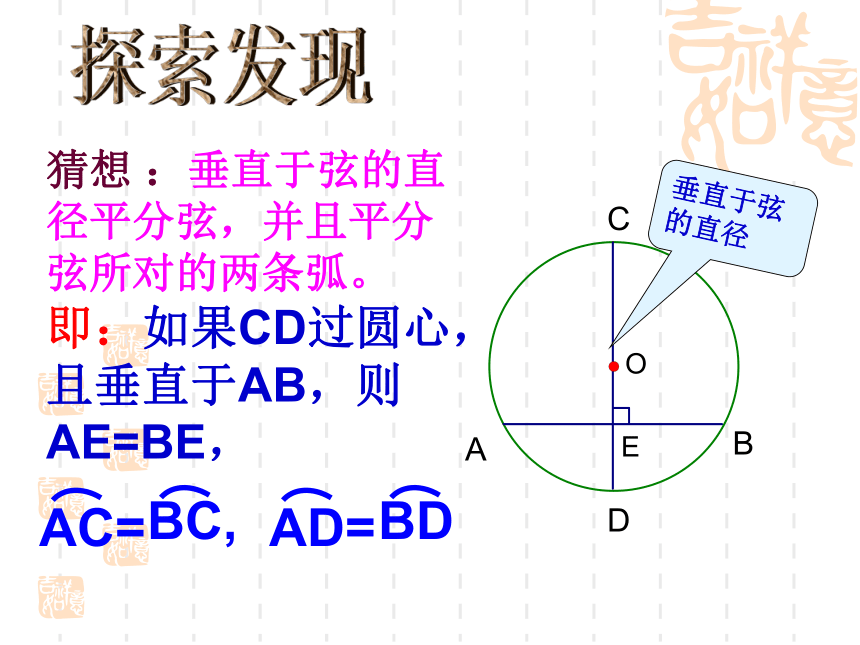
课件19张PPT。24.1.2 垂直于弦的直径(1) 由此你能得到圆的什么特性?可以发现:1、圆是轴对称图形。任何一条直径所在直线都是它的对称轴. 活动一 不借助任何工具,你能找到一张圆形纸片的圆心吗? ?2.圆是中心对称图形,对称中心是圆心。3.圆具有旋转不变性.ABCD思考: 问题1、图中有相等的线段吗?有相等的劣弧吗?如果有,你能找到多少对?O问题2.AB作怎样的变换时,?相等的线段有:OA=OC=OB=OD,AB=CD相等的弧有:CDABO结论:当CD⊥AB时,CDO问题3.将弦AB进行平移时,AB演 示EAE与BE相等吗?探索发现猜想 :垂直于弦的直径平分弦,并且平分弦所对的两条弧。
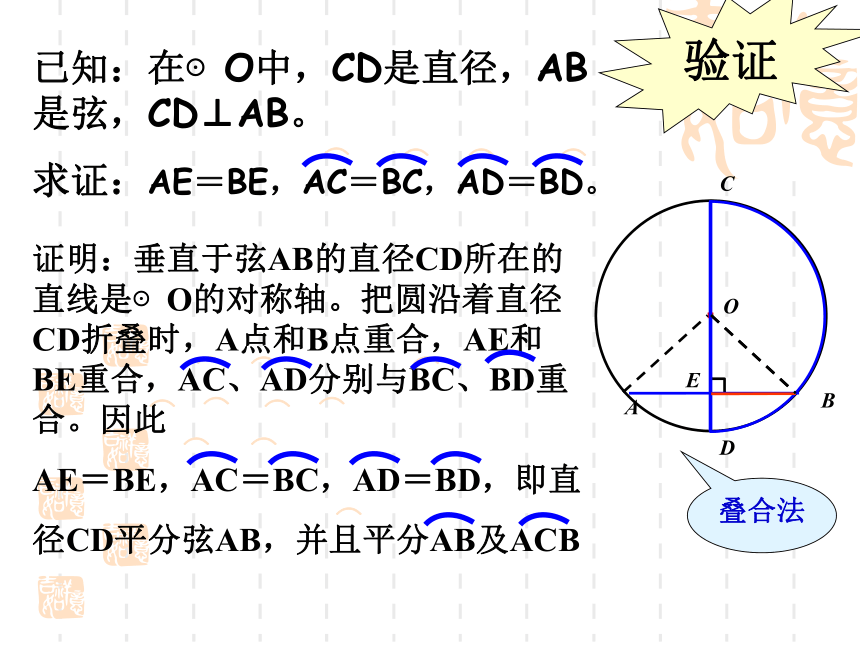
即:如果CD过圆心,且垂直于AB,则AE=BE,垂直于弦的直径验证⌒叠合法·OABCDE垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。
即:如果CD过圆心,且垂直于AB,则AE=BE,
结论:注意:过圆心和垂直于弦两个条件缺一不可进一步,我们还可以得到结论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。即:如果CD过圆心,且AE=BE则CD⊥AB,
想一想:为什么规定弦AB不是直径?下列图形是否具备垂径定理的条件?是不是是火眼金睛不是注意:定理中的两个条件(直径,垂直于弦)缺一不可!
轻松过关1、如图,AB是圆的弦,利用一个三角板,你能确定这条弦的中点吗?2、如图,点C是圆的任意一个点,利用一个三角板,你能画出一条弦AB,使点刚好是这条弦的中点吗?AB●C2.如图,在⊙O中,弦
AB的长为8cm,圆心O
到AB的距离为3cm,求⊙O的半径。·OABE3.若⊙O的半径为10cm,
OE=6cm,则AB= cm。轻松过关问题 :你知道赵州桥吗? 它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m,你能求出赵洲桥主桥拱的半径吗? 赵州桥主桥拱的半径是多少? 你能利用垂径定理解决求赵州桥拱半径的问题吗?大显身手37.4m7.2mABOCE解得:R≈27.9(m)在Rt△OAD中,由勾股定理,得即 R2=18.72+(R-7.2)2∴赵州桥的主桥拱半径约为27.9m.OA2=AD2+OD2AB=37.4,CD=7.2,OD=OC-CD=R-7.2在图中解:用 弧AB表示主桥拱,设弧AB 所在圆的圆心为O,半径为R.经过圆心O 作弦AB 的垂线OC,D为垂足,OC与AB 相交于点D,根据前面的结论,D 是AB 的中点,C是弧AB的中点,CD 就是拱高.
通过这节课的学习,
你有哪些收获?
能与大家一起分享吗?丰 收 园作业:习题24.1
1、8、10、更上层楼Upper formation building
即:如果CD过圆心,且垂直于AB,则AE=BE,垂直于弦的直径验证⌒叠合法·OABCDE垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。
即:如果CD过圆心,且垂直于AB,则AE=BE,
结论:注意:过圆心和垂直于弦两个条件缺一不可进一步,我们还可以得到结论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。即:如果CD过圆心,且AE=BE则CD⊥AB,
想一想:为什么规定弦AB不是直径?下列图形是否具备垂径定理的条件?是不是是火眼金睛不是注意:定理中的两个条件(直径,垂直于弦)缺一不可!
轻松过关1、如图,AB是圆的弦,利用一个三角板,你能确定这条弦的中点吗?2、如图,点C是圆的任意一个点,利用一个三角板,你能画出一条弦AB,使点刚好是这条弦的中点吗?AB●C2.如图,在⊙O中,弦
AB的长为8cm,圆心O
到AB的距离为3cm,求⊙O的半径。·OABE3.若⊙O的半径为10cm,
OE=6cm,则AB= cm。轻松过关问题 :你知道赵州桥吗? 它的主桥是圆弧形,它的跨度(弧所对的弦的长)为37.4m, 拱高(弧的中点到弦的距离)为7.2m,你能求出赵洲桥主桥拱的半径吗? 赵州桥主桥拱的半径是多少? 你能利用垂径定理解决求赵州桥拱半径的问题吗?大显身手37.4m7.2mABOCE解得:R≈27.9(m)在Rt△OAD中,由勾股定理,得即 R2=18.72+(R-7.2)2∴赵州桥的主桥拱半径约为27.9m.OA2=AD2+OD2AB=37.4,CD=7.2,OD=OC-CD=R-7.2在图中解:用 弧AB表示主桥拱,设弧AB 所在圆的圆心为O,半径为R.经过圆心O 作弦AB 的垂线OC,D为垂足,OC与AB 相交于点D,根据前面的结论,D 是AB 的中点,C是弧AB的中点,CD 就是拱高.
通过这节课的学习,
你有哪些收获?
能与大家一起分享吗?丰 收 园作业:习题24.1
1、8、10、更上层楼Upper formation building
同课章节目录
