4.3.2角的比较与运算,余角和补角
文档属性
| 名称 | 4.3.2角的比较与运算,余角和补角 |

|
|
| 格式 | rar | ||
| 文件大小 | 177.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-21 20:55:00 | ||
图片预览


文档简介
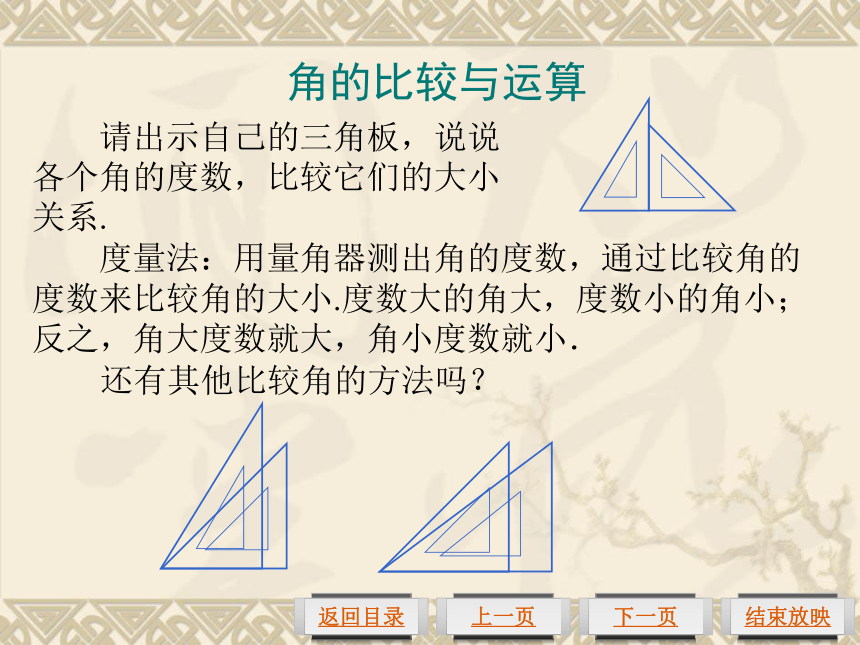
课件21张PPT。4.3.2 角的比较与运算,余角和补角单击页面即可演示 请出示自己的三角板,说说各个角的度数,比较它们的大小关系.还有其他比较角的方法吗? 度量法:用量角器测出角的度数,通过比较角的度数来比较角的大小.度数大的角大,度数小的角小;反之,角大度数就大,角小度数就小.角的比较与运算思考:
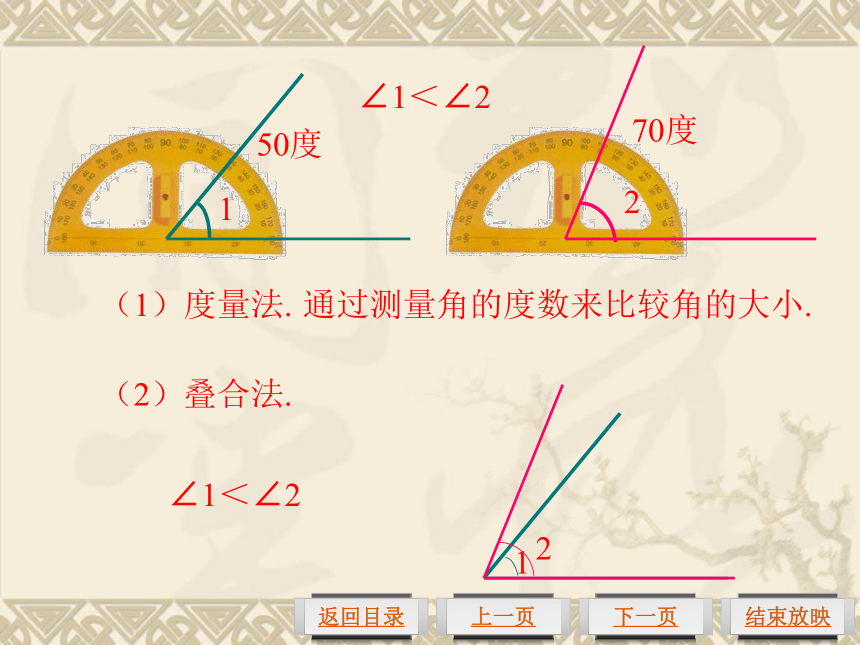
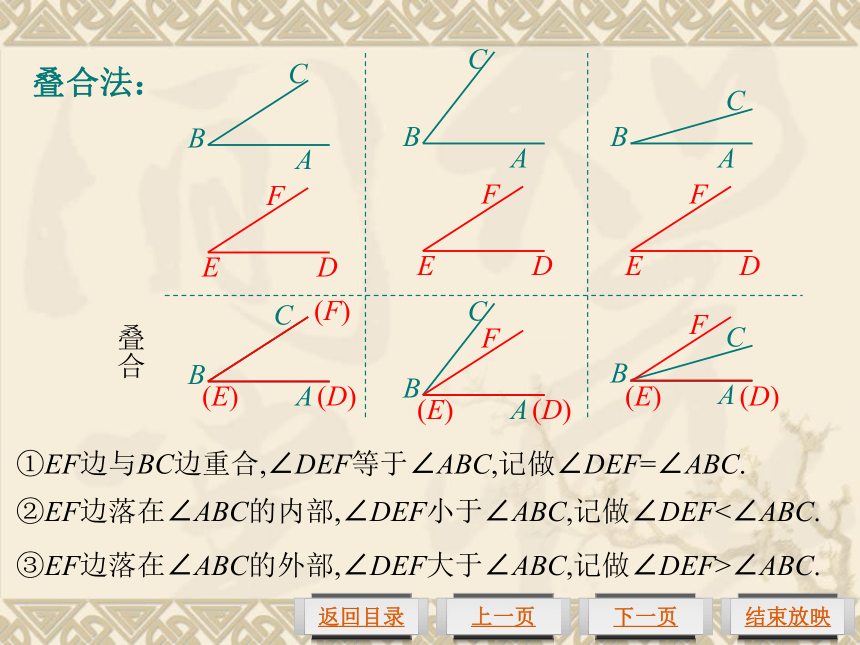
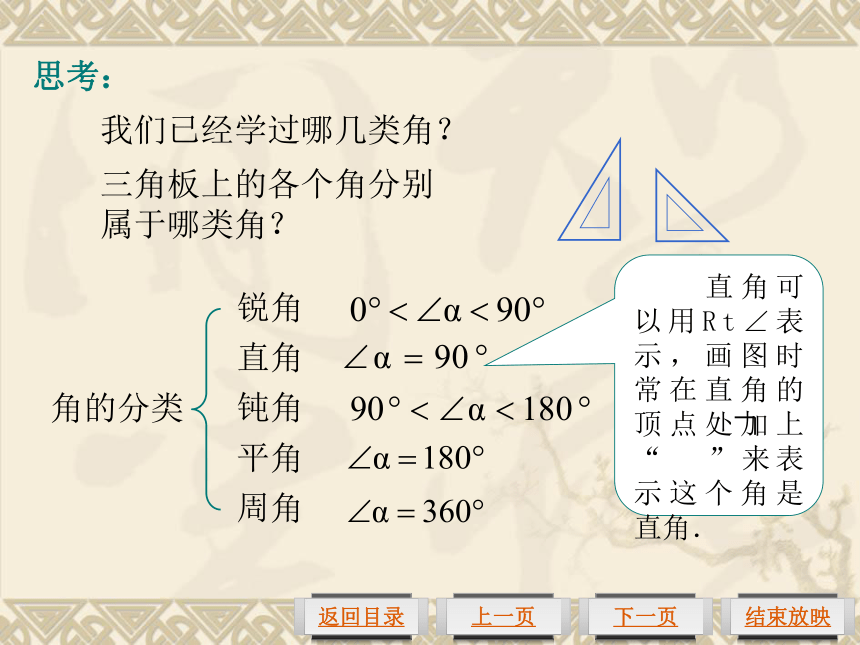
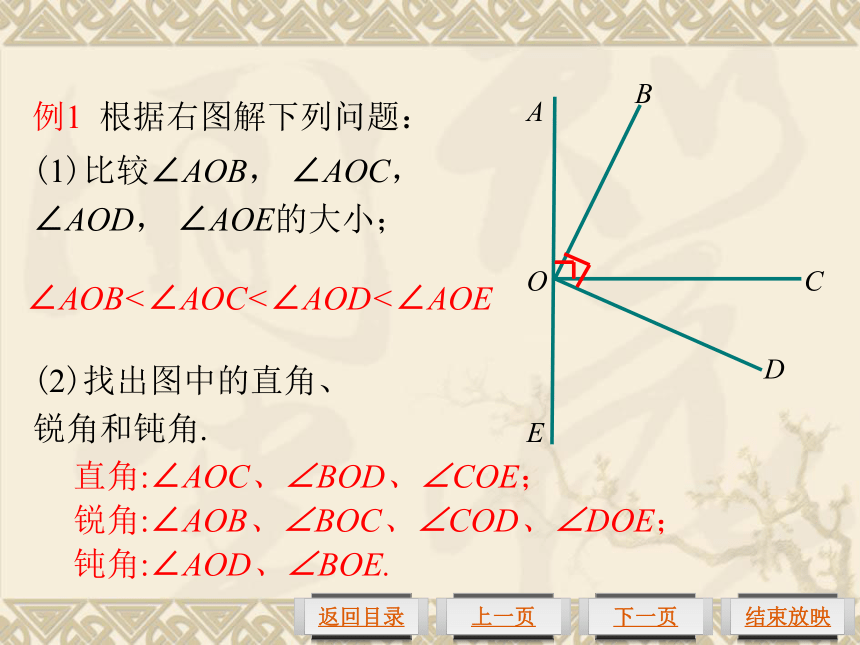
如何比较∠1和∠2的大小?1250度70度(1)度量法.通过测量角的度数来比较角的大小. (2)叠合法.∠1<∠2∠1<∠2叠合法:叠合①EF边与BC边重合,∠DEF等于∠ABC,记做∠DEF=∠ABC.②EF边落在∠ABC的内部,∠DEF小于∠ABC,记做∠DEF<∠ABC.③EF边落在∠ABC的外部,∠DEF大于∠ABC,记做∠DEF>∠ABC.思考:我们已经学过哪几类角?三角板上的各个角分别属于哪类角?角的分类锐角直角钝角平角周角例1 根据右图解下列问题:(1)比较∠AOB, ∠AOC, ∠AOD, ∠AOE的大小;(2)找出图中的直角、锐角和钝角.∠AOB<∠AOC<∠AOD<∠AOE直角:∠AOC、∠BOD、∠COE;
锐角:∠AOB、∠BOC、∠COD、∠DOE;
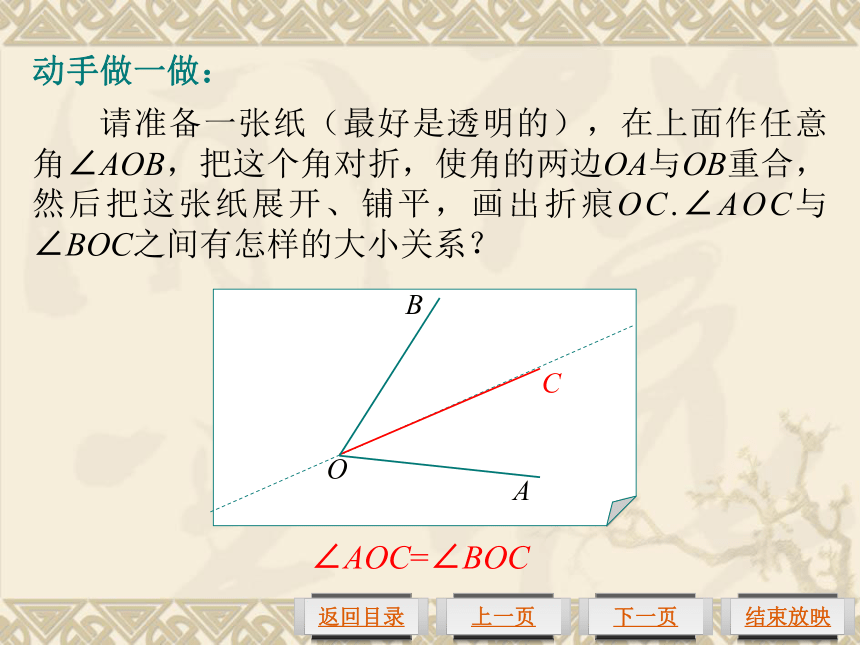
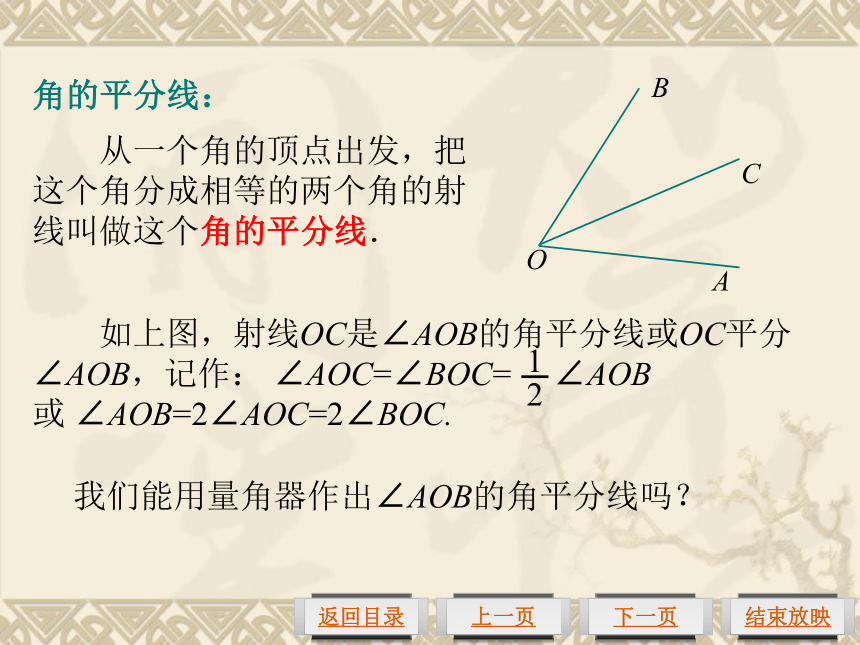
钝角:∠AOD、∠BOE.动手做一做: 请准备一张纸(最好是透明的),在上面作任意角∠AOB,把这个角对折,使角的两边OA与OB重合,然后把这张纸展开、铺平,画出折痕OC.∠AOC与∠BOC之间有怎样的大小关系?AOBC∠AOC=∠BOC角的平分线: 从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.我们能用量角器作出∠AOB的角平分线吗?例2(1)根据右图填空: ①∠DBA=∠DBC+ ; ②∠DBC=∠DBP- =
∠DBA- ; ③∠DBP+∠ABC-∠ABD= .(2)①如图,若∠ABC=90o,∠CBD=30o,你能求出哪些角的度数? ② 若在①的条件下再添上条件BP平分∠ABD,你还能求出哪些角的度数? ∠ABC∠PBC∠ABC∠PBC∠ABD =120°∠PBC =30°,∠PBA =60°, ∠PBD =60°.做一做:你知道下面这些角是怎样用三角板画出来的吗? 60°15°120°105°90°75°45°30°165°150°135°180°余角和补角1. 观察下面两个图形,回答问题.(1)射线ON把直角∠DOC分成了几个角?(2)∠3和∠4具有什么样的数量关系?两个角:∠3和∠4.∠3+∠4=90°ODC90°N34OCD2. 观察下面两个图形,回答问题.(1)射线OM 把平角∠AOB分成了几个角?(2)∠1和∠2具有什么样的数量关系?两个角:∠1和∠2.∠1+∠2=180°AOB180°AOBM12结论:
不论∠1、∠2、∠3、∠4的位置关系如何变化,只要大小不变,∠1与∠2的和永远是平角,∠3与∠4的和永远是直角.像这样具有特殊关系的角,我们分别叫它们互为补角和互为余角. 1.互为余角的定义:如果两个角的和等于90°(直角),就说这两个角互为余角,即其中一个角是另一个角的余角. 2.互为补角的定义:如果两个角的和等于180°(平角),就说这两个角互为补角,即其中一个角是另一个角的补角. 问题3:互为余角、互为补角的两个角是否一定有公共顶点? 问题1:以上定义中的“互为”是什么意思? 问题2:若∠1+∠2+∠3=180°,那么∠1、∠2、∠3互为补角吗? 思考:不互为补角不一定 ∠A是∠B的余(补)角,同样∠B是∠A的余
(补)角.练习:
1.如图,O是直线AB上一点,OC是∠AOB的平分线.
①∠AOD的补角是_______
②∠AOD的余角是_______
③∠DOB的补角是_______∠BOD∠COD∠AODADCOB 2.如下图,∠1与∠2互补,∠3与∠4互补,如果
∠1=∠3,那么∠2 =∠4相等吗?为什么? 分析:由 与 互补,可得 , 由 与 互补,可得 .∠1∠2 =180°- ∠1 ∠3∠4=180°-∠3∠4∠22143解:∵∠1=∠3 , ∴180°-∠1=180°-∠3,
即∠2 =∠4.结论:等角的补角相等.等角的余角相等.小结:1.互为补角、互为余角的定义.2.等角的补角相等;
等角的余角相等.同学们再见!
锐角:∠AOB、∠BOC、∠COD、∠DOE;
钝角:∠AOD、∠BOE.动手做一做: 请准备一张纸(最好是透明的),在上面作任意角∠AOB,把这个角对折,使角的两边OA与OB重合,然后把这张纸展开、铺平,画出折痕OC.∠AOC与∠BOC之间有怎样的大小关系?AOBC∠AOC=∠BOC角的平分线: 从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.我们能用量角器作出∠AOB的角平分线吗?例2(1)根据右图填空: ①∠DBA=∠DBC+ ; ②∠DBC=∠DBP- =
∠DBA- ; ③∠DBP+∠ABC-∠ABD= .(2)①如图,若∠ABC=90o,∠CBD=30o,你能求出哪些角的度数? ② 若在①的条件下再添上条件BP平分∠ABD,你还能求出哪些角的度数? ∠ABC∠PBC∠ABC∠PBC∠ABD =120°∠PBC =30°,∠PBA =60°, ∠PBD =60°.做一做:你知道下面这些角是怎样用三角板画出来的吗? 60°15°120°105°90°75°45°30°165°150°135°180°余角和补角1. 观察下面两个图形,回答问题.(1)射线ON把直角∠DOC分成了几个角?(2)∠3和∠4具有什么样的数量关系?两个角:∠3和∠4.∠3+∠4=90°ODC90°N34OCD2. 观察下面两个图形,回答问题.(1)射线OM 把平角∠AOB分成了几个角?(2)∠1和∠2具有什么样的数量关系?两个角:∠1和∠2.∠1+∠2=180°AOB180°AOBM12结论:
不论∠1、∠2、∠3、∠4的位置关系如何变化,只要大小不变,∠1与∠2的和永远是平角,∠3与∠4的和永远是直角.像这样具有特殊关系的角,我们分别叫它们互为补角和互为余角. 1.互为余角的定义:如果两个角的和等于90°(直角),就说这两个角互为余角,即其中一个角是另一个角的余角. 2.互为补角的定义:如果两个角的和等于180°(平角),就说这两个角互为补角,即其中一个角是另一个角的补角. 问题3:互为余角、互为补角的两个角是否一定有公共顶点? 问题1:以上定义中的“互为”是什么意思? 问题2:若∠1+∠2+∠3=180°,那么∠1、∠2、∠3互为补角吗? 思考:不互为补角不一定 ∠A是∠B的余(补)角,同样∠B是∠A的余
(补)角.练习:
1.如图,O是直线AB上一点,OC是∠AOB的平分线.
①∠AOD的补角是_______
②∠AOD的余角是_______
③∠DOB的补角是_______∠BOD∠COD∠AODADCOB 2.如下图,∠1与∠2互补,∠3与∠4互补,如果
∠1=∠3,那么∠2 =∠4相等吗?为什么? 分析:由 与 互补,可得 , 由 与 互补,可得 .∠1∠2 =180°- ∠1 ∠3∠4=180°-∠3∠4∠22143解:∵∠1=∠3 , ∴180°-∠1=180°-∠3,
即∠2 =∠4.结论:等角的补角相等.等角的余角相等.小结:1.互为补角、互为余角的定义.2.等角的补角相等;
等角的余角相等.同学们再见!
