逻辑关系与四种命题
图片预览









文档简介
课件32张PPT。四种命题教学目标:1.理解四种命题的概念,掌握
命题形式的表示.
2.培养学生简单推理的思维能力.
教学重点:四种命题的概念.
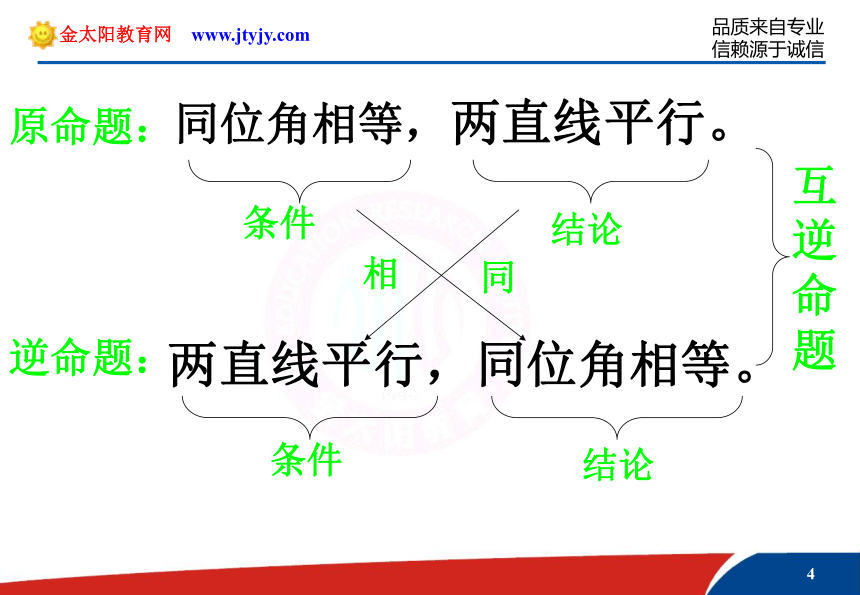
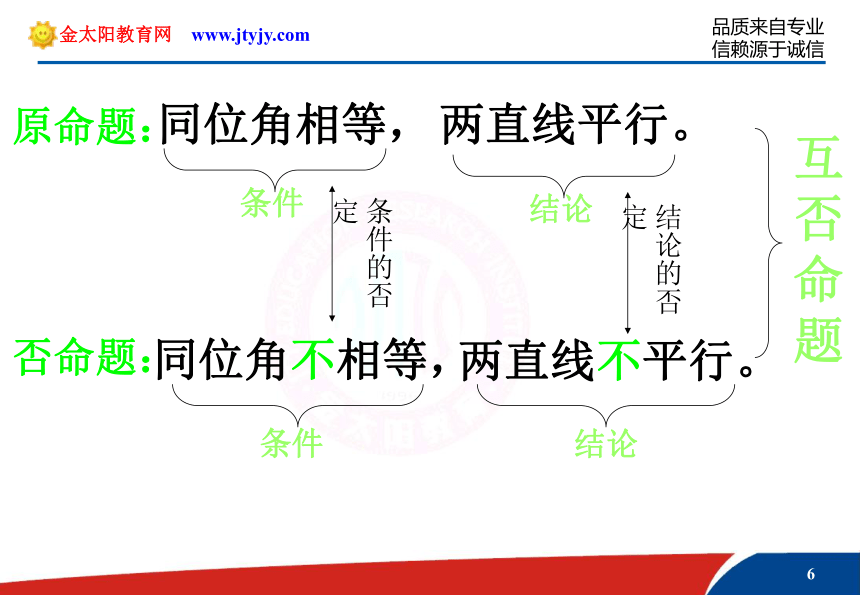
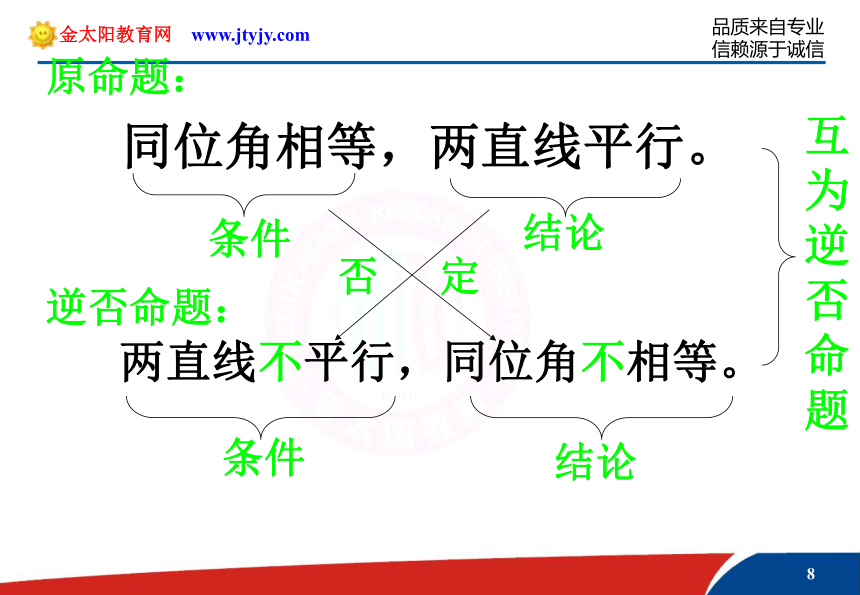
教学难点:由原命题写出另外三种命题.封面1、引例目的:通过实例,我们就可以形成感性认识,明确数学概念是从实际中抽象出来的。数学是有趣的!1、引例引例:互逆 同位角相等,两直线平行。两直线平行,同位角相等。引例同位角相等,两直线平行。两直线平行,同位角相等。条件结论结论条件相同 互逆命题原命题:逆命题:互为逆否分析同位角相等,两直线平行。同位角不相等,两直线不平行。引例:互否引例同位角相等,两直线平行。条件结论同位角不相等,两直线不平行。条件 结论条件的否定结论的否定互否命题原命题:否命题:互否分析同位角相等,两直线平行。两直线不平行,同位角不相等。引例:互为逆否引例同位角相等,两直线平行。两直线不平行,同位角不相等。条件结论结论条件否定 互为逆否命题原命题:逆否命题:互为逆否分析2、概括目的:通过实例,我们形成了感性认识,再进行概括、抽象,就可以形成新的数学概念。2、概括若f(x)是正弦函数,则f(x)是周期函数。若f(x)是周期函数,则f(x)是正弦函数。若f(x)不是正弦函数,则f(x)不是周期函数。若f(x)不是周期函数,则f(x)不是正弦函数。原命题:逆命题:否命题:逆否命题:以上四个命题原命题: 若p,则q.逆命题:否命题: 逆否命题:若q, 则p.若┐p ,则┐q。若┐q ,则┐p 。 由以上结论,要写出原命题的逆命题、否命题与逆否命题,关键是什么?
找出原命题的条件p与结论q。四个命题的总结概括3、例题目的:有了例题,我们就有了 “模仿”的依据,而“模仿” 则是“创新”的源头。3、例题例1 把下列命题改写成“若p则q”的形式,并写出它们的逆命题、否命题与逆否命题:(1) 对顶角相等;
(2) 负数的平方是正数。例1例题(1)对顶角相等。解:原命题可以写成:若两个角是对顶角,则这两个角相等。逆命题:若两个角相等,则这两个角是对顶角。逆否命题:若两个角不相等,则这两个角不是对顶角。否命题:若两个角不是对顶角,则这两个角不相等。(1)(2)负数的平方是正数。
解:原命题可以写成:若一个数是负数,则它的平方是正数。逆命题:若一个数的平方是正数,则这个数是负数。否命题:若一个数不是负数,则它的平方不是正数。逆否命题:若一个数的平方不是正数,则这个数不是负数。(2)4、练习目的:有了 “模仿”的依据,现在就请你开始“模仿” 吧,这样你就开始了发明创造的征程!4、练习 把下列命题改写成“若p则q”的形式,并写出它们的逆命题、否命题与逆否命题:课本P6 (1)
P8 3(1)(2)练习试一试,我能行!5、巩固练习目的:我们已开始了发明创造的征程,不要停下我们的脚步!5、巩固练习1、“若x2=1,则x=1”的否命题为 ( )
(A)若x2≠1,则x=1 (B)若x2=1,则x≠1
(C)若x2≠1,则x≠1 (B)若x≠1,则x2≠1
2、命题“两条对角线相等的四边形是矩形” 是命题“矩形是两条对角线相等的四边形”的(A)逆命题(B)否命题(C)逆否命题 ( )
3、命题“若a>b,则ac2>bc2”的逆否命题是 ( )
(A)若ac2>bc2 ,则a>b(B)若ac2>bc2 ,则a≤b
(C)若ac2≤bc2 ,则a≤b
(D)若a≤b ,则ac2≤bc2 巩固练习123CAC6、自主探究目的:很多奥秘等待我们去探索、研究,你还等什么,快来动手动脑吧!6、自主探究写出下列命题的逆命题,并判断它们的真假:
(1)若a<b,则a+c<b+c
(2)若a=0,则ab=0(1)逆命题:若a+c<b+c,则a<b真命题(2)逆命题: 若ab=0,则a=0假命题原命题为真,逆命题不一定为真逆命题真假自主探究写出下列命题的否命题,并判断它们的真假:
(1)若a<b,则a+c<b+c
(2)若a=0,则ab=0(1)否命题:若a≥b,则a+c≥b+c真命题(2)否命题: 若a≠0,则ab≠0假命题原命题为真,否命题不一定为真否命题真假自主探究写出下列命题的逆否命题,并判断它们的真假:
(1)若a<b,则a+c<b+c
(2)若a=0,则ab=0(1)逆否命题:若a+c≥b+c,则a≥b真命题(2)逆否命题:若ab≠0,则a≠0真命题原命题为真,逆否命题一定为真逆否命题真假自主探究7、课堂小结目的:我们这节课的主要内容是什么,快来想想吧!7、课堂小结1、四种命题的定义及形式;
2、写一个命题的逆命题、否命题、逆否命题的关键是分清原命题的条件和结论,可以先将原命题改写成“若p则q”的形式(写法不一定惟一),再写出其它三种命题(大前提不变);
3、会判断四种命题的真假。课堂小结:课堂小结8、达标检测目的:这节课的主要内容我们掌握了多少呢?让我们检测一下吧,堂堂清会提高我们的学习效率!8、达标检测1、下列说法中错误的一项是( )
A. 原命题为真,它的逆命题不一定为真
B. 原命题为真,它的否命题不一定为真
C. 一个命题的逆否命题为真,则这个命题不一定为真
D. 原命题为真,它的逆否命题一定为真C达标检测达标检测12、命题“到圆心的距离不等于半径的直线不是圆的切线”的逆否命题是:若一条直线是圆的切线,则它到圆心的距离等于半径。达标检测 23、写出下列命题的逆命题、否命题与逆否命题,同时指出它们的真假:
原命题:当c>0时,若a>b,则ac>bc达标检测解:逆命题:当c>0时,若ac>bc, 则a>b.否命题:当c>0时,若a≤b, 则ac≤bc.逆否命题:当c>0时,若ac≤bc, 则a≤b. 3真命题真命题真命题4.判断下列命题的真假:
(1) “菱形的对角线互相垂直平分”的逆否命题;
(2)“若xy≠0,则x≠0”的逆命题;真命题假命题达标检测 49、布置作业目的:作业是课堂教学的延伸与发展,你可要独立、认真地完成!9、布置作业研究性问题:请你课下写出一些命题及它们的逆命题、否命题、逆否命题,研究一下四种命题的真假关系有何必然联系。书面作业:课本:P8 A2; P30 A1 作业
命题形式的表示.
2.培养学生简单推理的思维能力.
教学重点:四种命题的概念.
教学难点:由原命题写出另外三种命题.封面1、引例目的:通过实例,我们就可以形成感性认识,明确数学概念是从实际中抽象出来的。数学是有趣的!1、引例引例:互逆 同位角相等,两直线平行。两直线平行,同位角相等。引例同位角相等,两直线平行。两直线平行,同位角相等。条件结论结论条件相同 互逆命题原命题:逆命题:互为逆否分析同位角相等,两直线平行。同位角不相等,两直线不平行。引例:互否引例同位角相等,两直线平行。条件结论同位角不相等,两直线不平行。条件 结论条件的否定结论的否定互否命题原命题:否命题:互否分析同位角相等,两直线平行。两直线不平行,同位角不相等。引例:互为逆否引例同位角相等,两直线平行。两直线不平行,同位角不相等。条件结论结论条件否定 互为逆否命题原命题:逆否命题:互为逆否分析2、概括目的:通过实例,我们形成了感性认识,再进行概括、抽象,就可以形成新的数学概念。2、概括若f(x)是正弦函数,则f(x)是周期函数。若f(x)是周期函数,则f(x)是正弦函数。若f(x)不是正弦函数,则f(x)不是周期函数。若f(x)不是周期函数,则f(x)不是正弦函数。原命题:逆命题:否命题:逆否命题:以上四个命题原命题: 若p,则q.逆命题:否命题: 逆否命题:若q, 则p.若┐p ,则┐q。若┐q ,则┐p 。 由以上结论,要写出原命题的逆命题、否命题与逆否命题,关键是什么?
找出原命题的条件p与结论q。四个命题的总结概括3、例题目的:有了例题,我们就有了 “模仿”的依据,而“模仿” 则是“创新”的源头。3、例题例1 把下列命题改写成“若p则q”的形式,并写出它们的逆命题、否命题与逆否命题:(1) 对顶角相等;
(2) 负数的平方是正数。例1例题(1)对顶角相等。解:原命题可以写成:若两个角是对顶角,则这两个角相等。逆命题:若两个角相等,则这两个角是对顶角。逆否命题:若两个角不相等,则这两个角不是对顶角。否命题:若两个角不是对顶角,则这两个角不相等。(1)(2)负数的平方是正数。
解:原命题可以写成:若一个数是负数,则它的平方是正数。逆命题:若一个数的平方是正数,则这个数是负数。否命题:若一个数不是负数,则它的平方不是正数。逆否命题:若一个数的平方不是正数,则这个数不是负数。(2)4、练习目的:有了 “模仿”的依据,现在就请你开始“模仿” 吧,这样你就开始了发明创造的征程!4、练习 把下列命题改写成“若p则q”的形式,并写出它们的逆命题、否命题与逆否命题:课本P6 (1)
P8 3(1)(2)练习试一试,我能行!5、巩固练习目的:我们已开始了发明创造的征程,不要停下我们的脚步!5、巩固练习1、“若x2=1,则x=1”的否命题为 ( )
(A)若x2≠1,则x=1 (B)若x2=1,则x≠1
(C)若x2≠1,则x≠1 (B)若x≠1,则x2≠1
2、命题“两条对角线相等的四边形是矩形” 是命题“矩形是两条对角线相等的四边形”的(A)逆命题(B)否命题(C)逆否命题 ( )
3、命题“若a>b,则ac2>bc2”的逆否命题是 ( )
(A)若ac2>bc2 ,则a>b(B)若ac2>bc2 ,则a≤b
(C)若ac2≤bc2 ,则a≤b
(D)若a≤b ,则ac2≤bc2 巩固练习123CAC6、自主探究目的:很多奥秘等待我们去探索、研究,你还等什么,快来动手动脑吧!6、自主探究写出下列命题的逆命题,并判断它们的真假:
(1)若a<b,则a+c<b+c
(2)若a=0,则ab=0(1)逆命题:若a+c<b+c,则a<b真命题(2)逆命题: 若ab=0,则a=0假命题原命题为真,逆命题不一定为真逆命题真假自主探究写出下列命题的否命题,并判断它们的真假:
(1)若a<b,则a+c<b+c
(2)若a=0,则ab=0(1)否命题:若a≥b,则a+c≥b+c真命题(2)否命题: 若a≠0,则ab≠0假命题原命题为真,否命题不一定为真否命题真假自主探究写出下列命题的逆否命题,并判断它们的真假:
(1)若a<b,则a+c<b+c
(2)若a=0,则ab=0(1)逆否命题:若a+c≥b+c,则a≥b真命题(2)逆否命题:若ab≠0,则a≠0真命题原命题为真,逆否命题一定为真逆否命题真假自主探究7、课堂小结目的:我们这节课的主要内容是什么,快来想想吧!7、课堂小结1、四种命题的定义及形式;
2、写一个命题的逆命题、否命题、逆否命题的关键是分清原命题的条件和结论,可以先将原命题改写成“若p则q”的形式(写法不一定惟一),再写出其它三种命题(大前提不变);
3、会判断四种命题的真假。课堂小结:课堂小结8、达标检测目的:这节课的主要内容我们掌握了多少呢?让我们检测一下吧,堂堂清会提高我们的学习效率!8、达标检测1、下列说法中错误的一项是( )
A. 原命题为真,它的逆命题不一定为真
B. 原命题为真,它的否命题不一定为真
C. 一个命题的逆否命题为真,则这个命题不一定为真
D. 原命题为真,它的逆否命题一定为真C达标检测达标检测12、命题“到圆心的距离不等于半径的直线不是圆的切线”的逆否命题是:若一条直线是圆的切线,则它到圆心的距离等于半径。达标检测 23、写出下列命题的逆命题、否命题与逆否命题,同时指出它们的真假:
原命题:当c>0时,若a>b,则ac>bc达标检测解:逆命题:当c>0时,若ac>bc, 则a>b.否命题:当c>0时,若a≤b, 则ac≤bc.逆否命题:当c>0时,若ac≤bc, 则a≤b. 3真命题真命题真命题4.判断下列命题的真假:
(1) “菱形的对角线互相垂直平分”的逆否命题;
(2)“若xy≠0,则x≠0”的逆命题;真命题假命题达标检测 49、布置作业目的:作业是课堂教学的延伸与发展,你可要独立、认真地完成!9、布置作业研究性问题:请你课下写出一些命题及它们的逆命题、否命题、逆否命题,研究一下四种命题的真假关系有何必然联系。书面作业:课本:P8 A2; P30 A1 作业
