函数奇偶性
图片预览

文档简介
1.3.2 函数的奇偶性
巨野县实验中学 刘士臣
学习目标:掌握奇、偶函数的概念和意义,会证明一个函数是奇函数或偶函数。
学习重点:判断一个函数的奇偶性。
学习难点:函数奇偶性的证明。
学习过程:
一、大自然的美
二、新知探究
探究一
①如图所示,观察下列函数的图象,这两个函数图象有什么共同特征?
②那么,如何利用函数的解析式描述函数的图象关于轴对称呢?填写表1和表2,你发现这两个函数的解析式具有什么共同特征?
表1
... ...
... ...
由表可知:,,
实际上,对于定义域内任意的一个都有 ,即
表2
... ...
... ...
由表可知:,
实际上,对于定义域内任意的一个,都有 ,即
偶函数定义:
思考?1、偶函数的图象有什么特征?在对称区间上函数的单调性有何关系?
2、函数,是偶函数吗?
3、偶函数的定义域有什么特征?
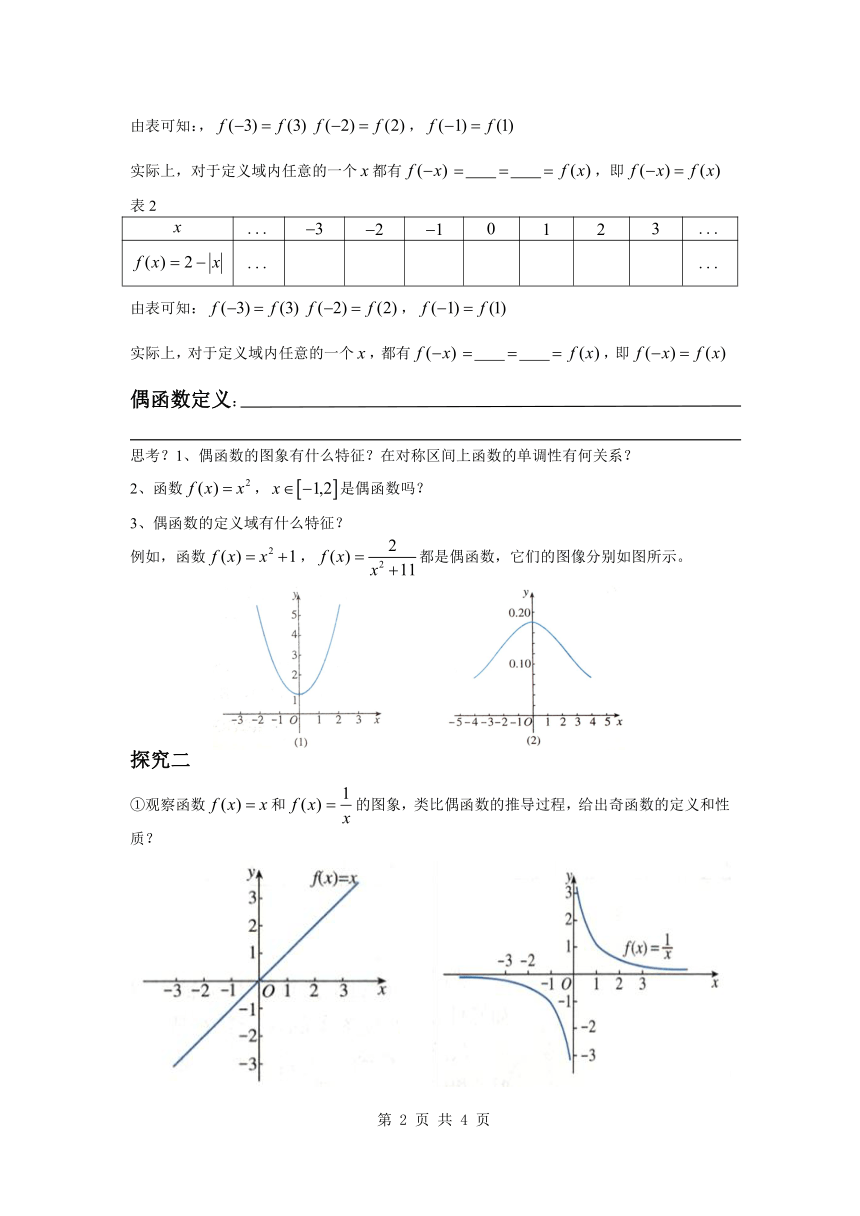
例如,函数,都是偶函数,它们的图像分别如图所示。
探究二
①观察函数和的图象,类比偶函数的推导过程,给出奇函数的定义和性质?
表3
... ...
... ...
由表可知:,,
实际上,对于定义域内任意的一个,都有 ,即
表4
... ...
... ...
由表可知:,
实际上,对于定义域内任意的一个,都有 ,即
奇函数的定义:
思考?(1)奇函数的图象有什么特征?在对称区间上函数的单调性有何关系?
(2)奇函数的定义域有什么特征?
注意:关于奇函数、偶函数定义的几点说明:
三、典例精析
例1(1)判断函数的奇偶性。
(2)如图所示为函数图象的一部分,
你能根据的奇偶性画出它在轴左边的图像吗?
小结:(1)用定义判断函数奇偶性的步骤:
(2)奇偶函数图象的性质可用于:
变式、判断下列函数的奇偶性:
(1);(2) ; (3) ; (4).
探究三:
猜想:有没有既是奇函数,又是偶函数的函数 有没有既不是奇函数,又不是偶函数的函数? 试举例说明!
函数的分类:
四、课堂小结:
五、课堂练习:
1、判断下列函数的奇偶性:
① ② ③
④ ⑤ ⑥
2、如果定义在区间上的函数为奇函数,则=_____
3、己知,若,则__ _
4、己知函数是偶函数,且在(-∞,0)上是增函数,则y=f(x)在(0,+∞)上是( )
A. 增函数 B. 减函数 C. 不是单调函数 D. 单调性不确定
5、 已知是偶函数,是奇函数,试将下图补充完整。
六、作业:教材,习题1.3A组6,B组3.
七、课堂反思:
0
x
y
第 1 页 共 4 页
巨野县实验中学 刘士臣
学习目标:掌握奇、偶函数的概念和意义,会证明一个函数是奇函数或偶函数。
学习重点:判断一个函数的奇偶性。
学习难点:函数奇偶性的证明。
学习过程:
一、大自然的美
二、新知探究
探究一
①如图所示,观察下列函数的图象,这两个函数图象有什么共同特征?
②那么,如何利用函数的解析式描述函数的图象关于轴对称呢?填写表1和表2,你发现这两个函数的解析式具有什么共同特征?
表1
... ...
... ...
由表可知:,,
实际上,对于定义域内任意的一个都有 ,即
表2
... ...
... ...
由表可知:,
实际上,对于定义域内任意的一个,都有 ,即
偶函数定义:
思考?1、偶函数的图象有什么特征?在对称区间上函数的单调性有何关系?
2、函数,是偶函数吗?
3、偶函数的定义域有什么特征?
例如,函数,都是偶函数,它们的图像分别如图所示。
探究二
①观察函数和的图象,类比偶函数的推导过程,给出奇函数的定义和性质?
表3
... ...
... ...
由表可知:,,
实际上,对于定义域内任意的一个,都有 ,即
表4
... ...
... ...
由表可知:,
实际上,对于定义域内任意的一个,都有 ,即
奇函数的定义:
思考?(1)奇函数的图象有什么特征?在对称区间上函数的单调性有何关系?
(2)奇函数的定义域有什么特征?
注意:关于奇函数、偶函数定义的几点说明:
三、典例精析
例1(1)判断函数的奇偶性。
(2)如图所示为函数图象的一部分,
你能根据的奇偶性画出它在轴左边的图像吗?
小结:(1)用定义判断函数奇偶性的步骤:
(2)奇偶函数图象的性质可用于:
变式、判断下列函数的奇偶性:
(1);(2) ; (3) ; (4).
探究三:
猜想:有没有既是奇函数,又是偶函数的函数 有没有既不是奇函数,又不是偶函数的函数? 试举例说明!
函数的分类:
四、课堂小结:
五、课堂练习:
1、判断下列函数的奇偶性:
① ② ③
④ ⑤ ⑥
2、如果定义在区间上的函数为奇函数,则=_____
3、己知,若,则__ _
4、己知函数是偶函数,且在(-∞,0)上是增函数,则y=f(x)在(0,+∞)上是( )
A. 增函数 B. 减函数 C. 不是单调函数 D. 单调性不确定
5、 已知是偶函数,是奇函数,试将下图补充完整。
六、作业:教材,习题1.3A组6,B组3.
七、课堂反思:
0
x
y
第 1 页 共 4 页
