相似三角形的性质
图片预览






文档简介
课件30张PPT。相似三角形的性质回顾复习:(1)什么叫相似三角形?
对应角相等、对应边成比例的三角形,叫做相似三角形.(2)如何识别两个三角形相似?①两个角对应相等;
②两边对应成比例且夹角相等;
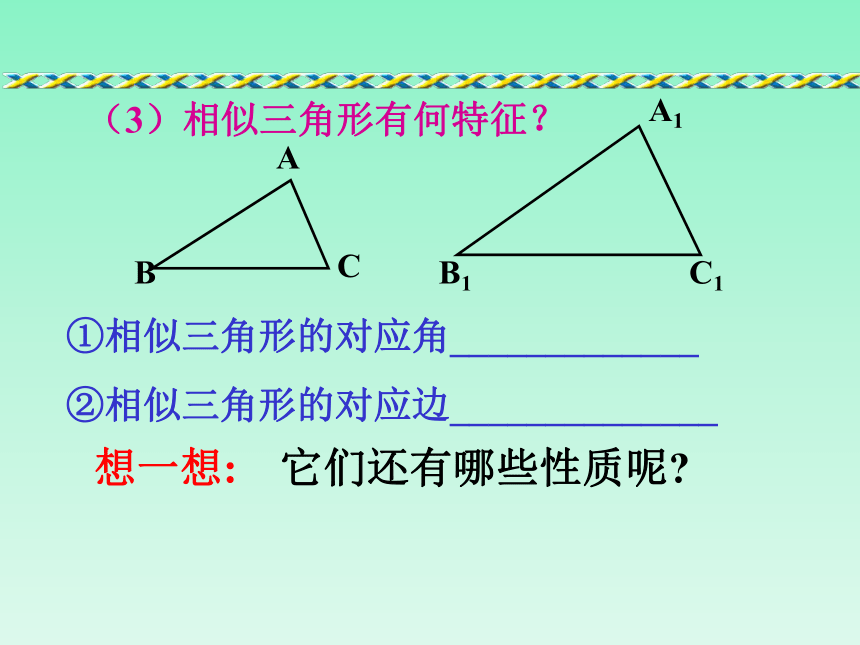
③三边对应成比例.ABCA1B1C1①相似三角形的对应角_____________
②相似三角形的对应边______________ 想一想: 它们还有哪些性质呢?(3)相似三角形有何特征?一个三角形有三条重要线段:
________________如果两个三角形相似,
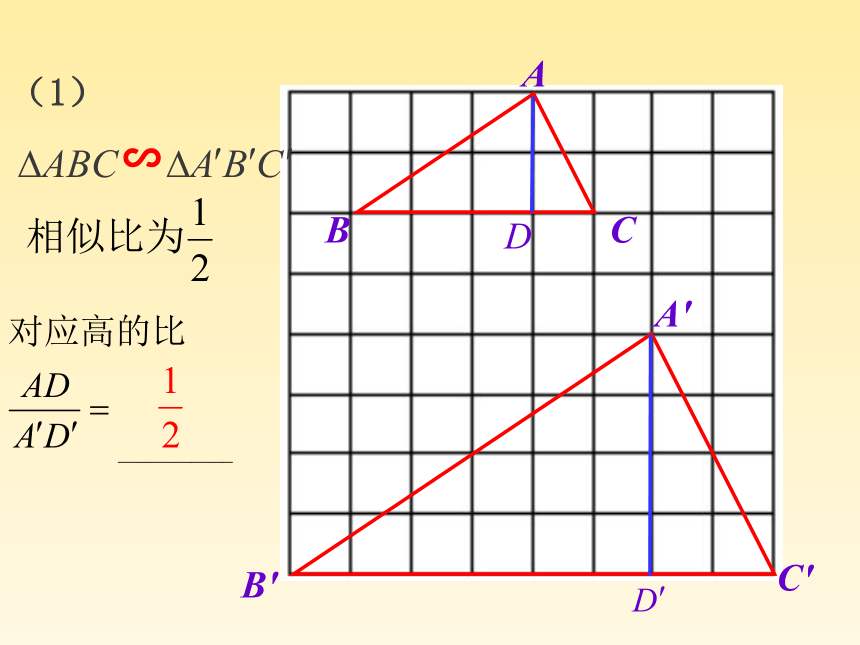
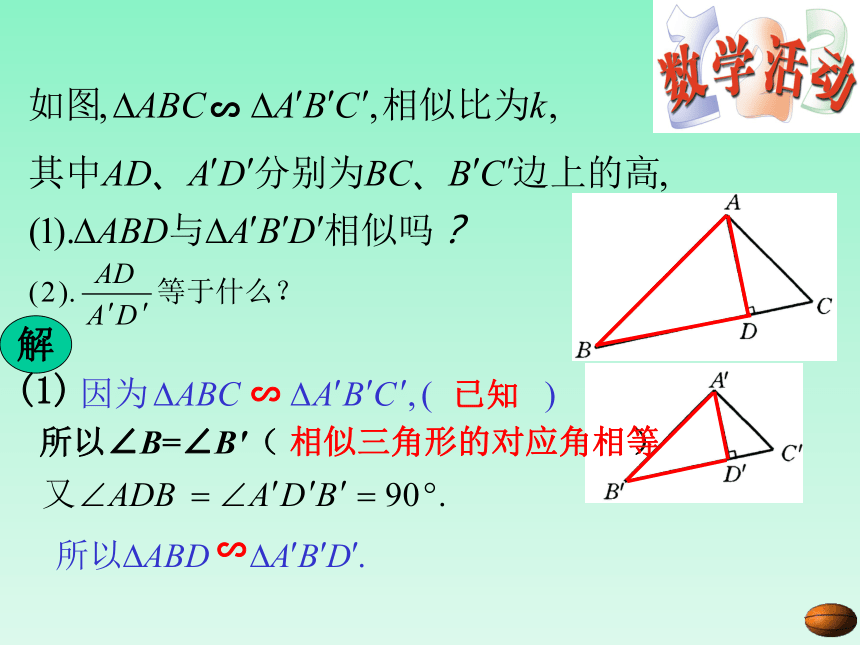
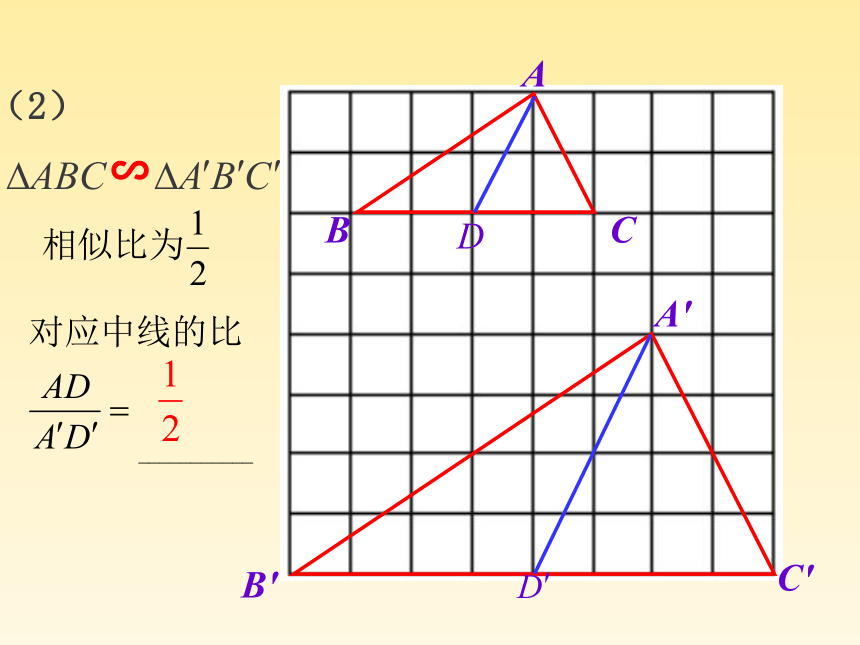
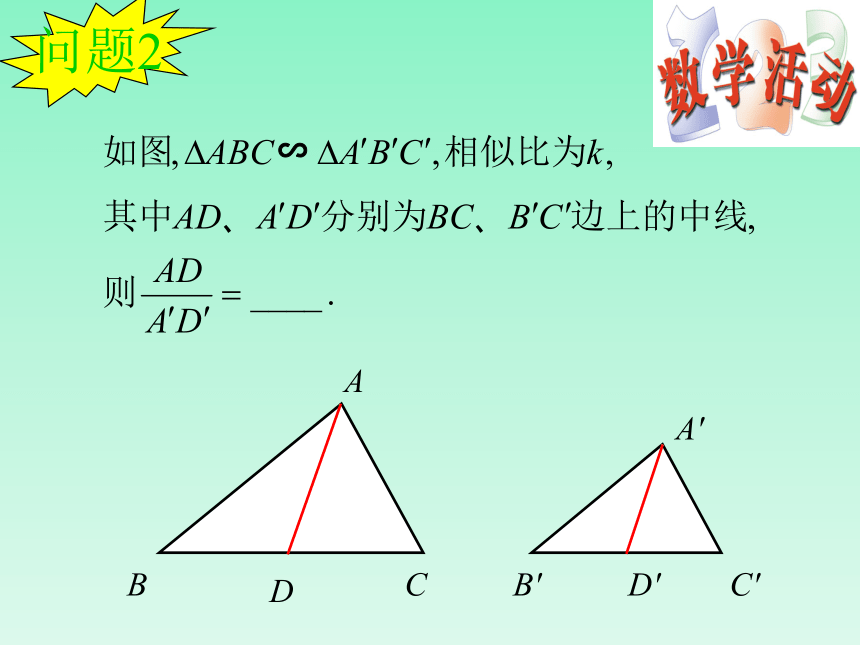
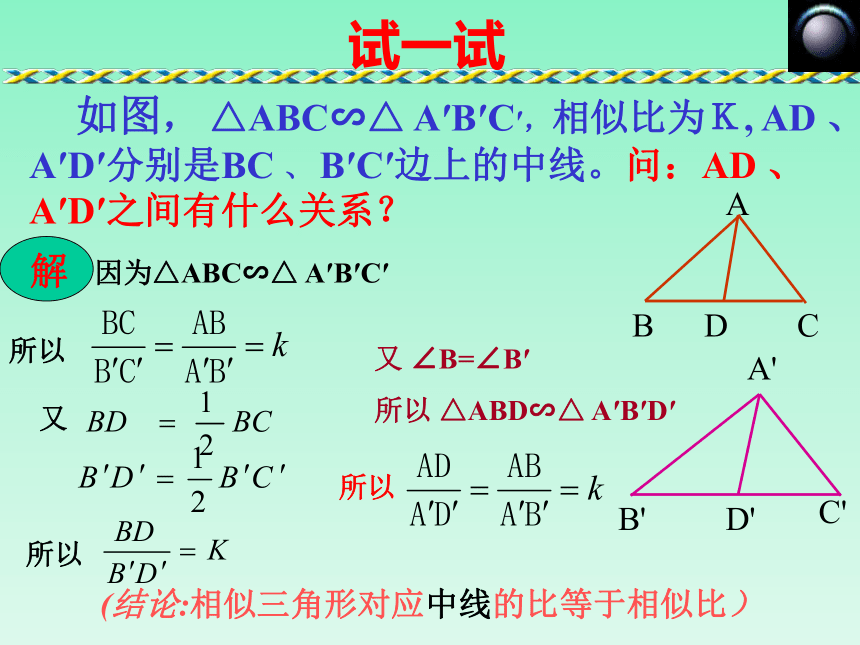
那么这些对应线段有什么关系呢?情境引入高、中线、角平分线(1)D'C'B'A'DCBA∽问题1∽已知所以∠B=∠B′( )相似三角形的对应角相等 解(1)∽所以∽结论:相似三角形对应高的比等于相似比.解(2)D'C'B'A'DCBA∽问题2试一试 如图, △ABC∽△ A′B′C′,相似比为K, AD 、 A′D′分别是BC 、 B′C′边上的中线。问:AD 、 A′D′之间有什么关系?
D'C'B'A'DCBA 因为△ABC∽△ A′B′C′
解所以又又 ∠B=∠B′
所以 △ABD∽△ A′B′D′所以(结论:相似三角形对应中线的比等于相似比)所以D'C'B'A'DCBA∽结论:相似三角形对应中线的比等于相似比.猜一猜(3)A′C′B′CBAE′E∽结论:相似三角形对应角的角平分线的比等于相似比.大胆
猜想对应高的比
对应中线的比
对应角平分线的比 都等于相似比.相似三角形的性质1.相似三角形对应边的比为 ,那么相似比为_________,对应角的角平分线的比为______.2∶32∶32.两个相似三角形的相似比为0.25, 则对应高的比为_________,对应角的角平分线的比为_________. 0.250.253.两个相似三角形对应中线的比为 ,
则相似比为______,对应高的比为______ .2∶3练一练两个相似三角形的周长比
会等于相似比吗?问题4图中(1)(2)(3)分别是边长为1、2、3的等边三角形,它们都相似吗?(1)(2)(3)123(1)与(2)的相似比=______,
(1)与(2)的周长比=______
(2)与(3)的相似比=______,
(2)与(3)的周长比=______1∶ 2(都相似)3∶ 62∶ 36∶ 9=1∶ 2=2∶ 3 如图,△ABC∽△A1B1C1,求证:已知:相似比是k,证明:结论:相似三角形的周长比等于 相似比.对应高的比
对应中线的比
对应角平分线的比
相
似
三
角
形都等于相似比.周长的比两个相似三角形的面积
之间有什么关系呢?问题51231∶ 2(1)(2)(3)(1)与(2)的相似比=______,
(1)与(2)的面积比=______
(2)与(3)的相似比=______,
(2)与(3)的面积比=______1∶ 42∶ 34∶ 9∽证明:=k2=k2结论:
相似三角形面积的比等于相似比的平方.对应高的比
对应中线的比
对应角平分线的比
周长的比 相
似
三
角
形都等于相似比.面积的比等于相似比的平方1.如果两个三角形相似,相似比为3∶5,则对应角的角平分线的比等于______.2.相似三角形对应边的比为0.4,
那么相似比为_______,
对应角的角平分线的比为______,
周长的比为_________,
面积的比为_________.3∶5 0.40.40.40.16练一练3.如图,在正方形网格上有△A1B1C1和△A2B2C2 ,这两个三角形相似吗?
如果相似,求出△A1B1C1和△A2B2C2的面积比.2 : 1解:相似.因为相似比是
4 : 1所以面积比是 (1)△ADE与△ABC相似吗?如果相似, 求它们的相似比. ABCDE1∶4 (2) △ADE的周长︰△ABC的周长=_______. 1∶4 例1、如图,DE∥BC, DE = 1, BC = 4, 1、相似三角形对应边成____,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
相似比的平方相似多边形也有同样的结论比例相等相似比相似比课堂小结课后作业 1、如图,在 ABCD中,E是BC上一点,AC与DE相交于F,若AE:EB=1:2,求?AEF与?CDF的相似比。若?AEF的面积为5平方厘米,求?CDF的面积。2、如图,△ABC是一块锐角
三角形余料,边BC=120毫米,
高AD=80毫米,要把它加工成正
方形零件,使正方形的一边在BC上,
其余两个顶点分别在AB、AC上,
这个正方形零件的边长是多少?~谢谢~
对应角相等、对应边成比例的三角形,叫做相似三角形.(2)如何识别两个三角形相似?①两个角对应相等;
②两边对应成比例且夹角相等;
③三边对应成比例.ABCA1B1C1①相似三角形的对应角_____________
②相似三角形的对应边______________ 想一想: 它们还有哪些性质呢?(3)相似三角形有何特征?一个三角形有三条重要线段:
________________如果两个三角形相似,
那么这些对应线段有什么关系呢?情境引入高、中线、角平分线(1)D'C'B'A'DCBA∽问题1∽已知所以∠B=∠B′( )相似三角形的对应角相等 解(1)∽所以∽结论:相似三角形对应高的比等于相似比.解(2)D'C'B'A'DCBA∽问题2试一试 如图, △ABC∽△ A′B′C′,相似比为K, AD 、 A′D′分别是BC 、 B′C′边上的中线。问:AD 、 A′D′之间有什么关系?
D'C'B'A'DCBA 因为△ABC∽△ A′B′C′
解所以又又 ∠B=∠B′
所以 △ABD∽△ A′B′D′所以(结论:相似三角形对应中线的比等于相似比)所以D'C'B'A'DCBA∽结论:相似三角形对应中线的比等于相似比.猜一猜(3)A′C′B′CBAE′E∽结论:相似三角形对应角的角平分线的比等于相似比.大胆
猜想对应高的比
对应中线的比
对应角平分线的比 都等于相似比.相似三角形的性质1.相似三角形对应边的比为 ,那么相似比为_________,对应角的角平分线的比为______.2∶32∶32.两个相似三角形的相似比为0.25, 则对应高的比为_________,对应角的角平分线的比为_________. 0.250.253.两个相似三角形对应中线的比为 ,
则相似比为______,对应高的比为______ .2∶3练一练两个相似三角形的周长比
会等于相似比吗?问题4图中(1)(2)(3)分别是边长为1、2、3的等边三角形,它们都相似吗?(1)(2)(3)123(1)与(2)的相似比=______,
(1)与(2)的周长比=______
(2)与(3)的相似比=______,
(2)与(3)的周长比=______1∶ 2(都相似)3∶ 62∶ 36∶ 9=1∶ 2=2∶ 3 如图,△ABC∽△A1B1C1,求证:已知:相似比是k,证明:结论:相似三角形的周长比等于 相似比.对应高的比
对应中线的比
对应角平分线的比
相
似
三
角
形都等于相似比.周长的比两个相似三角形的面积
之间有什么关系呢?问题51231∶ 2(1)(2)(3)(1)与(2)的相似比=______,
(1)与(2)的面积比=______
(2)与(3)的相似比=______,
(2)与(3)的面积比=______1∶ 42∶ 34∶ 9∽证明:=k2=k2结论:
相似三角形面积的比等于相似比的平方.对应高的比
对应中线的比
对应角平分线的比
周长的比 相
似
三
角
形都等于相似比.面积的比等于相似比的平方1.如果两个三角形相似,相似比为3∶5,则对应角的角平分线的比等于______.2.相似三角形对应边的比为0.4,
那么相似比为_______,
对应角的角平分线的比为______,
周长的比为_________,
面积的比为_________.3∶5 0.40.40.40.16练一练3.如图,在正方形网格上有△A1B1C1和△A2B2C2 ,这两个三角形相似吗?
如果相似,求出△A1B1C1和△A2B2C2的面积比.2 : 1解:相似.因为相似比是
4 : 1所以面积比是 (1)△ADE与△ABC相似吗?如果相似, 求它们的相似比. ABCDE1∶4 (2) △ADE的周长︰△ABC的周长=_______. 1∶4 例1、如图,DE∥BC, DE = 1, BC = 4, 1、相似三角形对应边成____,对应角______.
2、相似三角形对应边上的高、对应边上的中线、
对应角平分线的比都等于________.
3、相似三角形周长的比等于________,
相似三角形面积的比等于______________.
相似比的平方相似多边形也有同样的结论比例相等相似比相似比课堂小结课后作业 1、如图,在 ABCD中,E是BC上一点,AC与DE相交于F,若AE:EB=1:2,求?AEF与?CDF的相似比。若?AEF的面积为5平方厘米,求?CDF的面积。2、如图,△ABC是一块锐角
三角形余料,边BC=120毫米,
高AD=80毫米,要把它加工成正
方形零件,使正方形的一边在BC上,
其余两个顶点分别在AB、AC上,
这个正方形零件的边长是多少?~谢谢~
