基本不等式
图片预览




文档简介
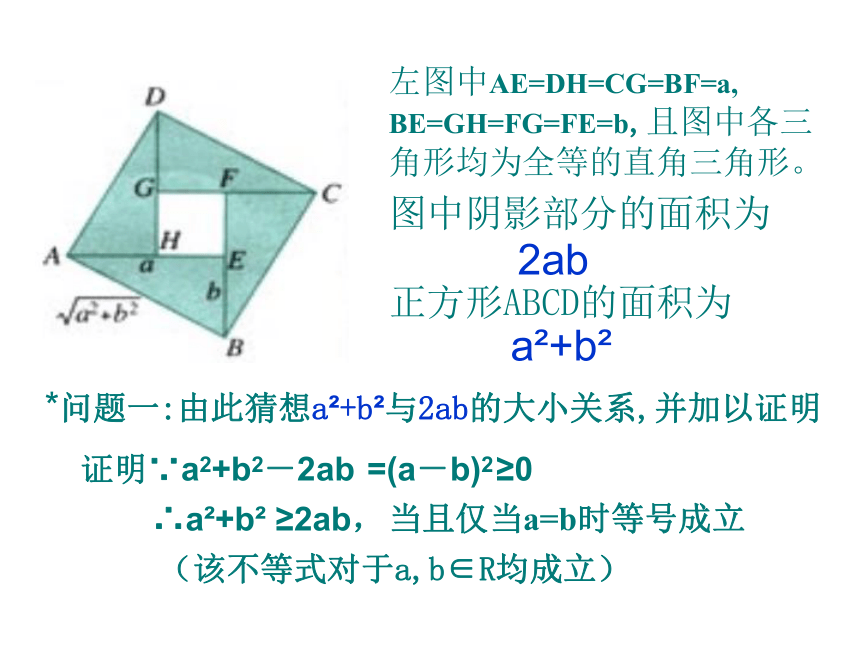
课件14张PPT。基本不等式图中阴影部分的面积为正方形ABCD的面积为a2+b22ab*问题一:由此猜想a2+b2与2ab的大小关系,并加以证明证明∵a2+b2-2ab=(a-b)2≥0∴a2+b2 ≥2ab,(该不等式对于a,b∈R均成立)左图中AE=DH=CG=BF=a,
BE=GH=FG=FE=b,且图中各三
角形均为全等的直角三角形。当且仅当a=b时等号成立*问题四:上式中等号成立的条件:
_____________________________*问题二:上式中等号成立的条件:
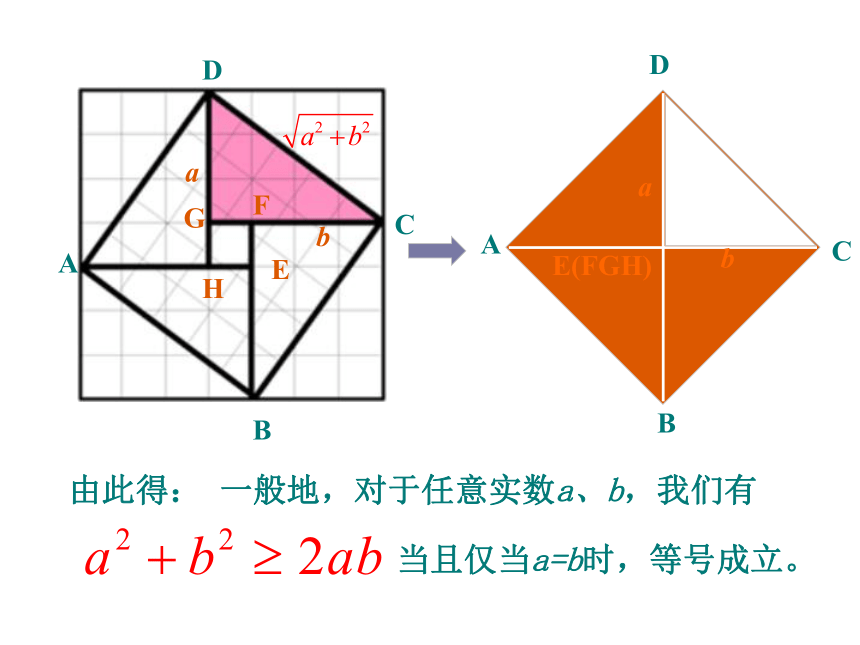
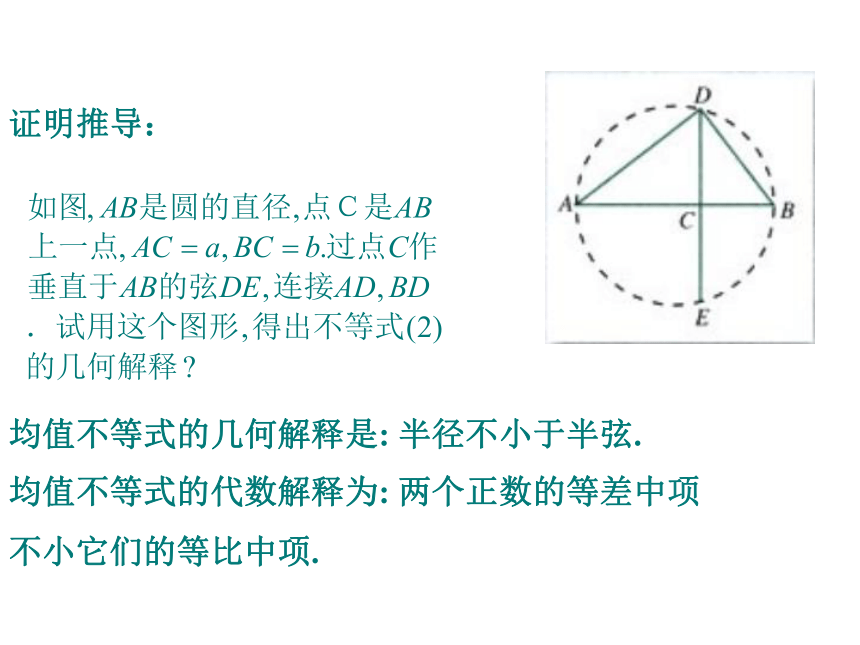
_____________________________得出结论:a2+b2 ≥2ab(a,b∈R)当且仅当a=b时,等号成立。*问题三:当a>0,b>0时,由上式得: 得出结论:当且仅当a=b时,取“=”号证明推导:均值不等式的几何解释是: 半径不小于半弦.均值不等式的代数解释为: 两个正数的等差中项不小它们的等比中项.二、新课讲解其中当且仅当a=b时取等号.二、知识点2:均值不等式的简单应用(当且仅当a=b时,取“=”号)常见
变形例1:已知x>0, y>0, xy=16, 求x+y的最小值,
并说明此时x,y的值.可以应用均值不
等式的先决条件存在最值能够取到最
值的条件例2:已知2x+3y=2(x>0,y>0)求xy 的最大值。如果积xy是定值P,那么x+y≥2 ,
当x=y时,x+y=2 ,即x+y有最小值.如果和x+y是定值S,那么xy≤ ,
当x=y时,xy= ,即xy有最大值.小结1:(当且仅当a=b时,取“=”号)简言之:(积定和最小) 简言之:(和定积最大)三、课堂检测:1、当x>0时, 的最小值为 ,此时x= 。 3、若实数 且 ,则
的最小值是( )
A、10 B、 C、 D、 D212.已知x>0, y>0, xy=24, 求4x+6y的最小值,并说明此时x,y的值.解答过程2.已知x>0, y>0, xy=24, 求4x+6y的最小值,并说明此时x,y的值.返回上页(1)一正:各项均为正数(2)二定:两个正数积为定值,和有最小值.
(积定和最小)
两个正数和为定值,积有最大值.
(和定积最大)(3)三相等:求最值时一定要考虑不等式是否能取“=”,否则会出现错误(取不到等号则说明无最值)提示:构造积为定值,利用基本不等式求最值提示:构造和为定值,利用基本不等式求最值五、课后思考与探究
BE=GH=FG=FE=b,且图中各三
角形均为全等的直角三角形。当且仅当a=b时等号成立*问题四:上式中等号成立的条件:
_____________________________*问题二:上式中等号成立的条件:
_____________________________得出结论:a2+b2 ≥2ab(a,b∈R)当且仅当a=b时,等号成立。*问题三:当a>0,b>0时,由上式得: 得出结论:当且仅当a=b时,取“=”号证明推导:均值不等式的几何解释是: 半径不小于半弦.均值不等式的代数解释为: 两个正数的等差中项不小它们的等比中项.二、新课讲解其中当且仅当a=b时取等号.二、知识点2:均值不等式的简单应用(当且仅当a=b时,取“=”号)常见
变形例1:已知x>0, y>0, xy=16, 求x+y的最小值,
并说明此时x,y的值.可以应用均值不
等式的先决条件存在最值能够取到最
值的条件例2:已知2x+3y=2(x>0,y>0)求xy 的最大值。如果积xy是定值P,那么x+y≥2 ,
当x=y时,x+y=2 ,即x+y有最小值.如果和x+y是定值S,那么xy≤ ,
当x=y时,xy= ,即xy有最大值.小结1:(当且仅当a=b时,取“=”号)简言之:(积定和最小) 简言之:(和定积最大)三、课堂检测:1、当x>0时, 的最小值为 ,此时x= 。 3、若实数 且 ,则
的最小值是( )
A、10 B、 C、 D、 D212.已知x>0, y>0, xy=24, 求4x+6y的最小值,并说明此时x,y的值.解答过程2.已知x>0, y>0, xy=24, 求4x+6y的最小值,并说明此时x,y的值.返回上页(1)一正:各项均为正数(2)二定:两个正数积为定值,和有最小值.
(积定和最小)
两个正数和为定值,积有最大值.
(和定积最大)(3)三相等:求最值时一定要考虑不等式是否能取“=”,否则会出现错误(取不到等号则说明无最值)提示:构造积为定值,利用基本不等式求最值提示:构造和为定值,利用基本不等式求最值五、课后思考与探究
