三角形全等的判定(一)
图片预览



文档简介
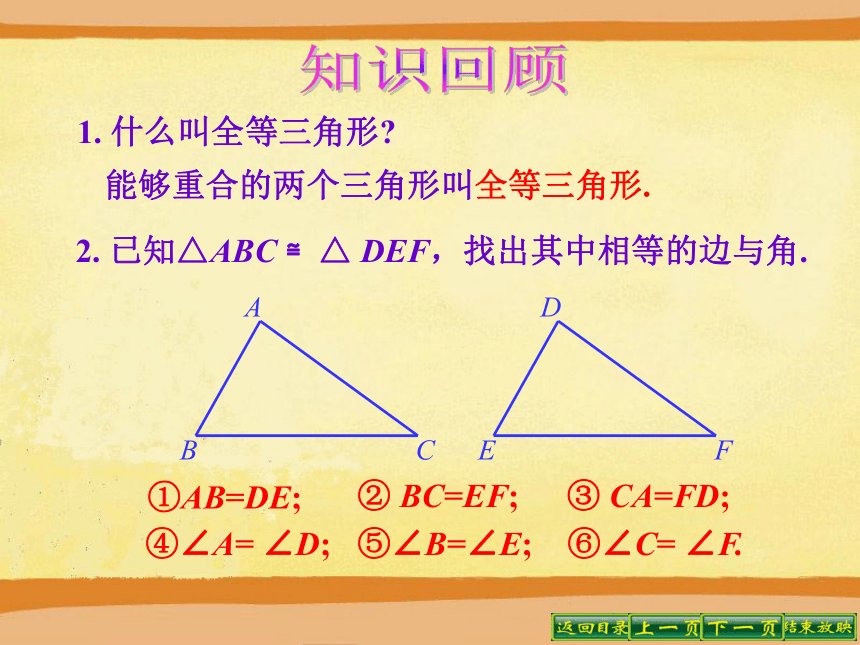
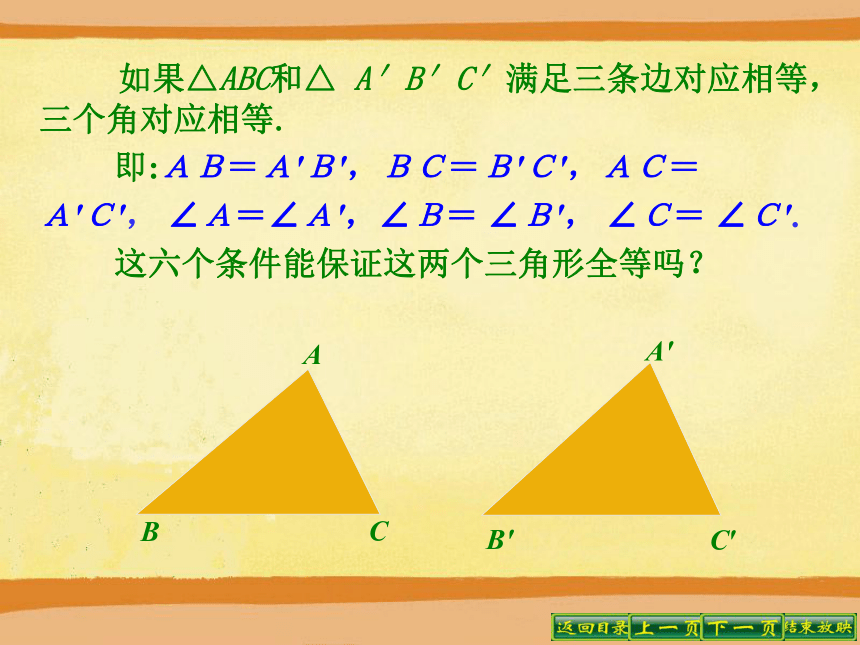
课件21张PPT。单击页面即可演示11.2三角形全等的判定(一) 知识回顾 1. 什么叫全等三角形?能够重合的两个三角形叫全等三角形. 2. 已知△ABC ≌△ DEF,找出其中相等的边与角.①AB=DE;③ CA=FD;② BC=EF; ④∠A= ∠D;⑤∠B=∠E;⑥∠C= ∠F. 如果△ABC和△ A′B′C′满足三条边对应相等,三个角对应相等.
即:AB=A′B′,BC=B′C′,AC=
A′C′, ∠A=∠A′,∠B= ∠B′, ∠C= ∠C′.
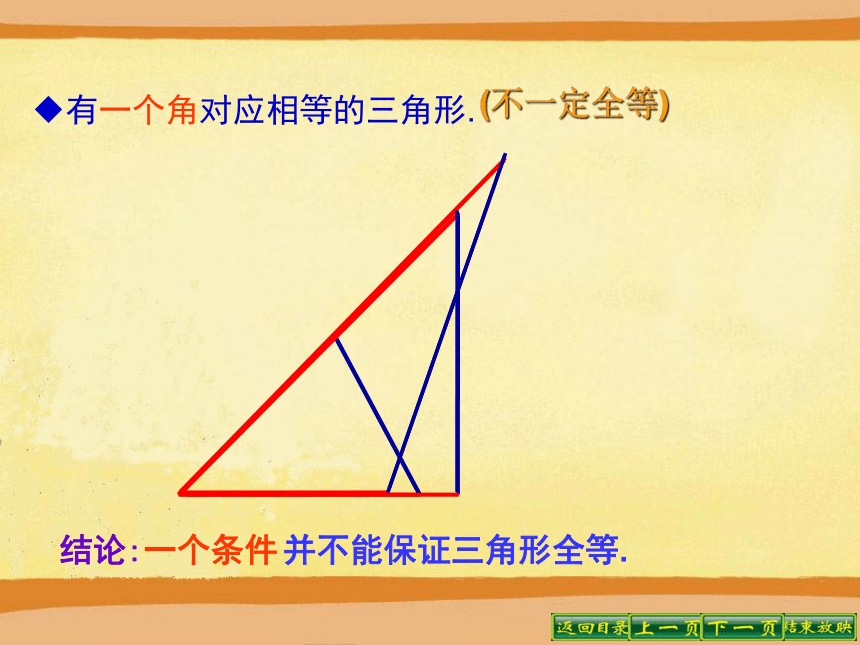
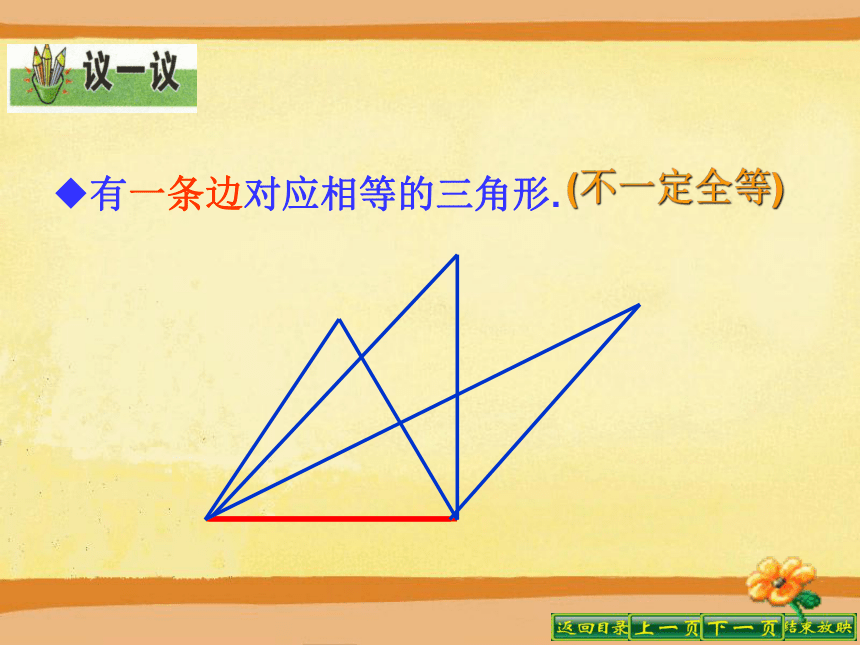
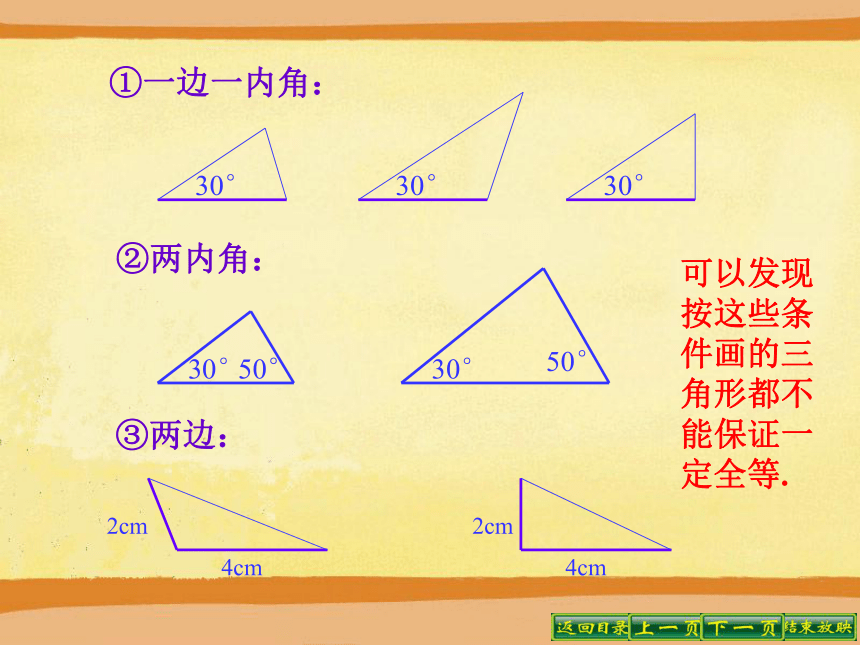
这六个条件能保证这两个三角形全等吗? 先任意画一个△ABC,再画△A′B′C′,使△ABC与△A′B′C′满足上述六个条件中的一个或者两个,这两个三角形一定全等吗?试一试.有一个角对应相等的三角形. 结论:一个条件并不能保证三角形全等.(不一定全等)有一条边对应相等的三角形.(不一定全等) 给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做.
(1)三角形的一个内角为30°,一条边为3cm;
(2)三角形的两个内角分别为30°和50°;
(3)三角形的两条边分别为2cm、4cm.
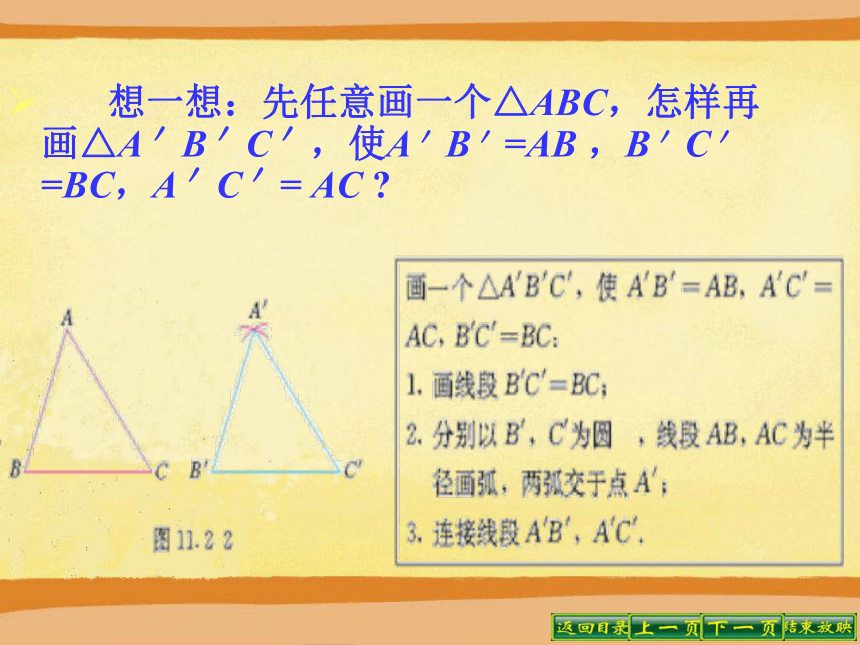
①一边一内角:②两内角:③两边:可以发现按这些条件画的三角形都不能保证一定全等. 想一想:先任意画一个△ABC,怎样再画△A'B'C',使A'B'=AB ,B'C'=BC,A'C'= AC ? 做一做:画△A′B′C′,再把画好的△A′ B′ C′剪下放到△ABC上,看它们重合吗?
说一说:你发现了什么?结论: 全等条件1:三边对应相等的两个三角形全等(简记为“边边边”或“SSS”).ABC用数学符号语言表述:在△ABC和△DEF中,∴ △ABC ≌△ DEF(SSS). AB=DE,
BC=EF,
CA=FD, 木工师傅在做如图所示的门时,通常在门上角处斜钉两根木条,其中的道理是 .三角形具有稳定性 C B 例1 如图, △ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架.
求证: △ABD≌△ACD.
例2 如图,已知AB=CD,BC=DA.
说出下列判断成立的理由:
(1)△ABC≌△CDA;
(2)∠B=∠D. 练习1 如图,已知AB=CD,AD=CB,求证:∠B=∠D.证明:连接AC.AB=CD(已知),AC=AC(公共边),BC=DA(已知),∴ △ ABC≌ △CDA(SSS),∴ ∠B=∠D(全等三角形对应角相等). 在原有条件下,还能推出什么结论? ∠ABC=∠ADC,AB∥CD,AD∥BC. 在△ABC和△CDA中,四边形问题转化为三角形问题解决. 练习2 如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?CBHDA解:有三组. 在△ABH和△ACH中 , ∵AB=AC,BH=CH,AH=AH , ∴△ABH≌△ACH(SSS);∵BD=CD,BH=CH , DH=DH , ∴△DBH≌△DCH(SSS) 在△ABD和△ACD中,
∵AB=AC,BD=CD,AD=AD, ∴△ABD≌△ACD(SSS);在△DBH和△DCH中, (2)如图,D、F是线段BC上的两点,
AB=CE,AF=DE,要△ABF≌△ECD,
还需要条件__________________. B D F C
△ABC ≌ ( ); 解:在△ABC≌△DCB中,理由如下:
AB = CD
AC = BD
=BCBC△DCBBF=DC 或BD=FCABCDSSS 练习3 (1)如图,AB=CD,AC=BD,△ABC和 △DCB是否全等?试说明理由. 小结 为了判断三角形全等,我们可以寻找三组对应相等的边,运用“SSS”的全等条件来判定;
为了推出线段相等,应注意中点、公共边等条件. 谢谢,再见!
即:AB=A′B′,BC=B′C′,AC=
A′C′, ∠A=∠A′,∠B= ∠B′, ∠C= ∠C′.
这六个条件能保证这两个三角形全等吗? 先任意画一个△ABC,再画△A′B′C′,使△ABC与△A′B′C′满足上述六个条件中的一个或者两个,这两个三角形一定全等吗?试一试.有一个角对应相等的三角形. 结论:一个条件并不能保证三角形全等.(不一定全等)有一条边对应相等的三角形.(不一定全等) 给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做.
(1)三角形的一个内角为30°,一条边为3cm;
(2)三角形的两个内角分别为30°和50°;
(3)三角形的两条边分别为2cm、4cm.
①一边一内角:②两内角:③两边:可以发现按这些条件画的三角形都不能保证一定全等. 想一想:先任意画一个△ABC,怎样再画△A'B'C',使A'B'=AB ,B'C'=BC,A'C'= AC ? 做一做:画△A′B′C′,再把画好的△A′ B′ C′剪下放到△ABC上,看它们重合吗?
说一说:你发现了什么?结论: 全等条件1:三边对应相等的两个三角形全等(简记为“边边边”或“SSS”).ABC用数学符号语言表述:在△ABC和△DEF中,∴ △ABC ≌△ DEF(SSS). AB=DE,
BC=EF,
CA=FD, 木工师傅在做如图所示的门时,通常在门上角处斜钉两根木条,其中的道理是 .三角形具有稳定性 C B 例1 如图, △ABC是一个钢架,AB=AC,AD是连接A与BC中点D的支架.
求证: △ABD≌△ACD.
例2 如图,已知AB=CD,BC=DA.
说出下列判断成立的理由:
(1)△ABC≌△CDA;
(2)∠B=∠D. 练习1 如图,已知AB=CD,AD=CB,求证:∠B=∠D.证明:连接AC.AB=CD(已知),AC=AC(公共边),BC=DA(已知),∴ △ ABC≌ △CDA(SSS),∴ ∠B=∠D(全等三角形对应角相等). 在原有条件下,还能推出什么结论? ∠ABC=∠ADC,AB∥CD,AD∥BC. 在△ABC和△CDA中,四边形问题转化为三角形问题解决. 练习2 如图,AB=AC,BD=CD,BH=CH,图中有几组全等的三角形?它们全等的条件是什么?CBHDA解:有三组. 在△ABH和△ACH中 , ∵AB=AC,BH=CH,AH=AH , ∴△ABH≌△ACH(SSS);∵BD=CD,BH=CH , DH=DH , ∴△DBH≌△DCH(SSS) 在△ABD和△ACD中,
∵AB=AC,BD=CD,AD=AD, ∴△ABD≌△ACD(SSS);在△DBH和△DCH中, (2)如图,D、F是线段BC上的两点,
AB=CE,AF=DE,要△ABF≌△ECD,
还需要条件__________________. B D F C
△ABC ≌ ( ); 解:在△ABC≌△DCB中,理由如下:
AB = CD
AC = BD
=BCBC△DCBBF=DC 或BD=FCABCDSSS 练习3 (1)如图,AB=CD,AC=BD,△ABC和 △DCB是否全等?试说明理由. 小结 为了判断三角形全等,我们可以寻找三组对应相等的边,运用“SSS”的全等条件来判定;
为了推出线段相等,应注意中点、公共边等条件. 谢谢,再见!
