角平分线的性质
图片预览

文档简介
课件16张PPT。单击页面即可演示角的平分线的性质11.3问题1:
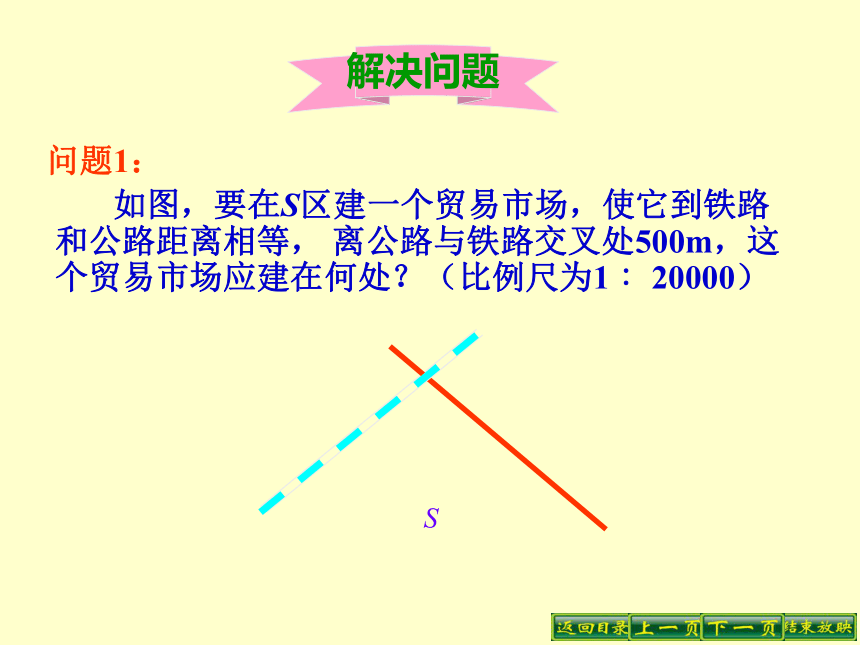
如图,要在S区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处500m,这个贸易市场应建在何处?(比例尺为1 ∶20000)
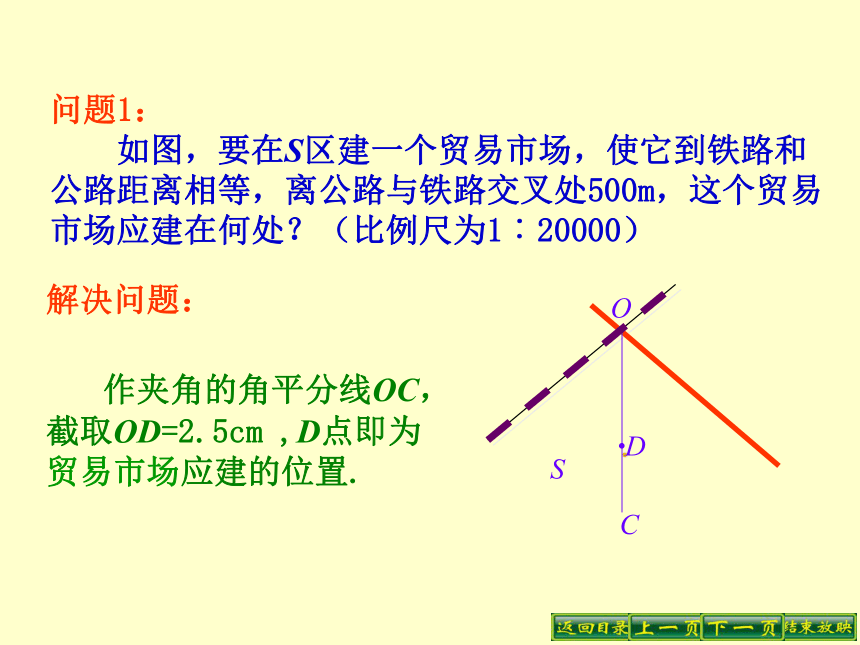
解决问题解决问题: 作夹角的角平分线OC,截取OD=2.5cm ,D点即为 贸易市场应建的位置.问题1:
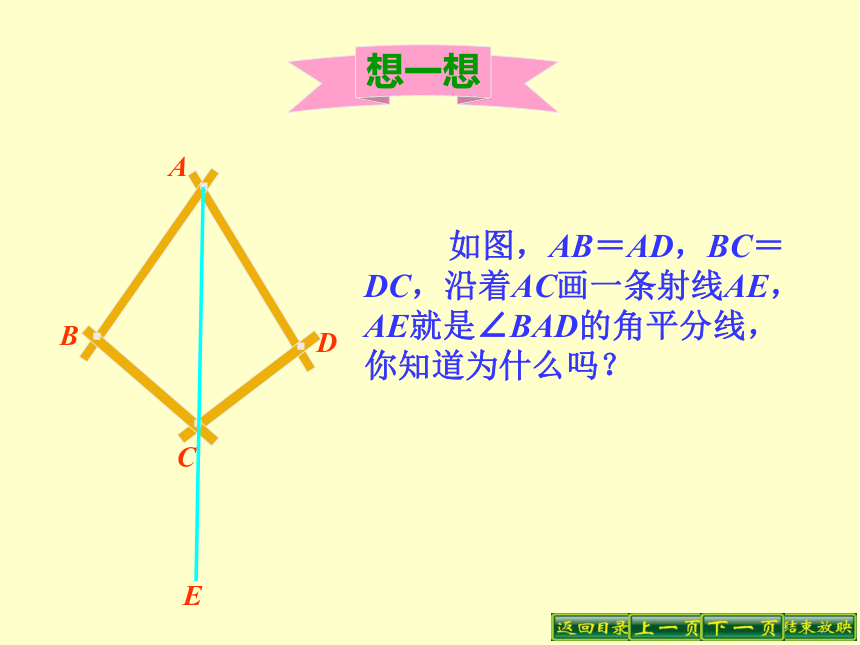
如图,要在S区建一个贸易市场,使它到铁路和公路距离相等,离公路与铁路交叉处500m,这个贸易市场应建在何处?(比例尺为1︰20000)O. 如图,AB=AD,BC=DC,沿着AC画一条射线AE,AE就是∠BAD的角平分线,你知道为什么吗?想一想 证明:在△ADC和△ABC 中,
AB=AD(已知),
AC=AC(公共边相等),
DC=BC(已知),
∴ △ADC≌△ABC (SSS).
∴∠DAC=∠BAC(全等三角形对应角相等),
∴ AE平分∠BAD(角平分线定义).
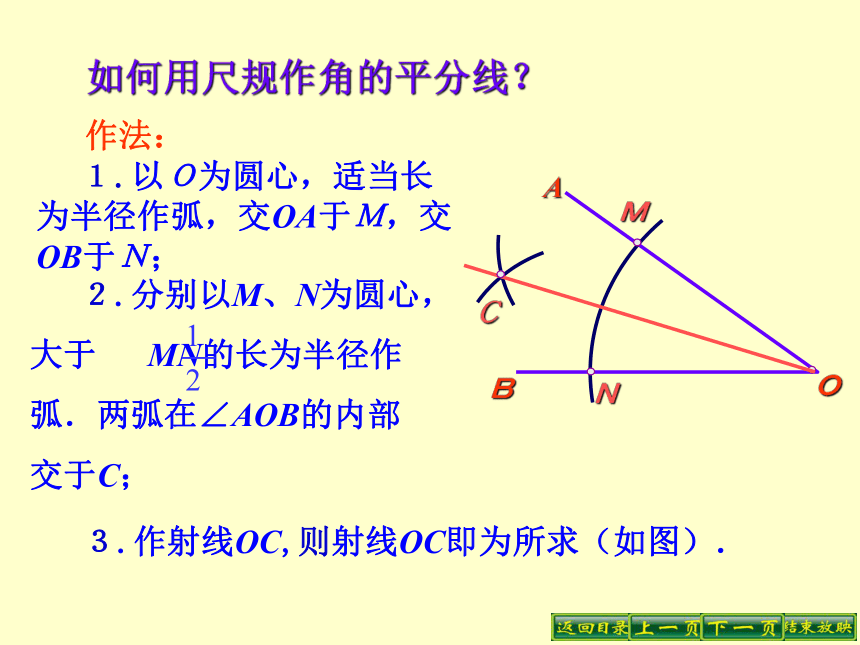
2.分别以M、N为圆心,大于 MN的长为半径作弧.两弧在∠AOB的内部交于C; 如何用尺规作角的平分线?ABOMC 作法: 1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N; 3.作射线OC,则射线OC即为所求(如图). 观察折纸思考问题:
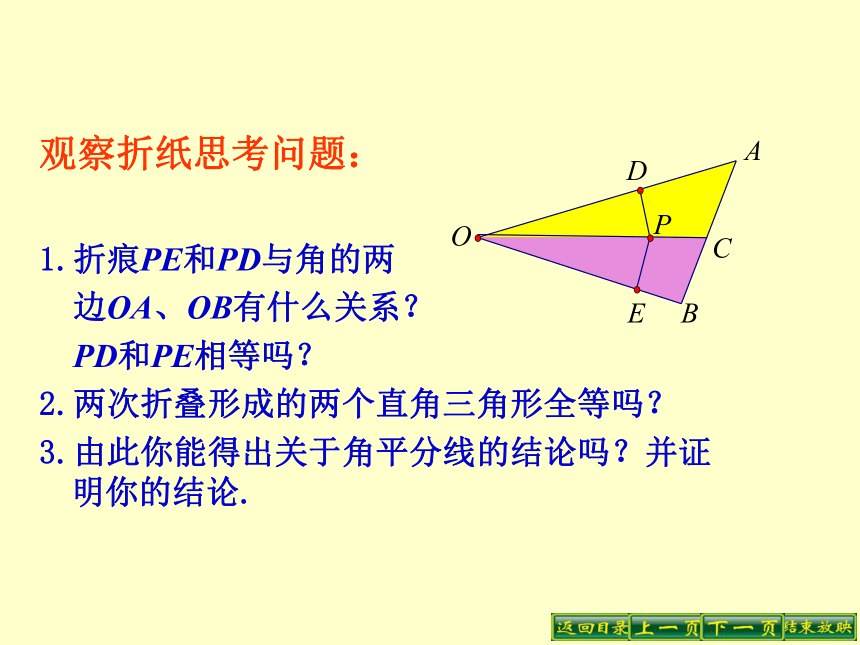
1.折痕PE和PD与角的两
边OA、OB有什么关系?
PD和PE相等吗?
2.两次折叠形成的两个直角三角形全等吗?
3.由此你能得出关于角平分线的结论吗?并证 明你的结论.
已知:如图, OC平分∠AOB, P是OC上一点, PD⊥OA,PE⊥OB .
求证:PD=PE.
证明: ∵OC平分∠AOB, P是OC上一
点(已知),
∴∠DOP=∠EOP(角平分线定义),
∵PD⊥OA,PE⊥OB (已知),
∴∠ODP=∠OEP=90°(垂直的定义).角平分线性质:
角平分线上的点到这个角的两边距离相等. 几何语言:
∵OC是∠AOB的平分线,PD⊥OA,PE⊥OB,
∴PD=PE(角平分线上的点到这个角两边的距 离相等). 在△OPD和△OPE中,
∠DOP=∠BOP(已证),
∠ODP=∠OEP(已证),
OP=OP (已知),
∴△OPD ≌△OPE(AAS),
∴PD=PE(全等三角形对应边相等). 反过来,到一个角的两边的距离相等的点是否一定在这个角的平分线上呢? 已知:如图,QD⊥OA、QE⊥OB,
点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.思 考 证明:∵ QD⊥OA,QE⊥OB(已知),
∴ ∠QDO=∠QEO=90°(垂直的定义), 在Rt△QDO和Rt△QEO中,
QO=QO(公共边), QD=QE(已知),
∴ Rt△QDO≌Rt△QEO(HL).
∴ ∠QOD=∠QOE,
∴ 点Q在∠AOB的平分线上.已知:如图,QD⊥OA,QE⊥OB,
点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.到角的两边的距离相等的点在角的平分线上.∵ QD⊥OA,QE⊥OB,QD=QE,
∴ 点Q在∠AOB的平分线上.用数学语言表示为:角的平分线上的点到角的两边的距离相等.∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上,
∴ QD=QE.用数学语言表示为:例1 已知:如图,△ABC的角平分线BM、CN相交于点P.求证:点P到三边AB、BC、CA的距离相等.FABCPMN 练习:如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,求证:点F在∠DAE的平分线上.
证明:过点F作FG⊥AE于G,FM⊥BC于M ,,FH⊥AD于H.GHM∵点F在∠BCE的平分线上, FG⊥AE,FM⊥BC.∴FG=FM.又∵点F在∠CBD的平分线上, FH⊥AD,FM⊥BC.∴FM=FH,∴FG=FH,∴点F在∠DAE的平分线上. 1.角平分线的性质定理:
在角平分线上的点到角的两边的距离相等.
2.角平分线的判定定理:
到一个角的两边的距离相等的点在这个角的平分线上.
3.角平分线的性质定理和角平分线的判定定理是证明
角相等、线段相等的新途径. 本节课学习了哪些知识?有哪些运用?你学会了吗?做了吗?用了吗?小 结谢谢,再见!
如图,要在S区建一个贸易市场,使它到铁路和公路距离相等, 离公路与铁路交叉处500m,这个贸易市场应建在何处?(比例尺为1 ∶20000)
解决问题解决问题: 作夹角的角平分线OC,截取OD=2.5cm ,D点即为 贸易市场应建的位置.问题1:
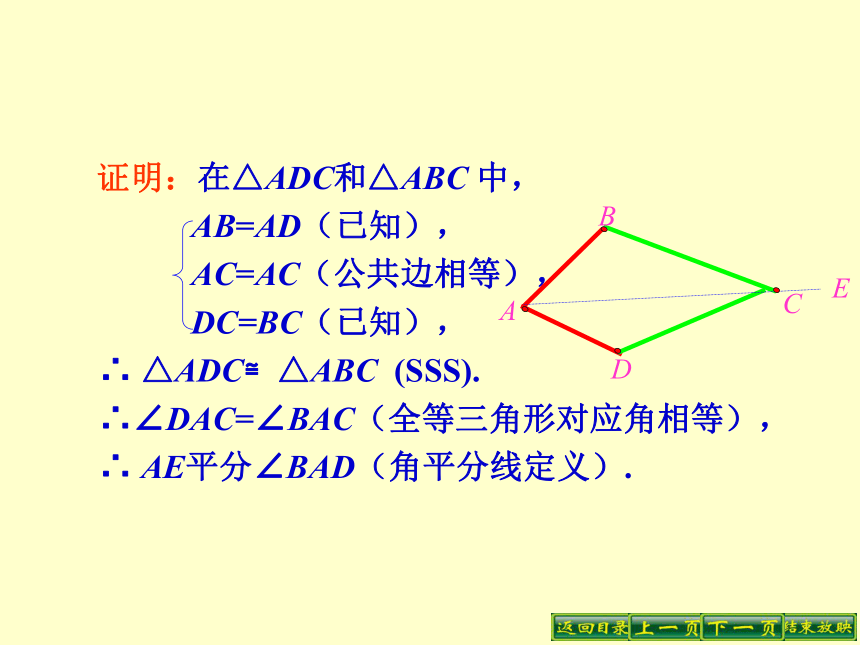
如图,要在S区建一个贸易市场,使它到铁路和公路距离相等,离公路与铁路交叉处500m,这个贸易市场应建在何处?(比例尺为1︰20000)O. 如图,AB=AD,BC=DC,沿着AC画一条射线AE,AE就是∠BAD的角平分线,你知道为什么吗?想一想 证明:在△ADC和△ABC 中,
AB=AD(已知),
AC=AC(公共边相等),
DC=BC(已知),
∴ △ADC≌△ABC (SSS).
∴∠DAC=∠BAC(全等三角形对应角相等),
∴ AE平分∠BAD(角平分线定义).
2.分别以M、N为圆心,大于 MN的长为半径作弧.两弧在∠AOB的内部交于C; 如何用尺规作角的平分线?ABOMC 作法: 1.以O为圆心,适当长为半径作弧,交OA于M,交OB于N; 3.作射线OC,则射线OC即为所求(如图). 观察折纸思考问题:
1.折痕PE和PD与角的两
边OA、OB有什么关系?
PD和PE相等吗?
2.两次折叠形成的两个直角三角形全等吗?
3.由此你能得出关于角平分线的结论吗?并证 明你的结论.
已知:如图, OC平分∠AOB, P是OC上一点, PD⊥OA,PE⊥OB .
求证:PD=PE.
证明: ∵OC平分∠AOB, P是OC上一
点(已知),
∴∠DOP=∠EOP(角平分线定义),
∵PD⊥OA,PE⊥OB (已知),
∴∠ODP=∠OEP=90°(垂直的定义).角平分线性质:
角平分线上的点到这个角的两边距离相等. 几何语言:
∵OC是∠AOB的平分线,PD⊥OA,PE⊥OB,
∴PD=PE(角平分线上的点到这个角两边的距 离相等). 在△OPD和△OPE中,
∠DOP=∠BOP(已证),
∠ODP=∠OEP(已证),
OP=OP (已知),
∴△OPD ≌△OPE(AAS),
∴PD=PE(全等三角形对应边相等). 反过来,到一个角的两边的距离相等的点是否一定在这个角的平分线上呢? 已知:如图,QD⊥OA、QE⊥OB,
点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.思 考 证明:∵ QD⊥OA,QE⊥OB(已知),
∴ ∠QDO=∠QEO=90°(垂直的定义), 在Rt△QDO和Rt△QEO中,
QO=QO(公共边), QD=QE(已知),
∴ Rt△QDO≌Rt△QEO(HL).
∴ ∠QOD=∠QOE,
∴ 点Q在∠AOB的平分线上.已知:如图,QD⊥OA,QE⊥OB,
点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.到角的两边的距离相等的点在角的平分线上.∵ QD⊥OA,QE⊥OB,QD=QE,
∴ 点Q在∠AOB的平分线上.用数学语言表示为:角的平分线上的点到角的两边的距离相等.∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上,
∴ QD=QE.用数学语言表示为:例1 已知:如图,△ABC的角平分线BM、CN相交于点P.求证:点P到三边AB、BC、CA的距离相等.FABCPMN 练习:如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,求证:点F在∠DAE的平分线上.
证明:过点F作FG⊥AE于G,FM⊥BC于M ,,FH⊥AD于H.GHM∵点F在∠BCE的平分线上, FG⊥AE,FM⊥BC.∴FG=FM.又∵点F在∠CBD的平分线上, FH⊥AD,FM⊥BC.∴FM=FH,∴FG=FH,∴点F在∠DAE的平分线上. 1.角平分线的性质定理:
在角平分线上的点到角的两边的距离相等.
2.角平分线的判定定理:
到一个角的两边的距离相等的点在这个角的平分线上.
3.角平分线的性质定理和角平分线的判定定理是证明
角相等、线段相等的新途径. 本节课学习了哪些知识?有哪些运用?你学会了吗?做了吗?用了吗?小 结谢谢,再见!
