(新人教a版-选修2-3)数学:2.2.3《二项分布及其应用--独立重复试验》课件
文档属性
| 名称 | (新人教a版-选修2-3)数学:2.2.3《二项分布及其应用--独立重复试验》课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 131.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-19 00:00:00 | ||
图片预览








文档简介
课件26张PPT。2.2.3《二项分布及其应用
--独立重复试验》教学目标 知识与技能:理解n次独立重复试验的模型及二项分布,并能解答一些简单的实际问题。
过程与方法:能进行一些与n次独立重复试验的模型及二项分布有关的概率的计算。
情感、态度与价值观:承前启后,感悟数学与生活的和谐之美 ,体现数学的文化功能与人文价值。
教学重点:理解n次独立重复试验的模型及二项分布,并能解答一些简单的实际问题
教学难点:能进行一些与n次独立重复试验的模型及二项分布有关的概率的计算
授课类型:新授课 课时安排:1课时 教 具:多媒体、实物投影仪 独立重复试验的定义:
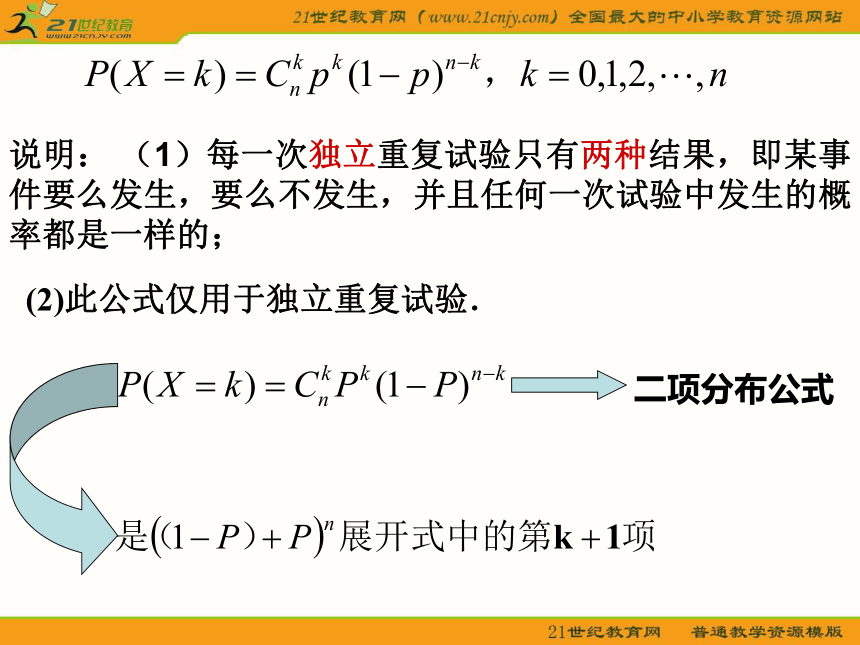
一般地,在相同条件下重复做的n次试验称为n次独立重复实验在n次独立重复试验中,“在相同的条件下”等价于各次试验的结果不会受其他试验的影响,即掷一枚图钉,设针尖向上的概率为p,则针尖向下的概率是q=1-p,连续掷一枚图钉3次,仅出现1次针尖向上的概率是多少?类似可以得到:可以发现 一般地,在n次独立重复试验中,设事件A发生的次数为X,在每次试验中事件A发生的概率是P,那么在n次独立重复试验中,这个事件恰好发生k次的概率此时称随机变量X服从二项分布,记作X~B(n,p),并称p为成功概率。说明: (1)每一次独立重复试验只有两种结果,即某事件要么发生,要么不发生,并且任何一次试验中发生的概率都是一样的;(2)此公式仅用于独立重复试验.二项分布公式例1 设一射手平均每射击10次中靶4次,求在五次射击中①击中一次,②第二次击中,③击中两次,④第二、三两次击中,⑤至少击中一次的概率.由题设,此射手射击1次,中靶的概率为0.4.① n=5,k=1,应用公式得② 事件“第二次击中”表示第一、三、四、五次击中或击不中都可,它不同于“击中一次”,也不同于“第二次击中,其他各次都不中”,不能用公式.它的概率就是0.4.③n=5,k=2,④“第二、三两次击中”表示第一次、第四次及第五次可中可不中,所以概率为0.4×0.4=0.16.⑤设“至少击中一次”为事件B,则B包括“击中一次”,“击中两次”,“击中三次”,“击中四次”,“击中五次”,所以概率为P(B)=P(1)+P(2)+P(3)+P(4)+P(5)
=0.2592+0.3456+0.2304+0.0768+0.01024
=0.92224.1-P(0)例1 设一射手平均每射击10次中靶4次,求在五次射击中①击中一次,②第二次击中,③击中两次,④第二、三两次击中,⑤至少击中一次的概率.例4 某射手每次射击击中目标的概率是0.8,求这名射手在10次射击中,
(1)恰有8次击中目标的概率;
(2)至少有8次击中目标的概率。解:设X为击中目标的次数,则X~B(10,0.8)(1)在10次射击中,恰有8次击中目标的概率为(2)在10次射击中,至少有8次击中目标的概率为例1.设3次独立重复试验中,事件A发生的概率相等,若已知A至少发生一次的概率等于19/27,求事件A在一次试验中发生的概率。1.有10门炮同时各向目标各发一枚炮弹,如果每门炮的命中率都是0.1,则目标被击中的概率约是( )
A 0.55 B 0.45 C 0.75 D 0.65 D 练习 2.一射手对同一目标独立地进行4次射击,已知至少命中一次的概率为 ,则此射手射击一次的
命中率是( )
A B C D B3.甲、乙两队参加乒乓球团体比赛,甲队与乙队实力之比为3:2,若比赛时均能正常发挥技术水平,则在5局3胜制中,打完4局才能取胜的概率为( )
A B
C D A 4.一批产品共有100个,次品率为 3% ,从中有放回抽取3个恰有1个次品的概率是( )
A
B
C D A无放回抽取例2.甲、乙两个篮球运动员投篮命中率为0.7及0.6,若每人各投3次,试求甲至少胜乙2个进球的概率 B队队员胜的概率
例4.有10道单项选择题,每题有4个选支,某人随机选定每题中其中一个答案,求答对多少题的概率最大?并求出此种情况下概率的大小.例2.有译电员若干员,每人独立破译密码的概率均为 ,若要达到译出密码的概率为0.99,至少要配备多少人?
(lg2=0.3010,lg3=0.4771) 袋中有12个球,其中白球4个,甲、乙、丙三人接连从袋中取球,甲先取然后乙、丙,再又是甲,如此继续下去,规定先取出一个白球者获胜.分别求满足下列条件的甲、乙、丙的获胜率:
(1)抽后放回;
(2)抽后不放回.( )再见
过程与方法:能进行一些与n次独立重复试验的模型及二项分布有关的概率的计算。
情感、态度与价值观:承前启后,感悟数学与生活的和谐之美 ,体现数学的文化功能与人文价值。
教学重点:理解n次独立重复试验的模型及二项分布,并能解答一些简单的实际问题
教学难点:能进行一些与n次独立重复试验的模型及二项分布有关的概率的计算
授课类型:新授课 课时安排:1课时 教 具:多媒体、实物投影仪 独立重复试验的定义:
一般地,在相同条件下重复做的n次试验称为n次独立重复实验在n次独立重复试验中,“在相同的条件下”等价于各次试验的结果不会受其他试验的影响,即掷一枚图钉,设针尖向上的概率为p,则针尖向下的概率是q=1-p,连续掷一枚图钉3次,仅出现1次针尖向上的概率是多少?类似可以得到:可以发现 一般地,在n次独立重复试验中,设事件A发生的次数为X,在每次试验中事件A发生的概率是P,那么在n次独立重复试验中,这个事件恰好发生k次的概率此时称随机变量X服从二项分布,记作X~B(n,p),并称p为成功概率。说明: (1)每一次独立重复试验只有两种结果,即某事件要么发生,要么不发生,并且任何一次试验中发生的概率都是一样的;(2)此公式仅用于独立重复试验.二项分布公式例1 设一射手平均每射击10次中靶4次,求在五次射击中①击中一次,②第二次击中,③击中两次,④第二、三两次击中,⑤至少击中一次的概率.由题设,此射手射击1次,中靶的概率为0.4.① n=5,k=1,应用公式得② 事件“第二次击中”表示第一、三、四、五次击中或击不中都可,它不同于“击中一次”,也不同于“第二次击中,其他各次都不中”,不能用公式.它的概率就是0.4.③n=5,k=2,④“第二、三两次击中”表示第一次、第四次及第五次可中可不中,所以概率为0.4×0.4=0.16.⑤设“至少击中一次”为事件B,则B包括“击中一次”,“击中两次”,“击中三次”,“击中四次”,“击中五次”,所以概率为P(B)=P(1)+P(2)+P(3)+P(4)+P(5)
=0.2592+0.3456+0.2304+0.0768+0.01024
=0.92224.1-P(0)例1 设一射手平均每射击10次中靶4次,求在五次射击中①击中一次,②第二次击中,③击中两次,④第二、三两次击中,⑤至少击中一次的概率.例4 某射手每次射击击中目标的概率是0.8,求这名射手在10次射击中,
(1)恰有8次击中目标的概率;
(2)至少有8次击中目标的概率。解:设X为击中目标的次数,则X~B(10,0.8)(1)在10次射击中,恰有8次击中目标的概率为(2)在10次射击中,至少有8次击中目标的概率为例1.设3次独立重复试验中,事件A发生的概率相等,若已知A至少发生一次的概率等于19/27,求事件A在一次试验中发生的概率。1.有10门炮同时各向目标各发一枚炮弹,如果每门炮的命中率都是0.1,则目标被击中的概率约是( )
A 0.55 B 0.45 C 0.75 D 0.65 D 练习 2.一射手对同一目标独立地进行4次射击,已知至少命中一次的概率为 ,则此射手射击一次的
命中率是( )
A B C D B3.甲、乙两队参加乒乓球团体比赛,甲队与乙队实力之比为3:2,若比赛时均能正常发挥技术水平,则在5局3胜制中,打完4局才能取胜的概率为( )
A B
C D A 4.一批产品共有100个,次品率为 3% ,从中有放回抽取3个恰有1个次品的概率是( )
A
B
C D A无放回抽取例2.甲、乙两个篮球运动员投篮命中率为0.7及0.6,若每人各投3次,试求甲至少胜乙2个进球的概率 B队队员胜的概率
例4.有10道单项选择题,每题有4个选支,某人随机选定每题中其中一个答案,求答对多少题的概率最大?并求出此种情况下概率的大小.例2.有译电员若干员,每人独立破译密码的概率均为 ,若要达到译出密码的概率为0.99,至少要配备多少人?
(lg2=0.3010,lg3=0.4771) 袋中有12个球,其中白球4个,甲、乙、丙三人接连从袋中取球,甲先取然后乙、丙,再又是甲,如此继续下去,规定先取出一个白球者获胜.分别求满足下列条件的甲、乙、丙的获胜率:
(1)抽后放回;
(2)抽后不放回.( )再见
