圆的对称性(一)
图片预览





文档简介
课件12张PPT。第三章 圆 第二节 圆的对称性(一)
平和广兆中学2019-3-10问题:
前面我们已探讨过轴对称图形,哪位同学能叙述一下轴对称图形的定义?我们是用什么方法研究轴对称图形的? I.创设问题情境,引入新课 2019-3-10Ⅱ.讲授新课 圆是轴对称图形吗?
如果是,它的对称轴是什么?
你能找到多少条对称轴?
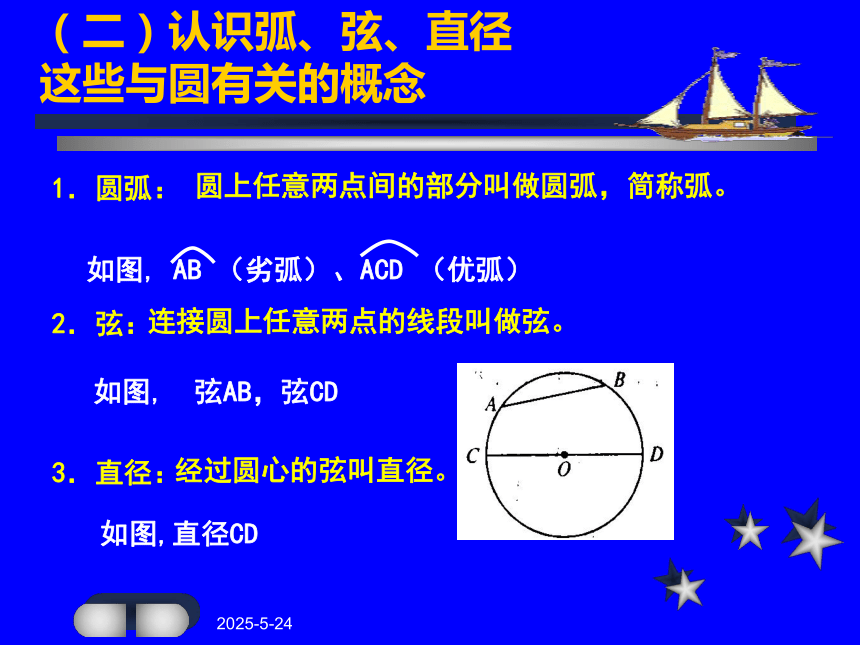
讨论:你是用什么方法解决上述问题的? 归纳:圆是轴对称图形,其对称轴是任意一条过圆心的直线(一)想一想2019-3-10(二)认识弧、弦、直径这些与圆有关的概念 2.弦:3.直径:1.圆弧:如图, AB (劣弧)、ACD (优弧)如图, 弦AB,弦CD如图,直径CD圆上任意两点间的部分叫做圆弧,简称弧。连接圆上任意两点的线段叫做弦。经过圆心的弦叫直径。2019-3-10(三)探索垂径定理
1.在一张纸上任意画一个⊙O,沿圆周将圆剪下,把这个圆对折,使圆的两半部分重合.
2.得到一条折痕CD.
3.在⊙O上任取一点A,过点A作CD折痕 的垂线,得到新的折痕,其中,点M是两条折痕的交点,即垂足.
4.将纸打开,新的折痕与圆交于另一点B,如图.问题:(1)右图是轴对称图形吗?
如果是,其对称轴是什么?
(2)你能发现图中有哪些等量关系?
说一说你的理由。做一做:按下面的步骤做一做2019-3-10推理格式:如图所示
∵CD⊥AB,CD为⊙O的直径
∴AM=BM,AD=BD,AC=BC.总结得出垂径定理:
垂直于弦的直径平分这条弦,并且平分弦所对的弧。⌒⌒⌒⌒2019-3-10
[例]如右图所示,一条公路的转弯处是
一段圆弧(即图中CD,点O是CD的圆心),
其中CD=600m,E为CD上一点,且
OE⊥CD,垂足为F,EF=90 m.求这段弯
路的半径.[分析]要求弯路的半径,连接OC,只要求出OC的长便可以了.
因为已知OE⊥CD,所以CF=CD=300 cm,OF=OE-EF,
此时得到了一个Rt△CFO,利用勾股定理便可列出方程.(四)讲例⌒⌒⌒2019-3-10
练一练:完成课本随堂练习第1题.
2019-3-10(五)探索垂径定理的逆定理1.想一想:如下图示,AB是⊙O的弦(不是直径),作一条平分AB的直径CD,交AB于点M.
同学们利用圆纸片动手做一做,然后回答:(1)此图是轴对称图形吗?如果是,其对称轴是什么?(2)你能发现图中有哪些等量关系?说一说你的理由。
2019-3-10练一练:完成课本随堂练习第2题.2019-3-10Ⅲ.课时小结 1.本节课我们探索了圆的对称性.
2.利用圆的轴对称性研究了垂径定理及其逆定理.
3.垂径定理和勾股定理相结合,构造直角三角形,可解决弦长、半径、弦心距等计算问题.2019-3-10Ⅳ .课后作业
(一)课本习题3.2,1、2.试一试1.
(二) 预习课本:P94~97内容
BYE-BYE!2019-3-10
前面我们已探讨过轴对称图形,哪位同学能叙述一下轴对称图形的定义?我们是用什么方法研究轴对称图形的? I.创设问题情境,引入新课 2019-3-10Ⅱ.讲授新课 圆是轴对称图形吗?
如果是,它的对称轴是什么?
你能找到多少条对称轴?
讨论:你是用什么方法解决上述问题的? 归纳:圆是轴对称图形,其对称轴是任意一条过圆心的直线(一)想一想2019-3-10(二)认识弧、弦、直径这些与圆有关的概念 2.弦:3.直径:1.圆弧:如图, AB (劣弧)、ACD (优弧)如图, 弦AB,弦CD如图,直径CD圆上任意两点间的部分叫做圆弧,简称弧。连接圆上任意两点的线段叫做弦。经过圆心的弦叫直径。2019-3-10(三)探索垂径定理
1.在一张纸上任意画一个⊙O,沿圆周将圆剪下,把这个圆对折,使圆的两半部分重合.
2.得到一条折痕CD.
3.在⊙O上任取一点A,过点A作CD折痕 的垂线,得到新的折痕,其中,点M是两条折痕的交点,即垂足.
4.将纸打开,新的折痕与圆交于另一点B,如图.问题:(1)右图是轴对称图形吗?
如果是,其对称轴是什么?
(2)你能发现图中有哪些等量关系?
说一说你的理由。做一做:按下面的步骤做一做2019-3-10推理格式:如图所示
∵CD⊥AB,CD为⊙O的直径
∴AM=BM,AD=BD,AC=BC.总结得出垂径定理:
垂直于弦的直径平分这条弦,并且平分弦所对的弧。⌒⌒⌒⌒2019-3-10
[例]如右图所示,一条公路的转弯处是
一段圆弧(即图中CD,点O是CD的圆心),
其中CD=600m,E为CD上一点,且
OE⊥CD,垂足为F,EF=90 m.求这段弯
路的半径.[分析]要求弯路的半径,连接OC,只要求出OC的长便可以了.
因为已知OE⊥CD,所以CF=CD=300 cm,OF=OE-EF,
此时得到了一个Rt△CFO,利用勾股定理便可列出方程.(四)讲例⌒⌒⌒2019-3-10
练一练:完成课本随堂练习第1题.
2019-3-10(五)探索垂径定理的逆定理1.想一想:如下图示,AB是⊙O的弦(不是直径),作一条平分AB的直径CD,交AB于点M.
同学们利用圆纸片动手做一做,然后回答:(1)此图是轴对称图形吗?如果是,其对称轴是什么?(2)你能发现图中有哪些等量关系?说一说你的理由。
2019-3-10练一练:完成课本随堂练习第2题.2019-3-10Ⅲ.课时小结 1.本节课我们探索了圆的对称性.
2.利用圆的轴对称性研究了垂径定理及其逆定理.
3.垂径定理和勾股定理相结合,构造直角三角形,可解决弦长、半径、弦心距等计算问题.2019-3-10Ⅳ .课后作业
(一)课本习题3.2,1、2.试一试1.
(二) 预习课本:P94~97内容
BYE-BYE!2019-3-10
