等腰三角形的性质
图片预览


文档简介
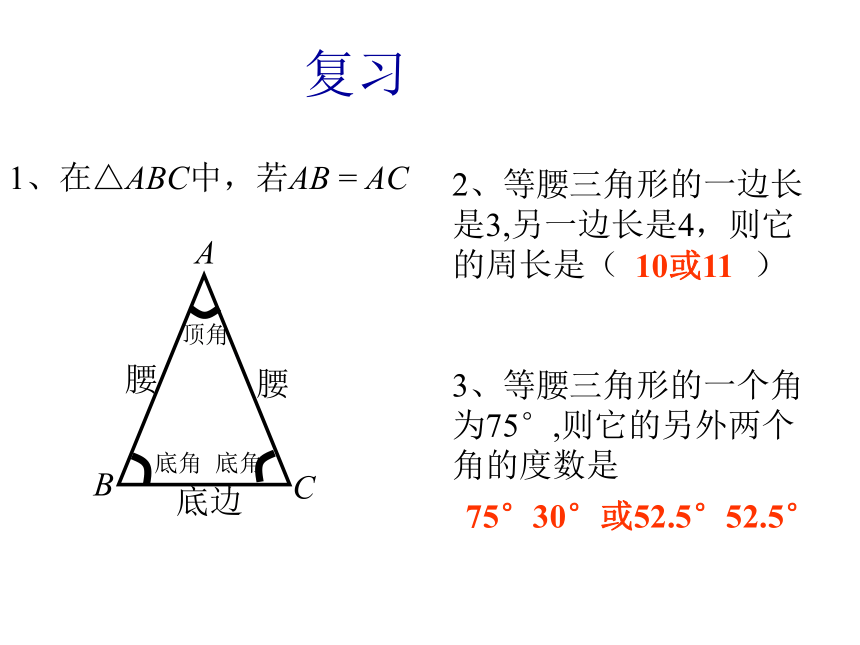
课件11张PPT。复习1、在△ABC中,若AB = AC底边顶角2、等腰三角形的一边长是3,另一边长是4,则它的周长是( )
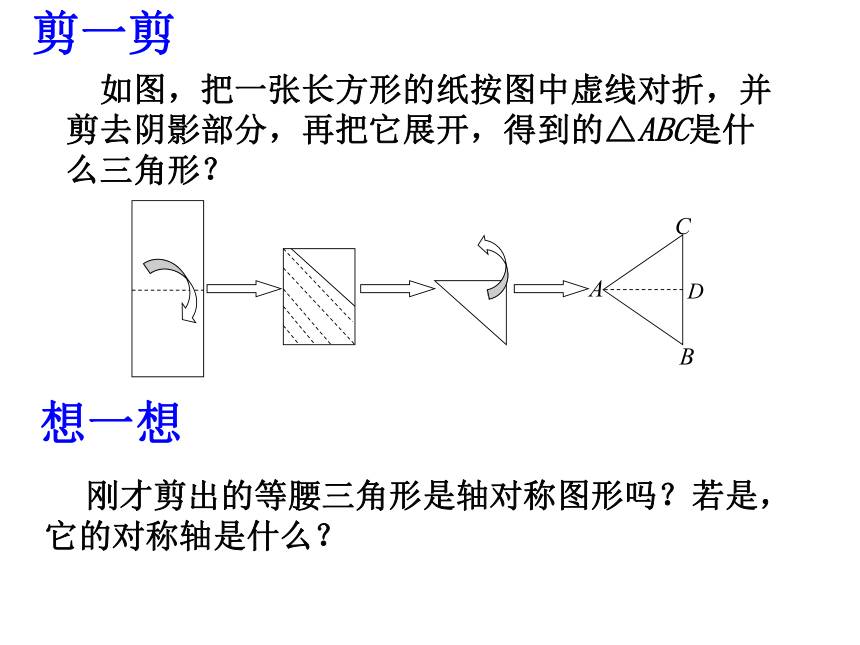
3、等腰三角形的一个角为75°,则它的另外两个角的度数是10或1175°30°或52.5°52.5°剪一剪 如图,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC是什么三角形?
想一想
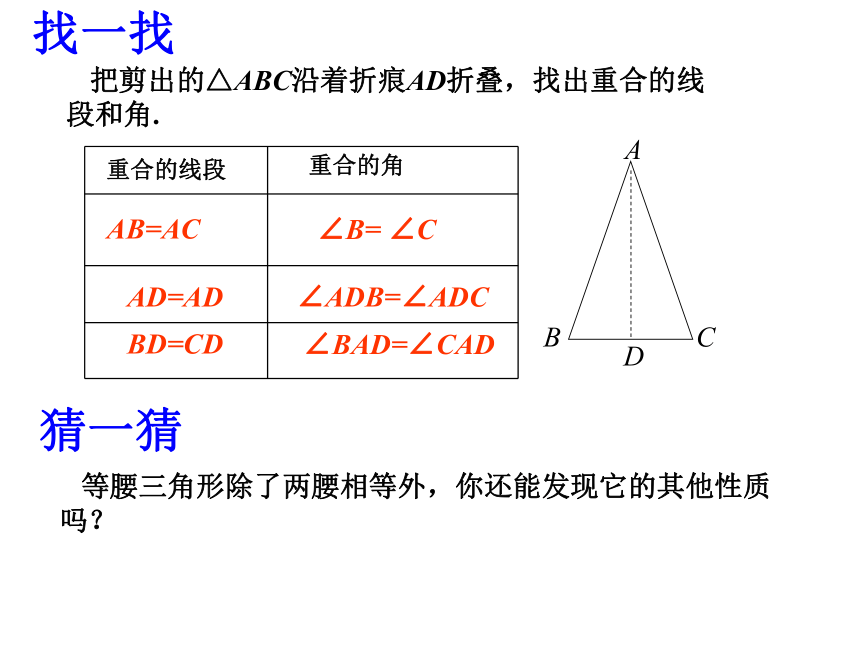
刚才剪出的等腰三角形是轴对称图形吗?若是,它的对称轴是什么? 把剪出的△ABC沿着折痕AD折叠,找出重合的线段和角.找一找 猜一猜 等腰三角形除了两腰相等外,你还能发现它的其他性质吗?AB=ACAD=ADBD=CD∠B= ∠C∠ADB=∠ADC∠BAD=∠CAD性质1、等腰三角形的两个底角相等求证:∠B =∠C 已知: △ABC 中,AB=AC证明:作底边BC边上的中线AD
在△ABD与△ACD中:
AB=AC(已知)
BD=DC(已作)
AD=AD(公共边)
∴△ABD≌△ACD(SSS)
∴∠B=∠C(全等三角形对应角相等)证明:作顶角∠BAC的平分线AD
∵AD平分∠BAC
∴∠1=∠2
在△ABD与△ACD中
AB=AC(已知)
∠1=∠2(已证)
AD=AD(公共边)
∴ △ABD ≌ △ACD(SAS)
∴ ∠B=∠C
证明:作底边BC的高AD。
∵AD⊥BC
∴ ∠ADB =∠ADC=90°
在Rt△ABD与Rt△ACD中
AB=AC(已知)
AD=AD(公共边)
∴ Rt △ABD ≌ Rt △ACD
∴ ∠B=∠C议一议:说说为什么在添加辅助线时,作顶角平分线,底边中线,底边高都能使分成的两个三角形全等?性质1、等腰三角形的两个底角相等由△ABD ≌ △ACD,你还能得出什么结论?性质2 等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合(简称三线合一) 已知:△ABC中,AB=AC、BD平分∠ABC。
能否推出BD⊥AC、DA=DC吗?典型例题 如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD.
求△ABC各角的度数.提示:1、图中有几个等腰三角形?
2、可以得到哪些角相等?
3、若设∠A= x,你还能能用 x表示哪些角?解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠3, ∠A =∠1(等边对等角).
设∠A = x,则∠3= ∠A + ∠1=2x
∴∠ABC=∠C=∠3=2x
∵ ∠A+ ∠ABC+∠C = 180°
∴ x+2x+2x= 180°
解得:x=36°
∴ ∠A =36° ∴∠ABC=∠C=72° 已知:△ABC中,AB=AC,D是BC边上的中点,DF⊥AC于F DE ⊥ AB 于E .
求证:DE=DF. 证明: ∵DE⊥AB,DF⊥AC(已知)
∴∠BED=∠CFD
又∵D是BC中点(已知)
∴BD=DC
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
在△DBE与△DCF中
∠DEB=∠DFC(已证)
∠B=∠C(已证)
BD=DC(已证)
∴ △BDE ≌ △CDF(AAS)
∴DE=DF已知:△ABC中,AB=AC,D是BC边上的中点,DF⊥AC于F DE ⊥ AB 于E .
求证:DE=DF. 方法二:连结AD .
∵AB=AC,BD=DC(已知)
∴AD是∠BAC的平分线。
(等腰三角形三线合一)
又∵DE⊥AB DF⊥AC
∴ DE= DF
(角平分线上的点到这个
角的两边距离相等)
拓展
(1)若上题中DE、DF分别是AB、AC上的中线, DE=DF还成立吗?
(2)若DE、DF分别是∠ADB、∠ADC的平分线,DE=DF还成立吗?
由此你能得出什么结论?1、本节主要教学知识是等腰三角形的两个性质。2、本节课学习了数学思想及方法:分类讨论和一题多解,方程思想3、证明角相等的方法:
(1)根据三角形全等;(2)根据角的平分线性质的逆命题
(3)等边对等角
3、等腰三角形的一个角为75°,则它的另外两个角的度数是10或1175°30°或52.5°52.5°剪一剪 如图,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC是什么三角形?
想一想
刚才剪出的等腰三角形是轴对称图形吗?若是,它的对称轴是什么? 把剪出的△ABC沿着折痕AD折叠,找出重合的线段和角.找一找 猜一猜 等腰三角形除了两腰相等外,你还能发现它的其他性质吗?AB=ACAD=ADBD=CD∠B= ∠C∠ADB=∠ADC∠BAD=∠CAD性质1、等腰三角形的两个底角相等求证:∠B =∠C 已知: △ABC 中,AB=AC证明:作底边BC边上的中线AD
在△ABD与△ACD中:
AB=AC(已知)
BD=DC(已作)
AD=AD(公共边)
∴△ABD≌△ACD(SSS)
∴∠B=∠C(全等三角形对应角相等)证明:作顶角∠BAC的平分线AD
∵AD平分∠BAC
∴∠1=∠2
在△ABD与△ACD中
AB=AC(已知)
∠1=∠2(已证)
AD=AD(公共边)
∴ △ABD ≌ △ACD(SAS)
∴ ∠B=∠C
证明:作底边BC的高AD。
∵AD⊥BC
∴ ∠ADB =∠ADC=90°
在Rt△ABD与Rt△ACD中
AB=AC(已知)
AD=AD(公共边)
∴ Rt △ABD ≌ Rt △ACD
∴ ∠B=∠C议一议:说说为什么在添加辅助线时,作顶角平分线,底边中线,底边高都能使分成的两个三角形全等?性质1、等腰三角形的两个底角相等由△ABD ≌ △ACD,你还能得出什么结论?性质2 等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合(简称三线合一) 已知:△ABC中,AB=AC、BD平分∠ABC。
能否推出BD⊥AC、DA=DC吗?典型例题 如图,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD.
求△ABC各角的度数.提示:1、图中有几个等腰三角形?
2、可以得到哪些角相等?
3、若设∠A= x,你还能能用 x表示哪些角?解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠3, ∠A =∠1(等边对等角).
设∠A = x,则∠3= ∠A + ∠1=2x
∴∠ABC=∠C=∠3=2x
∵ ∠A+ ∠ABC+∠C = 180°
∴ x+2x+2x= 180°
解得:x=36°
∴ ∠A =36° ∴∠ABC=∠C=72° 已知:△ABC中,AB=AC,D是BC边上的中点,DF⊥AC于F DE ⊥ AB 于E .
求证:DE=DF. 证明: ∵DE⊥AB,DF⊥AC(已知)
∴∠BED=∠CFD
又∵D是BC中点(已知)
∴BD=DC
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
在△DBE与△DCF中
∠DEB=∠DFC(已证)
∠B=∠C(已证)
BD=DC(已证)
∴ △BDE ≌ △CDF(AAS)
∴DE=DF已知:△ABC中,AB=AC,D是BC边上的中点,DF⊥AC于F DE ⊥ AB 于E .
求证:DE=DF. 方法二:连结AD .
∵AB=AC,BD=DC(已知)
∴AD是∠BAC的平分线。
(等腰三角形三线合一)
又∵DE⊥AB DF⊥AC
∴ DE= DF
(角平分线上的点到这个
角的两边距离相等)
拓展
(1)若上题中DE、DF分别是AB、AC上的中线, DE=DF还成立吗?
(2)若DE、DF分别是∠ADB、∠ADC的平分线,DE=DF还成立吗?
由此你能得出什么结论?1、本节主要教学知识是等腰三角形的两个性质。2、本节课学习了数学思想及方法:分类讨论和一题多解,方程思想3、证明角相等的方法:
(1)根据三角形全等;(2)根据角的平分线性质的逆命题
(3)等边对等角
