数学 教学设计:“两个变量的线性相关(第三课时)”
文档属性
| 名称 | 数学 教学设计:“两个变量的线性相关(第三课时)” |

|
|
| 格式 | rar | ||
| 文件大小 | 292.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-10-20 00:00:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
数学:“两个变量的线性相关(第三课时)”教学设计
——最小二乘法求线性回归方程
一、内容和内容解析
本节课的主要内容为用最小二乘法思想求线性回归方程.
本节课内容作为上节课线性回归方程探究的知识发展,在知识上有很强的联系,所以,核心概念还是回归直线.在“经历用不同估算方法描述两个变量线性相关关系”的过程后,解决好用数学方法刻画“从整体上看,各点与此直线的距离最小”,让学生在此基础上了解更为科学的数据处理方式——最小二乘法,有助于更好的理解核心概念“回归直线”,并最终体现回归方法的应用价值.
就统计学科而言,对不同的数据处理方法进行“优劣评价”是“假设检验”的萌芽,而后者是统计学学科研究的另一重要领域.了解“最小二乘法思想”,比较各种“估算方法”,体会它的相对科学性,既是统计学教学发展的需要,又是“在体会此思想的过程中促进了学生对核心概念的进一步理解”的需要.“最小二乘法思想”作为本节课的核心思想,由此得以体现,而回归思想和贯穿统计学科中的随机思想,也在本节课中需有所渗透.
所以,在内容重点的侧重上,本节课与上节课有较大的区别:上节课侧重于估算方法设计,在不同的数据处理过程中,体会回归直线作为变量相关关系代表这一概念特征;本节课侧重于估算方法评价与实际应用,在评价中使学生体会核心思想,理解核心概念.
考虑到本节课的教学侧重点与新课程标准的要求,对线性回归方程系数的计算公式,可直接给出.由于公式的复杂性,一方面,既要通过教学设计合理体现知识发生过程,不搞“割裂”;另一方面,要充分利用计算机或计算器,简化繁琐的求解系数过程,简化过于形式化的证明说理过程.
基于上述内容分析,确定本节课的教学重点为知道最小二乘法思想,并能根据给出的线性回归方程的系数公式建立线性回归方程.
二、目标和目标解析
本节课要求学生了解最小二乘法思想,掌握根据给出的线性回归方程系数公式建立线性回归方程,理解线性回归方程概念和回归思想,在以上过程中体会随机思想:
1.能用数学符号刻画出“从整体上看,各点与此直线的点的偏差”的表达方式;
2.通过减少样本点个数,经历对表达式的展开,把“偏差最小”简化为“二次多项式”最小值问题,通过逻辑推理,使学生接受最小二乘法思想,体会到它的科学性,在此过程中了解最小二乘法思想;
3.能结合具体案例,经历数据处理步骤,根据回归方程系数公式建立回归方程;
4.通过改变同一问题下样本点的选择进而对照回归方程的差异,体会随机思想;
5.利用回归方程预测,体现用“确定关系研究相关关系”的回归思想.
三、教学问题诊断分析
在经历用不同估算方法描述两个变量线性相关的过程后,在学生现有知识能力范围内,如何选择一个最优方法,成为知识发展的逻辑必然.
“最小二乘法”作为经典的回归方程估算方法:通过用数学方法刻画“从整体上看,各点与此直线的距离最小”这一直观的几何描述,并采取合适的数学处理方法,最终获得回归直线,对学生认可统计估算的科学性有很大的帮助.
基于此,如何把“从整体上看,各点与此直线的距离最小”用合适的代数符号刻画并化简,化几何问题为代数问题,是顺利了解“最小二乘法”思想的前提;而如何化简复杂的代数表达式,学生缺乏处理的经验,在计算能力的要求上也较高.要了解“最小二乘法思想”,接受“由系数公式得到的线性方程”为回归方程,理解此方程可作为两个具有线性相关关系变量的代表这一回归直线概念本质,并体现相对于其他估算方法的优越性,又必须要求对给出的系数公式来源进行一定的说理.
知识发展的要求与学生能力和经验的欠缺成为本节课将会遇到的最大矛盾.教学中,要防止两种倾向:一是直接套用回归系数公式求解回归方程而回避说理过程;二是过多纠缠于数学刻画过程,甚至在课堂内花大量时间对回归系数公式进行证明说理.这两种倾向,都脱离了实际情况,前者忽略了“最小二乘法思想”,迷失了本节课的教学目标;后者则人为地拔高了教材要求,脱离了本节课教学要求.
所以,本节课的教学难点是:如何通过数学方法刻画“从整体上看,各点与此直线的距离最小”并在此过程中了解最小二乘法思想.回归方程中的斜率b和截距a的计算公式,用计算器求出线性回归方程.通过大量的回归直线比较分析,体会回归思想和随机思想.
四、教学支持条件分析
本节课需要运用回归系数公式求解回归直线,此过程要进行大量的运算,需要科学计算器减少繁琐的计算(本案使用的计算器型号为卡西欧fx-991ES).在后续例题的解决过程中,还需借助Excle软件,因此需要多媒体电脑展示设备支持.
五、教学过程设计
(一)课题引入
引言:我们知道,通过散点图可以判断两个变量之间是否具有“正相关”或“负相关”,但这只是一个定性的判断,更多的时候,我们需要的是定量的刻画.
我们从“人体的脂肪百分比与年龄”的相关关系的研究中知道,在年龄确定后,人体的脂肪百分比并不是惟一确定的.人们感兴趣的是,在知道年龄后,能否知道人体的脂肪百分比大约是多少?因此,若能找到一个函数模型(比如一次函数),用这个函数模型计算出来的函数值,可以作为人体的脂肪百分比的的近似值,并且这个近似值还具有一定的精确度,那么我们就能根据人们的年龄对人体的脂肪百分比作出预测.
【问题1】下列两个散点图中,两个变量之间是否具有线性相关关系?理由呢?是正相关还是负相关?
设计意图:回顾上节课所学内容,使学生的思想、知识和心理能较快地进入本节课课堂学习的状态.
师生活动:学生回答,图1没有线性相关关系,图2有线性相关关系,因为图1中的所有点都落在某一直线的附近.通过问题,使学生回忆前2节课核心概念:线性相关关系、正相关、负相关等,为后续学习打基础.
(二)本节课的新知识
【问题2】通过上一节课的学习,我们认为以“偏差”最小的直线作为回归直线比较恰当,那你能用代数式来刻画“从整体上看,各点与此直线的偏差最小”吗?
设计意图:几何问题代数化,为下一步探究作好准备,经历“几何直观”转化为“代数表达”过程,为引出“最小二乘法”作准备.
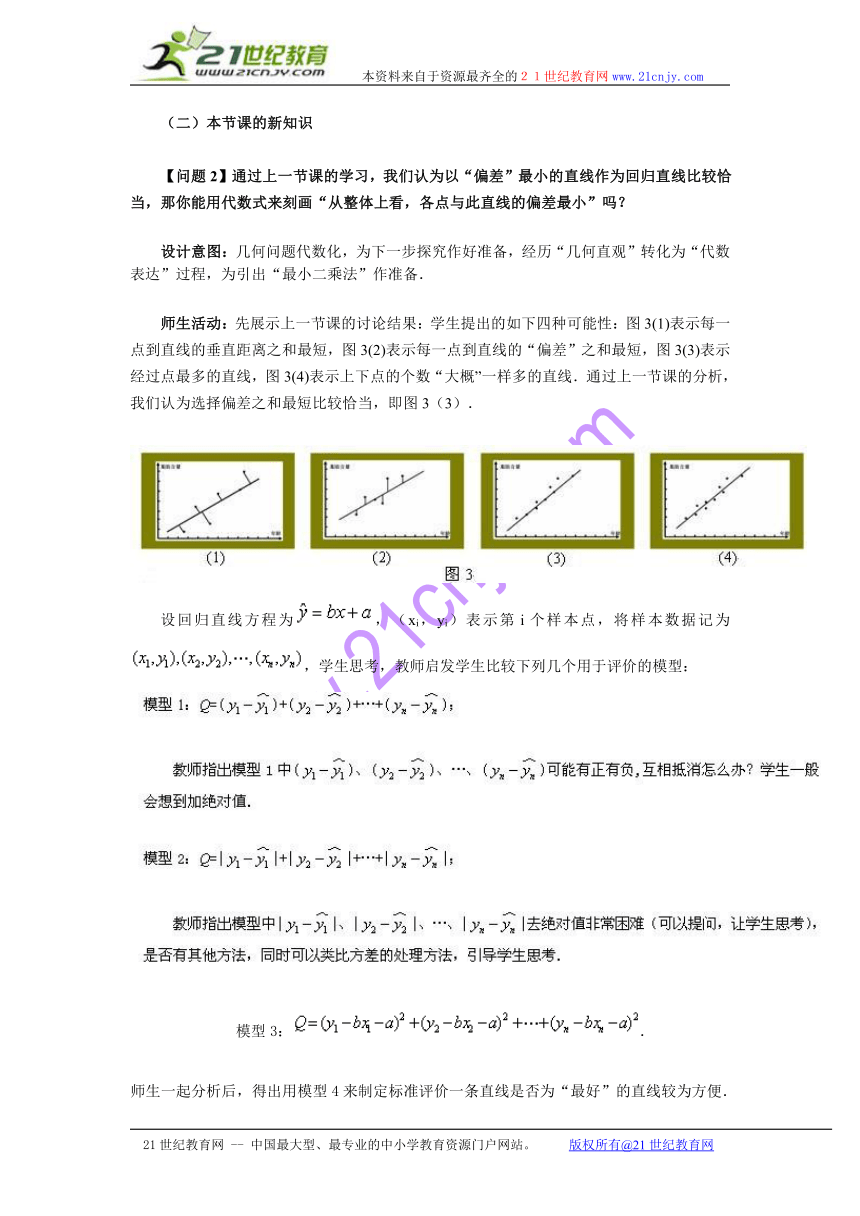
师生活动:先展示上一节课的讨论结果:学生提出的如下四种可能性:图3(1)表示每一点到直线的垂直距离之和最短,图3(2)表示每一点到直线的“偏差”之和最短,图3(3)表示经过点最多的直线,图3(4)表示上下点的个数“大概”一样多的直线.通过上一节课的分析,我们认为选择偏差之和最短比较恰当,即图3(3).
设回归直线方程为,(xi,yi)表示第i个样本点,将样本数据记为,学生思考,教师启发学生比较下列几个用于评价的模型:
模型3:.
师生一起分析后,得出用模型4来制定标准评价一条直线是否为“最好”的直线较为方便.
Q=(y1-bx1-a)2+(y2-bx2-a)2+…+(yn-bxn-a)2=
【问题3】通过对问题2的分析,我们知道了用Q=最小来表示偏差最小,那么在这个式子中,当样本点的坐标(xi,yi)确定时,a,b等于多少,Q能取到最小值呢?
设计意图:体会最小二乘法思想,不经历公式化简无法真正理解其意义,而直接从n个点的公式化简,教学要求、教学时间、学生能力都没达到这个高度.因而由具体到抽象,由特殊到一般,将是学生顺利完成这一认知过程的一般性原则.通过这个问题,让学生了解这个式子的结构,为后续的学习打下基础,同时渗透最小值的思想
师生活动:偏差最小从本质上来说是最小,为了处理方便,我们采用n个偏差的平方和Q=(y1-bx1-a)2+(y2-bx2-a)2+…+(yn-bxn-a)2表示n个点与相应直线在整体上的接近程度:记Q=(向学生说明的意义).通过化简,得到的其实是关于a、b的二元二次函数求最值的问题,一定存在这样的a、b,使Q取到最小值.
(1)在此基础上,视为的二次函数时,可求出使Q为最小值时的的值的线性回归方程系数公式:
(2)教师指出,称为样本点的中心,可以证明回归直线一定过样本点的中心,所以可得上述方法求回归直线的方法,
是使得样本数据的点到它的距离的平方和最小,由于平方又叫二乘方,所以这种使距离平方最小的方法,叫做最小二乘法.
【问题4】线性回归方程为何不记为?你能说明对于确定的,根据计算出的的意义吗?
设计意图:使学生理解线性回归方程的真正意义与作用,明确只是的一个估计值.
师生活动:学生思考,教师帮助学生理解线性回归方程的意义与作用.
【问题5】这个公式不要求记忆,但要会运用这个公式进行运算,那么,要求,的值,你会按怎样的顺序求呢?
设计意图:公式不要求推导,又不要求记忆,学生对这个公式缺少感性的认识,通过这个问题,使学生从感性的层次上对公式有所了解.
师生活动:由于这个公式比较复杂,因此在运用这个公式求,时,必须要有条理,先求什么,再求什么,比如,我们可以按照、n、、、、顺序来求,再代入公式.我们一般可以列如下表格进行分布计算:
(三)知识深化:
【问题6】你能根据表一所提供的样本数据,求出线性回归方程吗?
表一:人体的脂肪百分比和年龄
设计意图:公式形式化程度高、表达复杂,通过分解计算,可加深对公式结构的理解.同时,通过例题,反映数据处理的繁杂性,体现计算器处理的优越性.
师生活动:步骤一,可让学生观察公式,充分讨论,通过计算:n、、、、五个数据带入回归方程公式得到线性回归方程,体会求线性回归方程的原理与方法.
由此可以得到回归直线方程为:
步骤二,教师分析求线性回归方程的基本步骤,然后带领学生用卡西欧FX-991 ES计算器求出线性回归方程并画出回归直线,教师可协同学生,对计算器操作方式提供示范,师生共同完成.(操作方法见学生学案)
【问题7】利用计算器,根据表二数据,请同学们独立解决求出表中两变量的回归方程:
表二:
设计意图:让学生独立体验运用计算器求回归直线方程,在重复求解回归直线的过程中,使学生掌握利用计算器求回归直线的操作方法,了解计算机处理方法.教师利用Excle软件,示范操作,并适时给出回归直线答案,检测正确与否.
师生活动:
活动一,学生独立运用计算器求回归直线方程,对于不会操作的学生,教师给予必要的指导.
活动二,在引入的过程中,很多同学考虑到经过的点最多的直线,现在求出了回归直线方程,请同学计算它经过了几个样本点?
活动三,学生完成之后,教师利用Excle软件在屏幕上演示,指出Excle软件也能帮助我们求出回归直线方程.(操作过程见学生学案).得到回归直线为:=0.4767x+4.9476
活动四,年龄为62岁的人脂肪含量是多少?
【问题8】利用计算器,根据表三数据,请同学们独立解决求出表中两变量的回归方程:
表三:
设计意图:让学生独立体验运用计算器求回归直线方程,在重复求解回归直线的过程中,使学生掌握利用计算器求回归直线的操作方法,同时为下一个问题服务.
师生活动:学生独立运用计算器求回归直线方程,对于还不会操作的学生,教师给予必要的指导.使学生能熟练运用计算器求回归方程.求出回归直线方程为= 0.5765x - 0.4478
(教师运用excel分别求出问题8,问题9的回归直线方程后,并告诉学生,问题7,问题8的数据就是课本85页的数据(问题9)拆开而成的)
回归直线为:=0.6541x-4.5659
回归直线为:=0.4767x+4.9476
回归直线为:= 0.5765x - 0.4478
【问题9】同样问题背景,为什么回归直线不止一条?回归方程求出后,变量间的相关关系是否就转变成确定关系?
设计意图:明确样本的选择影响回归直线方程,体现统计的随机思想.同时,明确其揭示的是相关关系而非函数的确定关系,而且最小二乘法只是某一标准下的一种数据处理方法,使学生更全面的理解回归直线这一核心概念.
师生活动:回归方程求出后,变量间的相关关系并没有转变为确定关系,只是用确定的函数关系来研究不确定的相关关系.回归直线方程由数据唯一决定,提供的数据不同,回归直线方程当然不同,同时回归直线方程又能反映数据的本质.
案例1:此检验结果仅对本次标本有意义
案例2:卖出热茶的杯数与当天气温的关系
下表是某小卖部6天卖出热茶的杯数与当天气温的对比表(用计算器直接求回归直线):
(1)求回归方程;
(2)按照回归方程,计算温度为10度时销售杯数.为什么与表中不同?如果某天的气温是-5℃时,预测这天小卖部卖出热茶的杯数.
让学生完整经历求回归直线的过程.其中第2问,让学生体会到即使是相比下“最优”的所获得的回归直线,也存在着一定的误差,从中体会无论方法的优劣,统计学中随机性无法避免.而在预测值的计算中,体现了回归直线的应用价值.
通过对以上两个案例的分析,说明事件、样本数据、回归直线方程三者关系:
1.数据采样本身就具有随机性,同样23岁的人,脂肪含量可能9.5%,也有可能30%,这种误差我们称之为随机误差,随机误差是不可避免的.
2.回归分析是寻找相关关系中非确定关系中的某种确定性,虽然一个数据具有随机误差,但总体还是具有某种确定的关系.
3.在数据采样都符合统计要求的情况下,取三个回归直线方程中的任意一个都是合理的,不存在哪条最合适的问题,但一般情况下,选择数据多一些的比较合理.
因此,事件、样本数据、回归直线方程三者具有如下的关系:
(四)小结:
【问题10】请同学们回顾一下我们怎样求出回归直线方程?事件、样本数据与回归直线三者之间有怎样的关系?
设计意图:培养学生反思的习惯,鼓励学生对研究的问题进行质疑和概括.
师生活动:
1.求样本数据的线性回归方程的方法
(1)直接运用公式
(2)借助计算器或计算机(使用方法见学案)
2.样本数据与回归直线的关系(如图6)
六、目标检测设计
朱老师在某网站的论坛上发了一个帖子“新课程需要怎样的教学方式”,引起了广泛的关注.现统计发贴天数与点击次数如下:
(1)求出关于的回归直线方程.
(2)根据求出的回归直线方程,预测第20天的点击次数.
设计意图:通过本练习的解决,让学生巩固熟悉回归方程求解的过程.并体会运用回归方程进行预测.
《最小二乘法求线性回归方程》学生课堂学案
姓名:
1.你能根据表一所提供的样本数据,求出线性回归方程吗?
人体的脂肪百分比和年龄
数据A:
答案: 回归直线方程为:
2.利用计算器,根据表二数据,请同学们独立解决求出表中两变量的回归方程:
数据B:
数据记录:
答案: 回归直线方程为:
3.利用计算器,根据表三数据,请同学们独立解决求出表中两变量的回归方程:
数据C:
答案: 回归直线方程为:
4.下表是某小卖部6天卖出热茶的杯数与当天气温的对比表(用计算器直接求回归直线):
(1)画散点图;(坐标在下一页) (2)求回归方程,并在图上画出直线;
(3)按照回归方程,计算温度为10度时销售杯数.如果某天的气温是-5℃时,预测这天小卖部卖出热茶的杯数.
附录1:
1.系数公式:
2.excel表格操作方法:
(1)输入数据表(纵向);
(2)选中数据表格,在菜单中选定“插入”中的“图表”,弹出“图表类型”对话框,选择“XY散点图”;单击“完成”按钮.
(3)选中散点图,在菜单中选定“图表”中的“添加趋势线”选项,弹出“添加趋势线”对话框;
(4)单击“类型”标签,选定“趋势预测/回归分析类型”中的“线性”选项,单击“确定”按钮,得到回归直线.
(5)双击回归直线,弹出“趋势线格式”对话框,单击“选项”标签,选定“显示公式”,最后单击“确定”按钮,得到回归直线的回归方程.
3.计算器的使用:
2010-05-05
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
数学:“两个变量的线性相关(第三课时)”教学设计
——最小二乘法求线性回归方程
一、内容和内容解析
本节课的主要内容为用最小二乘法思想求线性回归方程.
本节课内容作为上节课线性回归方程探究的知识发展,在知识上有很强的联系,所以,核心概念还是回归直线.在“经历用不同估算方法描述两个变量线性相关关系”的过程后,解决好用数学方法刻画“从整体上看,各点与此直线的距离最小”,让学生在此基础上了解更为科学的数据处理方式——最小二乘法,有助于更好的理解核心概念“回归直线”,并最终体现回归方法的应用价值.
就统计学科而言,对不同的数据处理方法进行“优劣评价”是“假设检验”的萌芽,而后者是统计学学科研究的另一重要领域.了解“最小二乘法思想”,比较各种“估算方法”,体会它的相对科学性,既是统计学教学发展的需要,又是“在体会此思想的过程中促进了学生对核心概念的进一步理解”的需要.“最小二乘法思想”作为本节课的核心思想,由此得以体现,而回归思想和贯穿统计学科中的随机思想,也在本节课中需有所渗透.
所以,在内容重点的侧重上,本节课与上节课有较大的区别:上节课侧重于估算方法设计,在不同的数据处理过程中,体会回归直线作为变量相关关系代表这一概念特征;本节课侧重于估算方法评价与实际应用,在评价中使学生体会核心思想,理解核心概念.
考虑到本节课的教学侧重点与新课程标准的要求,对线性回归方程系数的计算公式,可直接给出.由于公式的复杂性,一方面,既要通过教学设计合理体现知识发生过程,不搞“割裂”;另一方面,要充分利用计算机或计算器,简化繁琐的求解系数过程,简化过于形式化的证明说理过程.
基于上述内容分析,确定本节课的教学重点为知道最小二乘法思想,并能根据给出的线性回归方程的系数公式建立线性回归方程.
二、目标和目标解析
本节课要求学生了解最小二乘法思想,掌握根据给出的线性回归方程系数公式建立线性回归方程,理解线性回归方程概念和回归思想,在以上过程中体会随机思想:
1.能用数学符号刻画出“从整体上看,各点与此直线的点的偏差”的表达方式;
2.通过减少样本点个数,经历对表达式的展开,把“偏差最小”简化为“二次多项式”最小值问题,通过逻辑推理,使学生接受最小二乘法思想,体会到它的科学性,在此过程中了解最小二乘法思想;
3.能结合具体案例,经历数据处理步骤,根据回归方程系数公式建立回归方程;
4.通过改变同一问题下样本点的选择进而对照回归方程的差异,体会随机思想;
5.利用回归方程预测,体现用“确定关系研究相关关系”的回归思想.
三、教学问题诊断分析
在经历用不同估算方法描述两个变量线性相关的过程后,在学生现有知识能力范围内,如何选择一个最优方法,成为知识发展的逻辑必然.
“最小二乘法”作为经典的回归方程估算方法:通过用数学方法刻画“从整体上看,各点与此直线的距离最小”这一直观的几何描述,并采取合适的数学处理方法,最终获得回归直线,对学生认可统计估算的科学性有很大的帮助.
基于此,如何把“从整体上看,各点与此直线的距离最小”用合适的代数符号刻画并化简,化几何问题为代数问题,是顺利了解“最小二乘法”思想的前提;而如何化简复杂的代数表达式,学生缺乏处理的经验,在计算能力的要求上也较高.要了解“最小二乘法思想”,接受“由系数公式得到的线性方程”为回归方程,理解此方程可作为两个具有线性相关关系变量的代表这一回归直线概念本质,并体现相对于其他估算方法的优越性,又必须要求对给出的系数公式来源进行一定的说理.
知识发展的要求与学生能力和经验的欠缺成为本节课将会遇到的最大矛盾.教学中,要防止两种倾向:一是直接套用回归系数公式求解回归方程而回避说理过程;二是过多纠缠于数学刻画过程,甚至在课堂内花大量时间对回归系数公式进行证明说理.这两种倾向,都脱离了实际情况,前者忽略了“最小二乘法思想”,迷失了本节课的教学目标;后者则人为地拔高了教材要求,脱离了本节课教学要求.
所以,本节课的教学难点是:如何通过数学方法刻画“从整体上看,各点与此直线的距离最小”并在此过程中了解最小二乘法思想.回归方程中的斜率b和截距a的计算公式,用计算器求出线性回归方程.通过大量的回归直线比较分析,体会回归思想和随机思想.
四、教学支持条件分析
本节课需要运用回归系数公式求解回归直线,此过程要进行大量的运算,需要科学计算器减少繁琐的计算(本案使用的计算器型号为卡西欧fx-991ES).在后续例题的解决过程中,还需借助Excle软件,因此需要多媒体电脑展示设备支持.
五、教学过程设计
(一)课题引入
引言:我们知道,通过散点图可以判断两个变量之间是否具有“正相关”或“负相关”,但这只是一个定性的判断,更多的时候,我们需要的是定量的刻画.
我们从“人体的脂肪百分比与年龄”的相关关系的研究中知道,在年龄确定后,人体的脂肪百分比并不是惟一确定的.人们感兴趣的是,在知道年龄后,能否知道人体的脂肪百分比大约是多少?因此,若能找到一个函数模型(比如一次函数),用这个函数模型计算出来的函数值,可以作为人体的脂肪百分比的的近似值,并且这个近似值还具有一定的精确度,那么我们就能根据人们的年龄对人体的脂肪百分比作出预测.
【问题1】下列两个散点图中,两个变量之间是否具有线性相关关系?理由呢?是正相关还是负相关?
设计意图:回顾上节课所学内容,使学生的思想、知识和心理能较快地进入本节课课堂学习的状态.
师生活动:学生回答,图1没有线性相关关系,图2有线性相关关系,因为图1中的所有点都落在某一直线的附近.通过问题,使学生回忆前2节课核心概念:线性相关关系、正相关、负相关等,为后续学习打基础.
(二)本节课的新知识
【问题2】通过上一节课的学习,我们认为以“偏差”最小的直线作为回归直线比较恰当,那你能用代数式来刻画“从整体上看,各点与此直线的偏差最小”吗?
设计意图:几何问题代数化,为下一步探究作好准备,经历“几何直观”转化为“代数表达”过程,为引出“最小二乘法”作准备.
师生活动:先展示上一节课的讨论结果:学生提出的如下四种可能性:图3(1)表示每一点到直线的垂直距离之和最短,图3(2)表示每一点到直线的“偏差”之和最短,图3(3)表示经过点最多的直线,图3(4)表示上下点的个数“大概”一样多的直线.通过上一节课的分析,我们认为选择偏差之和最短比较恰当,即图3(3).
设回归直线方程为,(xi,yi)表示第i个样本点,将样本数据记为,学生思考,教师启发学生比较下列几个用于评价的模型:
模型3:.
师生一起分析后,得出用模型4来制定标准评价一条直线是否为“最好”的直线较为方便.
Q=(y1-bx1-a)2+(y2-bx2-a)2+…+(yn-bxn-a)2=
【问题3】通过对问题2的分析,我们知道了用Q=最小来表示偏差最小,那么在这个式子中,当样本点的坐标(xi,yi)确定时,a,b等于多少,Q能取到最小值呢?
设计意图:体会最小二乘法思想,不经历公式化简无法真正理解其意义,而直接从n个点的公式化简,教学要求、教学时间、学生能力都没达到这个高度.因而由具体到抽象,由特殊到一般,将是学生顺利完成这一认知过程的一般性原则.通过这个问题,让学生了解这个式子的结构,为后续的学习打下基础,同时渗透最小值的思想
师生活动:偏差最小从本质上来说是最小,为了处理方便,我们采用n个偏差的平方和Q=(y1-bx1-a)2+(y2-bx2-a)2+…+(yn-bxn-a)2表示n个点与相应直线在整体上的接近程度:记Q=(向学生说明的意义).通过化简,得到的其实是关于a、b的二元二次函数求最值的问题,一定存在这样的a、b,使Q取到最小值.
(1)在此基础上,视为的二次函数时,可求出使Q为最小值时的的值的线性回归方程系数公式:
(2)教师指出,称为样本点的中心,可以证明回归直线一定过样本点的中心,所以可得上述方法求回归直线的方法,
是使得样本数据的点到它的距离的平方和最小,由于平方又叫二乘方,所以这种使距离平方最小的方法,叫做最小二乘法.
【问题4】线性回归方程为何不记为?你能说明对于确定的,根据计算出的的意义吗?
设计意图:使学生理解线性回归方程的真正意义与作用,明确只是的一个估计值.
师生活动:学生思考,教师帮助学生理解线性回归方程的意义与作用.
【问题5】这个公式不要求记忆,但要会运用这个公式进行运算,那么,要求,的值,你会按怎样的顺序求呢?
设计意图:公式不要求推导,又不要求记忆,学生对这个公式缺少感性的认识,通过这个问题,使学生从感性的层次上对公式有所了解.
师生活动:由于这个公式比较复杂,因此在运用这个公式求,时,必须要有条理,先求什么,再求什么,比如,我们可以按照、n、、、、顺序来求,再代入公式.我们一般可以列如下表格进行分布计算:
(三)知识深化:
【问题6】你能根据表一所提供的样本数据,求出线性回归方程吗?
表一:人体的脂肪百分比和年龄
设计意图:公式形式化程度高、表达复杂,通过分解计算,可加深对公式结构的理解.同时,通过例题,反映数据处理的繁杂性,体现计算器处理的优越性.
师生活动:步骤一,可让学生观察公式,充分讨论,通过计算:n、、、、五个数据带入回归方程公式得到线性回归方程,体会求线性回归方程的原理与方法.
由此可以得到回归直线方程为:
步骤二,教师分析求线性回归方程的基本步骤,然后带领学生用卡西欧FX-991 ES计算器求出线性回归方程并画出回归直线,教师可协同学生,对计算器操作方式提供示范,师生共同完成.(操作方法见学生学案)
【问题7】利用计算器,根据表二数据,请同学们独立解决求出表中两变量的回归方程:
表二:
设计意图:让学生独立体验运用计算器求回归直线方程,在重复求解回归直线的过程中,使学生掌握利用计算器求回归直线的操作方法,了解计算机处理方法.教师利用Excle软件,示范操作,并适时给出回归直线答案,检测正确与否.
师生活动:
活动一,学生独立运用计算器求回归直线方程,对于不会操作的学生,教师给予必要的指导.
活动二,在引入的过程中,很多同学考虑到经过的点最多的直线,现在求出了回归直线方程,请同学计算它经过了几个样本点?
活动三,学生完成之后,教师利用Excle软件在屏幕上演示,指出Excle软件也能帮助我们求出回归直线方程.(操作过程见学生学案).得到回归直线为:=0.4767x+4.9476
活动四,年龄为62岁的人脂肪含量是多少?
【问题8】利用计算器,根据表三数据,请同学们独立解决求出表中两变量的回归方程:
表三:
设计意图:让学生独立体验运用计算器求回归直线方程,在重复求解回归直线的过程中,使学生掌握利用计算器求回归直线的操作方法,同时为下一个问题服务.
师生活动:学生独立运用计算器求回归直线方程,对于还不会操作的学生,教师给予必要的指导.使学生能熟练运用计算器求回归方程.求出回归直线方程为= 0.5765x - 0.4478
(教师运用excel分别求出问题8,问题9的回归直线方程后,并告诉学生,问题7,问题8的数据就是课本85页的数据(问题9)拆开而成的)
回归直线为:=0.6541x-4.5659
回归直线为:=0.4767x+4.9476
回归直线为:= 0.5765x - 0.4478
【问题9】同样问题背景,为什么回归直线不止一条?回归方程求出后,变量间的相关关系是否就转变成确定关系?
设计意图:明确样本的选择影响回归直线方程,体现统计的随机思想.同时,明确其揭示的是相关关系而非函数的确定关系,而且最小二乘法只是某一标准下的一种数据处理方法,使学生更全面的理解回归直线这一核心概念.
师生活动:回归方程求出后,变量间的相关关系并没有转变为确定关系,只是用确定的函数关系来研究不确定的相关关系.回归直线方程由数据唯一决定,提供的数据不同,回归直线方程当然不同,同时回归直线方程又能反映数据的本质.
案例1:此检验结果仅对本次标本有意义
案例2:卖出热茶的杯数与当天气温的关系
下表是某小卖部6天卖出热茶的杯数与当天气温的对比表(用计算器直接求回归直线):
(1)求回归方程;
(2)按照回归方程,计算温度为10度时销售杯数.为什么与表中不同?如果某天的气温是-5℃时,预测这天小卖部卖出热茶的杯数.
让学生完整经历求回归直线的过程.其中第2问,让学生体会到即使是相比下“最优”的所获得的回归直线,也存在着一定的误差,从中体会无论方法的优劣,统计学中随机性无法避免.而在预测值的计算中,体现了回归直线的应用价值.
通过对以上两个案例的分析,说明事件、样本数据、回归直线方程三者关系:
1.数据采样本身就具有随机性,同样23岁的人,脂肪含量可能9.5%,也有可能30%,这种误差我们称之为随机误差,随机误差是不可避免的.
2.回归分析是寻找相关关系中非确定关系中的某种确定性,虽然一个数据具有随机误差,但总体还是具有某种确定的关系.
3.在数据采样都符合统计要求的情况下,取三个回归直线方程中的任意一个都是合理的,不存在哪条最合适的问题,但一般情况下,选择数据多一些的比较合理.
因此,事件、样本数据、回归直线方程三者具有如下的关系:
(四)小结:
【问题10】请同学们回顾一下我们怎样求出回归直线方程?事件、样本数据与回归直线三者之间有怎样的关系?
设计意图:培养学生反思的习惯,鼓励学生对研究的问题进行质疑和概括.
师生活动:
1.求样本数据的线性回归方程的方法
(1)直接运用公式
(2)借助计算器或计算机(使用方法见学案)
2.样本数据与回归直线的关系(如图6)
六、目标检测设计
朱老师在某网站的论坛上发了一个帖子“新课程需要怎样的教学方式”,引起了广泛的关注.现统计发贴天数与点击次数如下:
(1)求出关于的回归直线方程.
(2)根据求出的回归直线方程,预测第20天的点击次数.
设计意图:通过本练习的解决,让学生巩固熟悉回归方程求解的过程.并体会运用回归方程进行预测.
《最小二乘法求线性回归方程》学生课堂学案
姓名:
1.你能根据表一所提供的样本数据,求出线性回归方程吗?
人体的脂肪百分比和年龄
数据A:
答案: 回归直线方程为:
2.利用计算器,根据表二数据,请同学们独立解决求出表中两变量的回归方程:
数据B:
数据记录:
答案: 回归直线方程为:
3.利用计算器,根据表三数据,请同学们独立解决求出表中两变量的回归方程:
数据C:
答案: 回归直线方程为:
4.下表是某小卖部6天卖出热茶的杯数与当天气温的对比表(用计算器直接求回归直线):
(1)画散点图;(坐标在下一页) (2)求回归方程,并在图上画出直线;
(3)按照回归方程,计算温度为10度时销售杯数.如果某天的气温是-5℃时,预测这天小卖部卖出热茶的杯数.
附录1:
1.系数公式:
2.excel表格操作方法:
(1)输入数据表(纵向);
(2)选中数据表格,在菜单中选定“插入”中的“图表”,弹出“图表类型”对话框,选择“XY散点图”;单击“完成”按钮.
(3)选中散点图,在菜单中选定“图表”中的“添加趋势线”选项,弹出“添加趋势线”对话框;
(4)单击“类型”标签,选定“趋势预测/回归分析类型”中的“线性”选项,单击“确定”按钮,得到回归直线.
(5)双击回归直线,弹出“趋势线格式”对话框,单击“选项”标签,选定“显示公式”,最后单击“确定”按钮,得到回归直线的回归方程.
3.计算器的使用:
2010-05-05
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
